אינפי 2 לתיכוניסטים תש"ע - שאלות ותשובות

$\lim_{n\rightarrow\infty}f_n$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחילת הדף את השורה הבאה:

== כותרת לשאלה ==

לכתוב מתחתיה את שאלתכם, וללחוץ על שמירה למטה מימין

ארכיון

ארכיון 1 - תרגיל 1 ו2

ארכיון 2 - תרגיל 3

ארכיון 3 - תרגיל 3

ארכיון 4 - תרגיל 4

ארכיון 5 - תרגיל 4,5

ארכיון 6 - תרגיל 6

ארכיון 7 - (מי עוקב)

ארכיון 8

ארכיון 9 - לקראת הבוחן

ארכיון 10 - פוסט בוחן

שאלות

שאלה

בתרגיל 2 סעיף a, צריך בכלל את העובדה שf יורדת? אי אפשר להניח בשלילה שהגבול הוא לא 0 ולכן קיים אפסילון כך שלכל x0 קיים x>x0 שעבורו מתקיים ש|fx| גדול שווה לאפסילון וכך להמשיך ולהגיע לסתירה?

עוד שאלה. מותר לי להשתמש בכל המשפטים על אינטגרלים רגילים, כמו למשל שאי שיוויון ברמת האינטגרל גורר אי שיוויון ברמת הפונקציה או שהאינטגרל בין a לX של 1*dx הוא X-a, גם באינטגרלים לא אמיתיים?

תשובה

ראינו בשיעור דוגמא לכך שהאינטגרל הלא אמיתי מתכנס אבל הפונקציה לא שואפת לאפס ואף לא חסומה (!) לכן בוודאי לא נצליח להוכיח את זה לפונקציה כללית.

אי שיוויון ברמת האינטגרל לא גורר אי שיוויון ברמת הפונקציה אלא להפך. אפשר להשתמש במשפטים רק כאשר הם נכונים. יש לזכור שהאינטגרל הלא אמיתי מוגדר כגבול של אינטרגלים אמיתיים. (לכן למשל אי שיווין ברמת הפונקציה יגרור אי שיוויון של כל האינטגרלים האמיתיים ולכן יגרור אי שיוויון חלש באינטגרל האינסופי).

אוקי. ואם יש לנו אינטגרל של 1 מa עד x. זה בעצם אינסוף, לא? לפי הגדרה זה שווה לאורך הקטע, ומכיוון שאורך הקטע הוא אינסופי - כך גם האינטגרל..

ומה לא בסדר עם ההוכחה שלי? איזה שלב לא נכון? הנחתי בשלילה שהגבול הוא לא 0 ואז קיים אפסילון כך שלכל x0 קיים x>x0 שעבורו |fx|>=E. (בתפקיד האפסילון - E). עכשיו, נפעיל אינטגרל על שני הצדדים ונשאיף אותו לאינסוף. נקבל שהאינטגרל הלא אמיתי של f(x) שואף גם הוא לאינסוף..

מa עד x זה אורך הקטע. מa עד אינסוף האינטגרל של 1 הוא אכן אינסוף (השטח של מלבן ברוחב 1 ואורך אינסופי הוא אינסוף

הבעייה עם "ההוכחה" היא שהיא לא הוכחה בכלל. הראת שיש אינסוף נקודות בהן הפונקציה גדולה מאפסילון. אז מה? לפונקציה יש "גבעות" (או בדוגמא שהראנו משולשים) שהגובה שלהם קבוע, אבל הרוחב הולך וקטן ולכן השטח הולך וקטן. הסכום האינסופי של השטחים האלה מתכנס.

עכשיו ראיתי עוד טעות שעשית. בעקבות אי השיויון במספר מסויים של נקודות הנחת שיש אי שיוויון ברמת האינטגרל, אבל זה אסור כמובן. צריך להראות שהפונקציה גדולה בגל מקום מאפסילון (וזה לא נכון)

תודה רבה :)

שאלה

בתרגיל 5, למה צריך את נוסחת בונה? אי אפשר פשוט לפצל את האינטגרל לאינטגרל ל"א מסוג 1 ול"א מסוג 2 ואז להוכיח עבור כל אחד בנפרד? (לפי מבחן ההשוואה+דיריכלה)

תשובה

אפשר, אבל הרעיון הוא להשתמש בנוסחאת בונה

פתרון לשאלת אתגר

נכון מאד

(קל יותר לומר שהפונקציה מוגדרת בקטע, ולכן חסומה על ידי הקצוות)

שאלה

איך הקבוצה של רוני יכולה לפתור את התרגיל עד יום שלישי?יש שם כמה דברים שלא למדנו.....

תשובה

אין שם דברים שלא למדתם, אם אני טועה אני אשמח לשמוע איזה תרגילים כוללים חומר שלא נלמד.

הדבר היחיד שלא תרגלתם הוא מבחן האינטגרל, שאין מה ללמוד אותו לצורך התרגיל, אני אצטט אותו:

תהי f פונקציה חיובית יורדת עבור 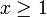$x \geq 1$ אזי

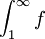$\int_1^{\infty}f$ מתכנס אם"ם הטור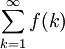 $\sum_{k=1}^{\infty}f(k)$

שאלה

לעתים נתונים לנו אינטגרלים לא אמיתיים שהם "משני הסוגים", כלומר בקצה אחד הם לא חסומים והקצה השני הוא אינסוף. כדי לקבוע התכנסות או התבדרות של אינטגרלים כאלה, האם אפשר להפעיל פשוט את מבחן ההשוואה על הפונציה כולה? או שיש לפצל אותו לשני אינטגרלים ואז לגבי כל אינטגרל לקבוע התכנסות או התבדרות? למשל בשאלה 6 בתרגיל 9. האם עלי לפצל את האינטגרל לסכום של שני אינטגרלים ואז לבדוק עבור כל אינטגרל הנפרד את ערכי אלפא שעבורם האינטגרל מתכנס, ואז לבדוק את ערכי האלפא שגורמים לשני האינטגרלים להתכנס? או שאני יכול לעבוד על אינטגרל הזה בתור יחידה אחת?

תשובה

מבחן ההשוואה הרגיל לא קשור בצד הגבול, ואם תעשה אותו עם פונקציה שמתכנסת בשני הצדדים גם הפונקציה שלך תתכנס בשני הצדדים.

מבחן ההשוואה הגבולי הוא לקיחת גבול (אינסוף או a) ולכן בכל מקרה צריך להפעיל אותו פעמיים גם אם תיקח את אותה פונקציה.

בכל אופן התשובה היא שצריך לפרק, אין באמת כזה דבר לעבוד כיחידה אחת.

בקשת דחייה

היי ארז. האם נוכל להגיש את התרגיל ביום שלישי? להרבה מאיתנו יש בגרות בתנ"ך ביום ראשון.