הבדלים בין גרסאות בדף "אלגוריתם ללכסון מטריצה"

גרסה מ־18:27, 29 בנובמבר 2011

תהי מטריצה A. נרצה לדעת האם היא לכסינה ומהי המטריצה המלכסנת שלה

תוכן עניינים

1 מציאת פולינום אופייני
2 מציאת הערכים העצמיים של המטריצה וריבויים האלגברי
3 מציאת המרחבים העצמיים של הערכים העצמיים
4 מציאת בסיסים למרחבים העצמיים
5 בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת

מציאת פולינום אופייני

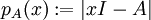$p_A(x):=\left|xI-A\right|$ .

מציאת הערכים העצמיים של המטריצה וריבויים האלגברי

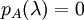$\lambda$ ערך עצמי של $A$ אם ורק אם $p_A(\lambda)=0$ .

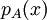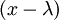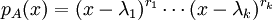לכל שורש $\lambda$ של $p_A(x)$ , נוציא מהפולינום גורם $(x-\lambda)$ , עד שנגיע למצב $p_A(x)=(x-\lambda_1)^{r_1}\cdots(x-\lambda_k)^{r_k}$ .

אם נותר בפולינום גורם שאינו מתפרק לגורמים לינאריים כאלה, אז המטריצה אינה לכסינה ואפשר לעצור כאן.

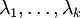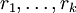$\lambda_1,\dots,\lambda_k$ הם הערכים העצמיים השונים של $A$ , ו $r_1,\dots,r_k$ הם הריבויים האלגבריים שלהם, בהתאמה.

מציאת המרחבים העצמיים של הערכים העצמיים

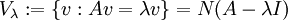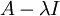לכל ערך עצמי $\lambda$ של $A$ , מחשבים את המרחב העצמי $V_\lambda:=\left\{v : Av=\lambda v\right\}=N(A-\lambda I)$ , אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה $A-\lambda I$ .

מוצאים בסיס עבור מרחב זה. אם בבסיס יש פחות איברים מהריבוי האלגברי של $\lambda$ , אז המטריצה אינה לכסינה ולא צריך להמשיך.

כל עוד יש מספיק וקטורים כמו בריבוי האלגברי, ממשיכים הלאה לערכים העצמיים הבאים. אם הצלחנו עבור כולם, מובטח שהמטריצה לכסינה, והמטריצה המלכסנת היא המטריצה שעמודותיה הם הוקטורים העצמיים בבסיסים שמצאנו.

מומלץ להיזכר במציאת בסיס למרחב האפס

מציאת בסיסים למרחבים העצמיים

ידוע מלינארית 1 כי בסיס למרחב האפס מורכב מהפתרונות הפונדומנטליים של המערכת ההומוגנית

בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת

אם סכום מימדי המרחבים העצמיים שווה למימד המרחב כולו (ניתן לגלות לפי מספר האיברים בבסיסים), אזי המטריצה לכסינה והמטריצה המלכסנת P היא המטריצה שעמודותיה הם הוקטורים מהבסיסים הנ"ל.

אחרת, המטריצה אינה לכסינה

@@ שורה 18: / שורה 18: @@
 הם הריבויים האלגבריים שלהם, בהתאמה.
-===מציאת מרחבים עצמיים של הערכים העצמיים===
+===מציאת המרחבים העצמיים של הערכים העצמיים===
-המרחב העצמי של ע"ע x מוגדר להיות:
+לכל ערך עצמי <math>\lambda</math> של <math>A</math>, מחשבים את המרחב העצמי
-::<math>V_x:=\{v|Av=xv\}</math>
+<math>V_\lambda:=\left\{v : Av=\lambda v\right\}=N(A-\lambda I)</math>,
+אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה <math>A-\lambda I</math>.
+מוצאים בסיס עבור מרחב זה. אם בבסיס יש פחות איברים מהריבוי האלגברי של <math>\lambda</math>,
+אז '''המטריצה אינה לכסינה''' ולא צריך להמשיך.
+כל עוד יש מספיק וקטורים כמו בריבוי האלגברי, ממשיכים הלאה לערכים העצמיים הבאים. אם הצלחנו עבור כולם, מובטח
+שהמטריצה לכסינה, והמטריצה המלכסנת היא המטריצה שעמודותיה הם הוקטורים העצמיים בבסיסים שמצאנו.
-קל להוכיח כי <math>V_x=N(A-xI)</math>. במילים, המרחב העצמי של ע"ע הוא אוסף הפתרונות של המערכת ההומוגנית המתאימה למטריצה A-xI.

הבדלים בין גרסאות בדף "אלגוריתם ללכסון מטריצה"

גרסה מ־18:27, 29 בנובמבר 2011

תוכן עניינים

מציאת פולינום אופייני

מציאת הערכים העצמיים של המטריצה וריבויים האלגברי

מציאת המרחבים העצמיים של הערכים העצמיים

מציאת בסיסים למרחבים העצמיים

בדיקה האם המטריצה לכסינה, ואם כן מציאת המטריצה המלכסנת

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים