אנליזת פורייה ויישומים קיץ תשעב/סיכומים/הרצאות/30.7.12
הערה: השיעור החל בחזרה על כמה מהמושגים הבסיסיים באלגברה לינארית: מרחב לינארי, צירוף לינארי, תלות וקטורים, בסיס, מרחבים לינאריים של פונקציות (כגון 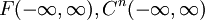 ), מכפלה פנימית (כגון
), מכפלה פנימית (כגון 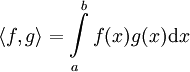 ב־
ב־![C[a,b]](/images/math/d/9/3/d930e3053f32dbc51f14e870df59674d.png) ), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (
), נורמה, אי־שיוויון קושי־שוורץ (Cauchy-Schwarz) (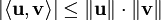 ), מרחבי הסדרות
), מרחבי הסדרות 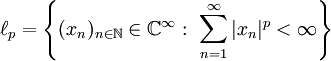 עם
עם 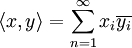 ואורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים הקשים לזכירה והחדשים:
ואורתוגונליות. חזרה זו אינה מופיעה כאן במלואה, אך נפרט את הנושאים הקשים לזכירה והחדשים:
תוכן עניינים
אי־שיוויון הולדר (Holder)
אם 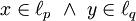 כאשר
כאשר 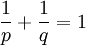 (כלומר,
(כלומר, 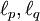 צמודים) אזי
צמודים) אזי 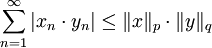 .
.
הוכחה
נעזר באי־שיוויון יונג (Jung): 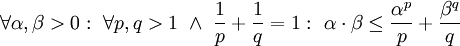 . נבחר עבור
. נבחר עבור  כרצוננו
כרצוננו 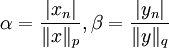 , ונסכום לכל
, ונסכום לכל  :
: 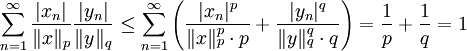 . נכפול ב־
. נכפול ב־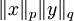 ונקבל את הדרוש.
ונקבל את הדרוש. 
קירוב לווקטור
נניח ש־ מרחב לינארי,
מרחב לינארי, 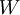 תת־מרחב ו־
תת־מרחב ו־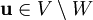 . נרצה להראות שקיים וקטור יחיד
. נרצה להראות שקיים וקטור יחיד 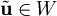 שהוא קירוב ל־
שהוא קירוב ל־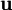 ב־
ב־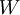 , כלומר שעבורו
, כלומר שעבורו 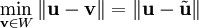 .
.
מובן של מציאת קירוב
הקירוב הטוב ביותר ל־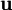 ב־
ב־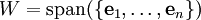 הוא
הוא 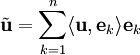 .
.
טענת עזר
יהי  מרחב מכפלה פנימית, ותהי
מרחב מכפלה פנימית, ותהי 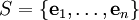 קבוצה אורתונורמלית ב־
קבוצה אורתונורמלית ב־ . אם
. אם 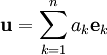 אזי
אזי 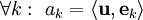 .
.
הוכחה
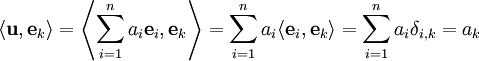

את ההמשך עשינו בשיעור שאחריו:
הוכחה
הגדרה: 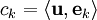 נקרא "מקדם פורייה".
נקרא "מקדם פורייה".
צריך להוכיח ש־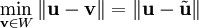 . אזי יהי
. אזי יהי 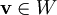 ונסמן
ונסמן 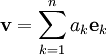 . לכן
. לכן
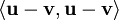
|

|
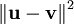
|
||||
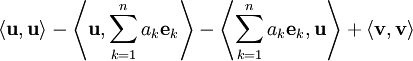
|

|
|||||
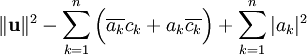
|

|
|||||
מתקיים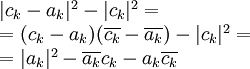
|
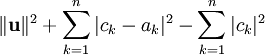
|

|
||||
המקרה המינימלי הוא כאשר 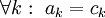
|
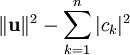
|
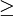
|
מכאן ש־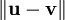 מינימלי כאשר
מינימלי כאשר 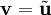 .
.  התוצאה נותנת לנו גם את אי־שיוויון בסל:
התוצאה נותנת לנו גם את אי־שיוויון בסל: 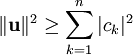 .
.
הכללה
בהינתן בסיס אורתוגונלי 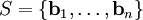 של
של 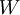 (שאינו בהכרח אורתונורמלי) ניתן להכליל את הנוסחה הנ״ל ל־
(שאינו בהכרח אורתונורמלי) ניתן להכליל את הנוסחה הנ״ל ל־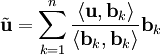 .
.
הוכחה
 בסיס ולכן וקטור האפס אינו נמצא בו. לפיכך הקבוצה
בסיס ולכן וקטור האפס אינו נמצא בו. לפיכך הקבוצה 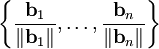 מוגדרת ואורתונורמלית, ולבסוף
מוגדרת ואורתונורמלית, ולבסוף 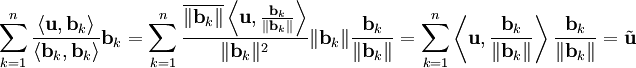

תרגיל
נתבונן בממ״פ של פונקציות רציפות בקטע ![[-1,1]](/images/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) . נגדיר מ״פ באופן הבא:
. נגדיר מ״פ באופן הבא: 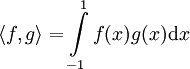 . מצאו קירוב ל־
. מצאו קירוב ל־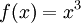 בתת־מרחב הנפרש ע״י המערכת האורתונורמלית
בתת־מרחב הנפרש ע״י המערכת האורתונורמלית 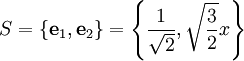 .
.
פתרון
מתקיים: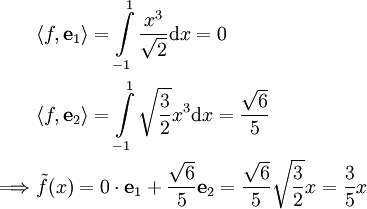
ולפיכך 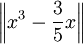 מינימלי בקטע.
מינימלי בקטע. 