לינארית 2 לתיכוניסטים תש"ע

$\begin{bmatrix} \lambda & 0 & 0 \\ 0 &\lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix}$

הוראות

כאן המקום לשאול שאלות. כל שעליכם לעשות הוא ללחוץ על [עריכה] (משמאל לכותרת "שאלות"), להוסיף בתחתית הדף את השורה הבאה:

== כותרת שאלה ==

לכתוב מתחתיה את השאלה שלכם, וללחוץ על 'שמירה'.

(אין צורך להרשם לאתר. רק לעקוב אחרי ההוראות הפשוטות...)

ארכיון

ארכיון 1 - שאלות על תרגילים 1-4

ארכיון 2 - שאלות על תרגילים 5-8

ארכיון 3 - שאלות על תרגילים 10-11

ארכיון 4 - שאלות על תרגיל 12 והמבחן

שאלות

שאלה

איך מוכיחים שכל מטריצה אלכסונית מעל המרוכבים חופפת למטריצה אלכסונית שיש בה רק את הערכים 0,1. מעל הממשיים, המטריצה חופפת למטריצה עם ערכים 0,1,-1.

שאלה

אם x1...xm ע"ע של A. אז מהם הע"ע של A^-1 ושל A^2?

שאלה

יש שאלה שאני לא יודע לפתור: הוכח או הפרך - אם הפולינום האופייני של שתי מטריצות שווה וכן הפולינום המינימלי, אז המטריצות דומות.

שאלה

הי חברים מישהו יכול לעזור לי אם השאלה הבאה: יהיT:V→V ה"ל, כך שלכל : v∈

      T(v),v> =0> הוכח : T=0.

שאלה

איך מוכיחים שאם שתי מטריצות דומות אז לכל עע שלהן יש אותו ריבוי גיאומטרי. חשבנו אולי להשתמש בצורת ג'ורדן אבל לא נתון שהפולינום שלהן מתפרק לגורמים לינארים.

תשובה

דבר ראשון, אפשר לעשות צורת ז'רדן מעל המרוכבים, וברור שלע"ע ממשי יהיו רק ו"ע ממשיים.

דבר שני, צריך לזכור שמטריצה הפיכה היא מטריצת מעבר בין בסיסים. לכן אם תיקח את הו"ע העצמיים של המטריצה, תהפוך את הקואורדינטות שלהם לבסיס המתאים למטריצה ההפיכה (עמודותיה) הכפל בה יהפוך את הקואורדינטות בחזרה לבסיס הסטנדרטי, המטריצה תכפול אותו בע"ע ואז המטריצה ההופכית תחזיר את זה לקואורדינטות החדשות.

עכשיו אם וקטורים הם בת"ל גם הקואורדינטות שלהם לפי בסיס כלשהו בת"ל ולכן תקבל את אותו המימד של המרחב העצמי (כלומר ריבוי גיאומטרי) בעזרת וקטורי הקואורדינטות של הו"ע.

אבל

אני יודע שאם לשתי מטריצות יש אותם ו"ע אז יש להן אותם מרחבים עצמיים? אם כן, איך? תודה.

ועוד שאלה

בהוכחה של המשפט, שלV מ"ו מעל R יש ת"מ אינווריאנטי ממימד 1 או 2 סימנו את הע"ע המרוכב והו"ע המרוכב לפי ממשי + i מדומה ואז קיבלנו ש: שתי משוואות שמקשרות בין המטריצה, החלקים המדומים\ממשיים של הו"ע והע"ע. איך ממשיכים הלאה? איך זה עוזר?

תשובה

מעל המרוכבים קיים ל$A$ וקטור עצמי אחד לפחות עם ע"ע אחד לפחות תמיד. [תרגיל: האם יכול להיות שקיים רק אחד?]

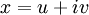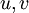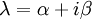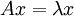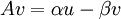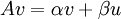נסמן $x=u+iv$ ו"ע כאשר $u,v$ וקטורים ממשיים, ונסמן $\lambda = \alpha + i\beta$ הע"ע המתאים. לכן $Ax=\lambda x$ נפתח את הביטוי, נשווה את הצד הדמיוני והממשי ונקבל 2 משוואות $Av=\alpha u - \beta v$ ו $Av=\alpha v + \beta u$. אז רואים בקלות שלכל וקטור 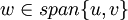$w \in span\{u,v\}$ מתקיים 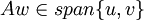$Aw \in span\{u,v\}$ ולכן האופרטור אינווריאנטי תחת התת מרחב $span\{u,v\}$.

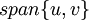תודה! (:

שאלה

למה לכל פונ' ריבועית כללית יש את הצורה q(x)=(x^t)Ax ?

תשובה

ראינו בתרגיל שכל תבנית ריבועית 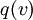$q(v)$ מתאימה לתבנית בי לינארית סימטרית 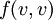$f(v,v)$, ולמדנו שלכל תבנית בי לנארית יש מטריצה $[f]$ כך ש$f(v,u)=v^t[f]u$ ולמדנו שהמטריצה של תבנית בי לינארית היא סמטרית אם"ם התבנית סמטרית.

שאלה

מישהו אמר לי ששאלו את מרצה הקבוצה השנייה האם יהיה פירוק פולרי במבחן והוא אמר שלא...יש מישהו שיכול לאמת את זה כדי שאהיה בטוח?

שאלה

האם ידועה החלוקה בין ציון הבוחן, המבחן ושיעורי הבית? האם יש אפשרות ליידע את כולנו בממוצע הציונים בשיעורי הבית, כולל שיעורי הבית האחרונים? תודה רבה!!

שאלה

כתבנו בהרצאה על שניוניות ש אפשר לסדר את הע"ע של T האופרטור הצל"ע בסדר כזה, כך שהראשונים יהיו שונים מ0, ובסוף יהיו שווים ל0, ושהRANK של T שקול למס' הע"ע השונים. למה זה?

טוב הבנתי לבד חח, זה בגלל שהראנק של אופרטור שקול לראנק של ההצגה שלו לפי בסיס כלשהו ללא תלות בבסיס...

שאלה

בהוכחה של המשפט: A לכסינה \iff הפולינום המינימלי שלה הוא מהצורה m_A(t)=(t-\lambda_1)\cdots(t-\lambda_k) עבור \lambda_1,...,\lambda_k הע"ע השונים של A

בכיוון אחד ההוכחה היא טיפה מסובכת. אי אפשר להוכיח גם את הכיוון הראשון בעזרת בלוקי ז'ורדן? A לכסינה לכן היא דומה למטריצה אלכסונית. אפשר להסתכל על האלכסון כבלוקים בגודל 1X1 וזהו הבלוק הגדול ביותר לכל ע"ע.. ולכן החזקה הגדולה ביותר בפולינום המינימלי היא 1... זה טוב?

בקשה

הקישור למבחנים שבאתר של ד"ר צבאן מאוד נחמד, אבל איפה אפשר למצוא את המבחן שבוריס עשה שנה שעברה?? לי לפחות זה נראה הכי יעיל.. אם מישו יודע(:

שאלה

ארז- כתבת לגבי המבחן-# לגבי משפט אוילר, הוא מחולק לחלק מתמטי וחלק פיסיקלי. את החלק הפיסיקלי לא צריך לדעת למבחן, אבל את החלק המתמטי כן (וכל המשפטונים שמובילים להוכחה כמובן). איזה חלק מתמטי יש למשפט? ההצגה של אופרטור אורתוגונלי בצורת בלוקים?

תשובה

זה הנוסח מהמרצה, תבין את הכוונה שלו מהמחברת. אני מניח שזה אכן הבלוקים, והמשמעות שלהם, שאותה הייתם צריכים להבין כבר בתרגיל 12 ולצערי חלקכם לא הבין אותה.