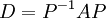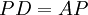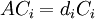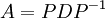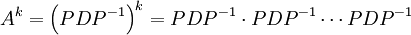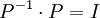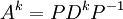לכסון מטריצה

הגדרה: תהי A מטריצה ריבועית.

אומרים כי A מטריצה לכסינה אם היא דומה למטריצה אלכסונית

משפט.

תהי 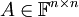$A\in\mathbb{F}^{n\times n}$ מטריצה ריבועית. A לכסינה אם ורק אם קיים בסיס B למרחב 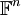$\mathbb{F}^n$ כך שכל הוקטורים בבסיס B הינם וקטורים עצמיים של המטריצה A.

הוכחה.

ראשית, נניח כי המטריצה A לכסינה. לכן קיימת מטריצה אלכסונית D וקיימת מטריצה הפיכה P כך שמתקיים:

$D=P^{-1}AP$

נכפול משמאל במטריצה P לקבל

$PD=AP$

נסמן את עמודות המטריצה P ב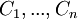$C_1,...,C_n$ ואת איברי האלכסון של D ב$d_1,...,d_n\in\mathbb{F}$.

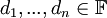לפי שיטת כפל עמודה עמודה אנו שמים לב כי השיוויון

$PD=AP$

שקול לכך שלכל i מתקיים

$AC_i=d_iC_i$

ולכן עמודות P מהוות ו"ע של המטריצה A (כמובן ש 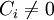$C_i\neq 0$ כיוון שP הפיכה).

בנוסף, כיוון שP הפיכה, עמודותיה מהוות בסיס למרחב 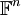$\mathbb{F}^n$.

סה"כ נגיד את B להיות אוסף עמודות P וסיימנו.

בכיוון ההפוך, נניח שיש לנו בסיס כזה B, נשים את איבריו בעמודות מטריצה P. קל לראות כי מתקיים

$PD=AP$

כאשר P הפיכה. לכן נכפול בהופכית לקבל

$D=P^{-1}AP$

כלומר A לכסינה.

דוגמא חשובה לשימוש בלכסינות

באמצעות לכסון ניתן למצוא חזקות גבוהות של מטריצות באופן הבא. נניח A מטריצה לכסינה, לכן קיימת מטריצה אלכסונית D ומטריצה הפיכה P כך שמתקיים:

$A=PDP^{-1}$

ולכן

$A^k=\Big(PDP^{-1}\Big)^k = PDP^{-1}\cdot PDP^{-1} \cdots PDP^{-1}$

אבל

$P^{-1}\cdot P=I$

לכן סה"כ אנחנו מקבלים

$A^k=PD^kP^{-1}$

כאשר להעלות מטריצה אלכסונית בחזקה זה קל מאד.