מדר קיץ תשעב/סיכומים/הרצאות/2.8.12
תוכן עניינים
מד״ר מסדר שני
הצורה הכללית של מד״ר כזו היא 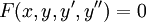 , והפתרון הוא מהצורה
, והפתרון הוא מהצורה 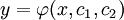 .
.
בעיית קושי מסדר 2
זו בעיה שבה אנו נדרשים לפתור מד״ר עם שני תנאי התחלה 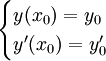 (מובן ש־
(מובן ש־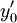 אינו הנגזרת של הקבוע
אינו הנגזרת של הקבוע 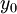 , אלא ערך הנגזרת בנקודה
, אלא ערך הנגזרת בנקודה  ).
).
סוגים נפוצים
סוג 1
מתקיים 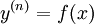 . ניתן לפתור זאת ע״י אינטגרציה
. ניתן לפתור זאת ע״י אינטגרציה  פעמים (במקרה שלנו,
פעמים (במקרה שלנו, 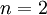 ).
).
סוג 2
אלה מד״ר שבהן ניתן להוריד את סדר המשוואה. עבור מד״ר מסדר 2, נחלק לשני מקרים:
מקרה 1
 לא מופיע במשוואה, כלומר המשוואה מהצורה
לא מופיע במשוואה, כלומר המשוואה מהצורה 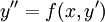 . במקרה זה נציב
. במקרה זה נציב 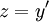 ונקבל מד״ר מסדר ראשון.
ונקבל מד״ר מסדר ראשון.
תרגיל
פתרו את המד״ר 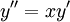 .
.
פתרון
נציב 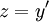 ולכן: ולכן:
|
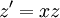
|
|
||||
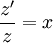
|
|
|||||
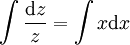
|
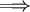
|
|||||
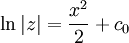
|
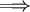
|
|||||
נסמן 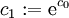 : :
|
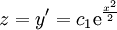
|
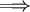
|
||||
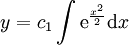
|
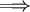
|

מקרה 2
 לא מופיע במשוואה, כלומר המד״ר מהצורה
לא מופיע במשוואה, כלומר המד״ר מהצורה 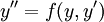 . שוב נגדיר
. שוב נגדיר 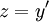 , ואז
, ואז 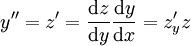 . המד״ר הופכת ל־
. המד״ר הופכת ל־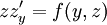 , כלומר מד״ר מסדר ראשון של
, כלומר מד״ר מסדר ראשון של 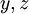 . נובע ש־
. נובע ש־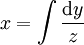 .
.
תרגיל
פתרו 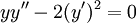 .
.
פתרון
נציב 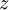 באופן הנ״ל ונקבל
באופן הנ״ל ונקבל
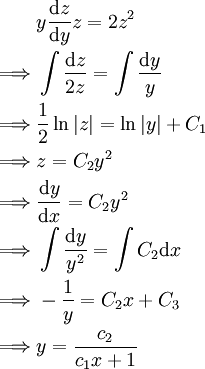

משוואות ריקטי
אלה מד״ר מהצורה 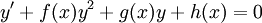 . פתרון כללי של משוואת ריקטי הוא מהצורה
. פתרון כללי של משוואת ריקטי הוא מהצורה 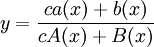 , ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה.
, ולכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה.
הוכחה
ראשית, נוכיח שלכל ביטוי מהצורה הנ״ל קיימת משוואת ריקטי מתאימה: מתקיים 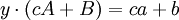 ולכן
ולכן 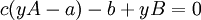 . נגזור את שני האגפים ונקבל
. נגזור את שני האגפים ונקבל 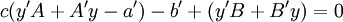 . נציג את שתי המשוואות האחרונות בצורה
. נציג את שתי המשוואות האחרונות בצורה 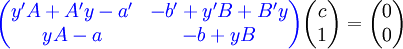 ונשים לב שהמטריצה הכחולה מאפסת וקטור שאינו וקטור האפס, ולפיכך הדטרמיננטה שלה היא 0:
ונשים לב שהמטריצה הכחולה מאפסת וקטור שאינו וקטור האפס, ולפיכך הדטרמיננטה שלה היא 0: 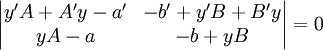 . נחשב את הדטרמיננטה ונגלה ש־
. נחשב את הדטרמיננטה ונגלה ש־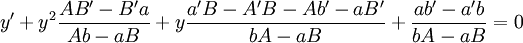 , כדרוש.
, כדרוש.
לצד השני, יהי 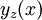 פתרון רגולרי של משוואת ריקטי. נציב במד״ר
פתרון רגולרי של משוואת ריקטי. נציב במד״ר 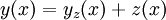 (כאשר
(כאשר 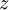 פונקציה לא ידועה) ונגלה ש־
פונקציה לא ידועה) ונגלה ש־
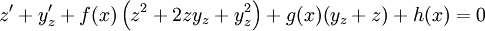
|
||||||
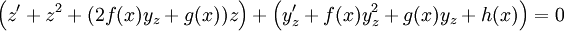
|
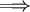
|
|||||
 פתרון, לכן: פתרון, לכן:
|
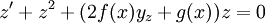
|
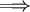
|
לכן 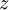 פתרון של משוואת ברנולי עם
פתרון של משוואת ברנולי עם 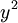 , ולפיכך הוא מהצורה
, ולפיכך הוא מהצורה 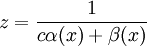 . לבסוף הפתרון מהצורה
. לבסוף הפתרון מהצורה 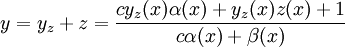 .
. 
מערכת מד״ר מסדר ראשון
זו מערכת מהצורה 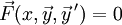 כאשר
כאשר 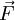 היא מערכת של
היא מערכת של  פונקציות. המערכת היא ב־
פונקציות. המערכת היא ב־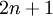 משתנים. בצורה נורמלית:
משתנים. בצורה נורמלית: 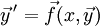 . לפיכך הפתרון הכללי הינו מהצורה
. לפיכך הפתרון הכללי הינו מהצורה 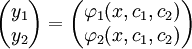 . לדוגמה,
. לדוגמה, 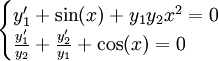 היא מערכת מד״ר.
היא מערכת מד״ר.
בעיית קושי
במערכת מד״ר מסדר 1, בעיית קושי היא לפתור את המד״ר עם תנאי ההתחלה 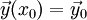 .
.
משפט
מד״ר מסדר  (נורמלית/לינארית/לינארית־הומוגנית) שקולה למערכת של
(נורמלית/לינארית/לינארית־הומוגנית) שקולה למערכת של  מד״ר מסדר ראשון (נורמליות/לינאריות/לינאריות־והומוגניות). אם למד״ר מסדר גבוה נתונים ערכי ההתחלה
מד״ר מסדר ראשון (נורמליות/לינאריות/לינאריות־והומוגניות). אם למד״ר מסדר גבוה נתונים ערכי ההתחלה 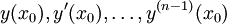 אז המד״ר שקולה לבעיית קושי עבור המערכת.
אז המד״ר שקולה לבעיית קושי עבור המערכת.
הוכחה
נתונה המד״ר 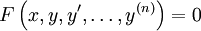 ונסמן
ונסמן 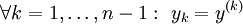 . לכן
. לכן 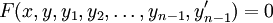 . נוסיף את המד״ר הבאות:
. נוסיף את המד״ר הבאות: 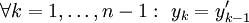 . המערכת שקולה למד״ר המקורית והיא נורמלית/לינארית/לינארית־הומוגנית בהתאם למערכת המקורית.
. המערכת שקולה למד״ר המקורית והיא נורמלית/לינארית/לינארית־הומוגנית בהתאם למערכת המקורית. 
דוגמה
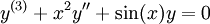 . נציב
. נציב 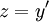 ו־
ו־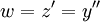 ולפיכך
ולפיכך 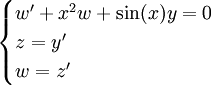 .
.
מד״ר סתומות מסדר 1
אלה מד״ר 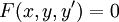 שאנו לא יודעים כיצד להביאן לצורה נורמלית.
שאנו לא יודעים כיצד להביאן לצורה נורמלית.
סוגים נפוצים
מקרה 1
משוואה מסדר 1 וממעלה  :
: 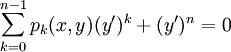 . מכאן שקיימות פונקציות
. מכאן שקיימות פונקציות 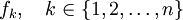 שעבורן
שעבורן 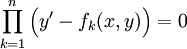 .
.
תרגיל
פתרו 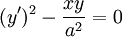 .
.
פתרון
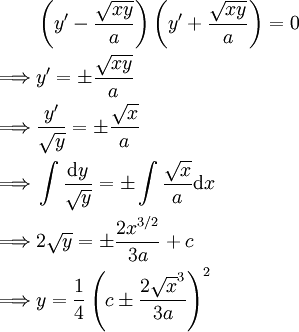

מקרה 2
 לא מופיעה במד״ר. צורתה
לא מופיעה במד״ר. צורתה 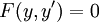 , ובהצבת
, ובהצבת 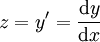 נקבל
נקבל 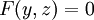 . נשים לב ש־
. נשים לב ש־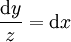 ולכן
ולכן 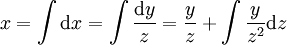 . לפיכך, אם
. לפיכך, אם 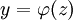 אזי
אזי 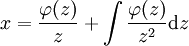 .
.
תרגיל
פתרו 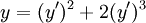 .
.
פתרון
נסמן 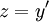 ונציב במד״ר:
ונציב במד״ר: 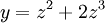 . עתה
. עתה 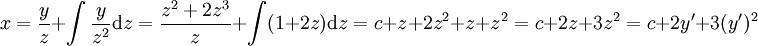 , וזו מד״ר ממקרה 1, שאותו אנו כבר יודעים לפתור.
, וזו מד״ר ממקרה 1, שאותו אנו כבר יודעים לפתור. 
מקרה 3
 לא מופיעה,
לא מופיעה, 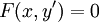 . שוב נציב
. שוב נציב 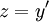 , ונניח
, ונניח 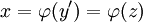 . אזי
. אזי 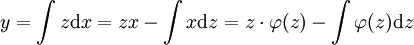 .
.
תרגיל
פתרו 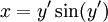 .
.
פתרון
אחרי הצבה 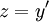 נקבל
נקבל 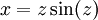 ולבסוף
ולבסוף 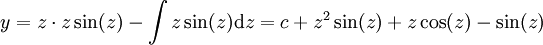 . נציב חזרה
. נציב חזרה 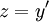 ונקבל את מקרה 2.
ונקבל את מקרה 2. 
מקרה 4
 מופיעה ו־
מופיעה ו־ לא, כלומר
לא, כלומר 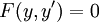 , והמד״ר סתומה. כרגיל, נגדיר
, והמד״ר סתומה. כרגיל, נגדיר 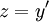 . אם
. אם 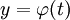 ו־
ו־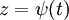 אזי
אזי 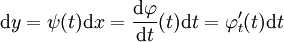 , ומכאן ש־
, ומכאן ש־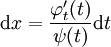 . לבסוף,
. לבסוף, 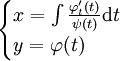 .
.
תרגיל
פתרו 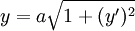 .
.
פתרון
נסמן 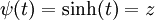 , נציב במד״ר ונקבל
, נציב במד״ר ונקבל 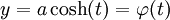 . כמו כן,
. כמו כן, 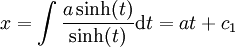 . עתה,
. עתה, 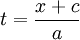 ולכן
ולכן 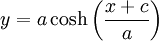 .
. 
מקרה 5
 מופיעה ו־
מופיעה ו־ לא, כלומר
לא, כלומר 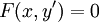 , והמד״ר סתומה. נציב
, והמד״ר סתומה. נציב 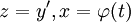 ולכן
ולכן 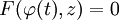 . נסמן
. נסמן 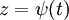 ונגלה כי
ונגלה כי 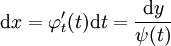 . מאינטגרציה ולפי הגדרת
. מאינטגרציה ולפי הגדרת 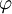 נקבל
נקבל 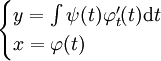 .
.