מדר קיץ תשעב/סיכומים/הרצאות/31.7.12
תוכן עניינים
דוגמה
נניח שגודל החוב ממשכנתה בזמן מסוים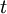 הוא
הוא 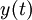 . הריבית היא
. הריבית היא  ליחידת זמן וההחזר הוא
ליחידת זמן וההחזר הוא 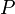 ליחידת זמן. אזי
ליחידת זמן. אזי 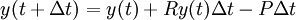 . אם נניח שהבנק מחשב את הריבית באופן רציף נקבל
. אם נניח שהבנק מחשב את הריבית באופן רציף נקבל 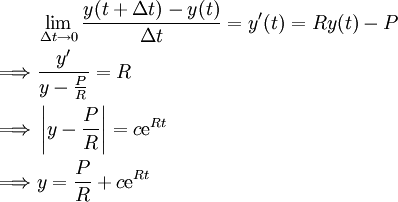
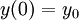 . לכן
. לכן 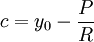 ולבסוף
ולבסוף 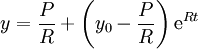 . אנו נסיים לשלם את המשכנתה כאשר
. אנו נסיים לשלם את המשכנתה כאשר 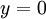 , כלומר כאשר
, כלומר כאשר 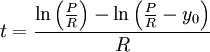 .
. 
מד״ר מסוג 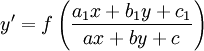
כבר למדנו לפתור מד״ר מהצורה 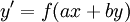 , והיום נלמד גם
, והיום נלמד גם 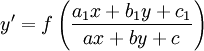 .
.
מקרה 1
נניח ש־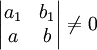 . נסמן
. נסמן 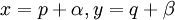 ולכן
ולכן 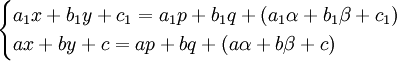 . נדרוש שהמקדמים החופשיים יהיו 0 בשני המקרים ולכן
. נדרוש שהמקדמים החופשיים יהיו 0 בשני המקרים ולכן 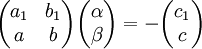 . נקבל
. נקבל 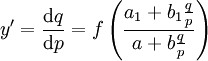 , וזו מד״ר מהצורה
, וזו מד״ר מהצורה 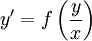 , שאותה אנו יודעים לפתור.
, שאותה אנו יודעים לפתור.
דוגמה
נפתור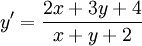 . נציב
. נציב 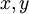 כנ״ל ולפיכך
כנ״ל ולפיכך 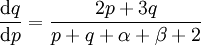 עלינו לדרוש ש־
עלינו לדרוש ש־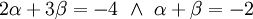 ומכך נובע
ומכך נובע 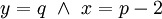 . נסמן
. נסמן 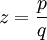 ואז
ואז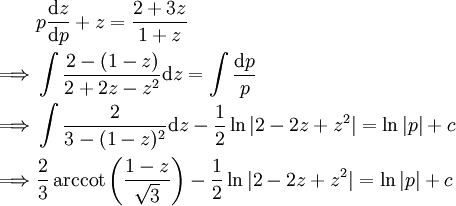
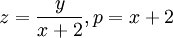 וקיבלנו את הפתרון בצורה של פונקציה סתומה.
וקיבלנו את הפתרון בצורה של פונקציה סתומה.
מקרה 2: נסמן 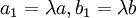 ואז
ואז 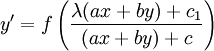 . נציב
. נציב 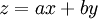 ואנו כבר יודעים לפתור זאת.
ואנו כבר יודעים לפתור זאת.
מד״ר לינארית מסדר I
זו מד״ר מהצורה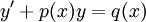 כאשר
כאשר 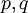 לאו דווקא לינאריות. היא תקרא הומוגנית אם
לאו דווקא לינאריות. היא תקרא הומוגנית אם 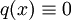 , ובמקרה זה נקבל:
, ובמקרה זה נקבל: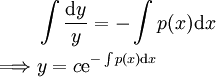
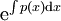 ונשים לב שמקבלים
ונשים לב שמקבלים 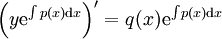 . לכן
. לכן 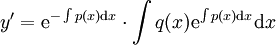 .
.
וריאצית הפרמטרים
נניח שהפתרון הוא 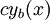 (במקרה ההומוגני) או
(במקרה ההומוגני) או 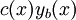 (במקרה הלא הומוגני). נציב זאת במד״ר ונקבל
(במקרה הלא הומוגני). נציב זאת במד״ר ונקבל 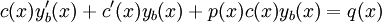 ולכן
ולכן 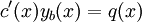 . נותר לפתור את המד״ר
. נותר לפתור את המד״ר 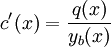
דוגמה
נתונה מד״ר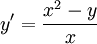 עם תנאי התחלה
עם תנאי התחלה 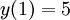 . אזי
. אזי 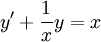 ולכן, מפני שזו מד״ר לינארית מסוג I,
ולכן, מפני שזו מד״ר לינארית מסוג I,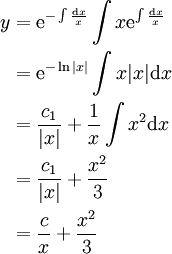
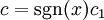 . נציב את תנאי ההתחלה:
. נציב את תנאי ההתחלה: 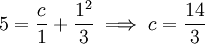 , לכן
, לכן 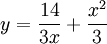 .
.
משוואות ברנולי
אלה מד״ר מהצורה 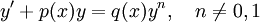 . אם
. אם 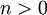 אז
אז 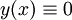 פתרון (רגולרי או סינגולרי). אם
פתרון (רגולרי או סינגולרי). אם 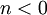 אזי
אזי 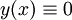 אינו פתרון, לכן נוכל להתייחס למד״ר השקולה
אינו פתרון, לכן נוכל להתייחס למד״ר השקולה 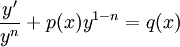 ולהציב
ולהציב 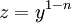 . נקבל
. נקבל 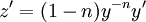 ואז
ואז 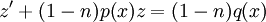 , שהיא מד״ר לינארית מסוג I. לפיכן
, שהיא מד״ר לינארית מסוג I. לפיכן 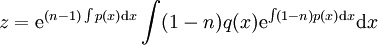 . לבסוף,
. לבסוף, ![y=\sqrt[1-n]{\mathrm e^{(n-1)\int p(x)\mathrm dx}\int(1-n)p(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx}](/images/math/9/5/8/9583d2b467d4aed1134b74cb7d97cc6c.png) .
.
עבור 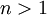 ,
, 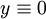 פתרון פרטי (רגולרי), עבור
פתרון פרטי (רגולרי), עבור 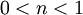 זה פתרון סינגולרי, ועבור
זה פתרון סינגולרי, ועבור 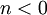 הוא אינו פתרון.
הוא אינו פתרון.
דוגמה
נפתור 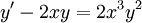 . עבור הסימנים הנ״ל
. עבור הסימנים הנ״ל 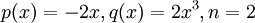 ואז
ואז 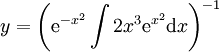 . נציב
. נציב 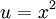 ואז
ואז 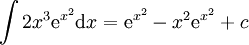 , ולבסוף
, ולבסוף 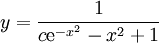 .
.
מד״ר מדויקת
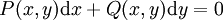 . נניח שקיימת
. נניח שקיימת 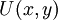 עבורה
עבורה 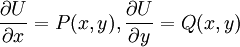 . לפיכך
. לפיכך 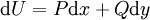 והמד״ר הופכת ל־
והמד״ר הופכת ל־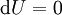 כלומר
כלומר 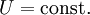 . אם היא קיימת אזי
. אם היא קיימת אזי 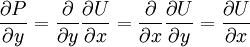 .
.
דוגמה
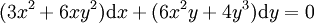 . לפיכך
. לפיכך 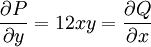 , כדרוש. מתקיים
, כדרוש. מתקיים 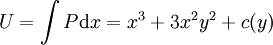 . נדרוש ש־
. נדרוש ש־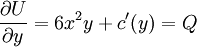 ואז
ואז 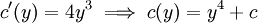 . לבסוף נדרוש ש־
. לבסוף נדרוש ש־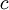 יקיים
יקיים 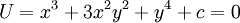 (נשים לב שניתן לבחור גם כל קבוע אחר מלבד 0, אבל שינוי בסה״כ יחליף את הקבוע
(נשים לב שניתן לבחור גם כל קבוע אחר מלבד 0, אבל שינוי בסה״כ יחליף את הקבוע 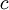 ).
).
גורם אינטגרציה
אם נכפיל את אגפי המד״ר ב־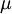 נקבל
נקבל 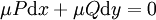 . לפיכך
. לפיכך 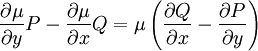 .
.
מקרה 1
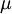 תלוי רק ב־
תלוי רק ב־ . לכן
. לכן 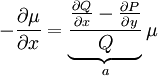 לפיכך
לפיכך 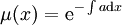 . נשים לב ש־
. נשים לב ש־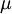 תלוי רק ב־
תלוי רק ב־ אם״ם
אם״ם  תלוי רק ב־
תלוי רק ב־ .
.
מקרה 2
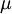 תלוי רק ב־
תלוי רק ב־ . זה מתקיים אם״ם
. זה מתקיים אם״ם 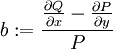 תלוי רק ב־
תלוי רק ב־ , ואז
, ואז 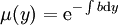 .
.
דוגמה
נפתור את המד״ר 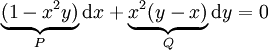 . אזי
. אזי 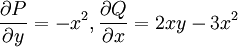 . נשים לב ש־
. נשים לב ש־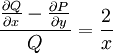 , כלומר תלוי אך ורק ב־
, כלומר תלוי אך ורק ב־ , ולכן נגדיר
, ולכן נגדיר 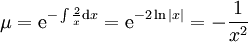 . נכפיל את אגפי המד״ר ב־
. נכפיל את אגפי המד״ר ב־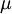 ונקבל
ונקבל 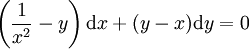 . המד״ר החדשה מקיימת
. המד״ר החדשה מקיימת 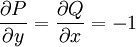 , ומכאן נוכל להמשיך לפתור כרגיל.
, ומכאן נוכל להמשיך לפתור כרגיל. 
הערה: נשים לב ש־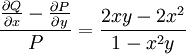 תלוי גם ב־
תלוי גם ב־ וגם ב־
וגם ב־ , ולכן הגדרת
, ולכן הגדרת 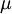 התלויה ב־
התלויה ב־ לא תועיל לנו.
לא תועיל לנו.