הבדלים בין גרסאות בדף "מדר קיץ תשעב/סיכומים/הרצאות/31.7.12"
(יצירת דף עם התוכן "== דוגמה == נניח שגודל החוב ממשכנתה בזמן מסוים <math>t</math> הוא <math>y(t)</math>. הריבית היא <math>R</math> ליח...") |
|||
| שורה 1: | שורה 1: | ||
| − | == דוגמה == | + | = מד״ר מסדר ראשון {{הערה|(המשך)}} = |
| − | נניח שגודל החוב ממשכנתה בזמן מסוים <math>t</math> הוא <math>y(t)</math>. הריבית היא <math>R</math> ליחידת זמן וההחזר הוא <math>P</math> ליחידת זמן. אזי <math>y(t+\Delta t)=y(t)+Ry(t)\Delta t-P\Delta t</math>. אם נניח שהבנק מחשב את הריבית באופן רציף נקבל {{left|<math>\begin{align}&\lim_{\Delta t\to0}\frac{y(t+\Delta t)-y(t)}{\Delta t} | + | == דוגמה שימושית == |
| + | נניח שגודל החוב ממשכנתה בזמן מסוים <math>t</math> הוא <math>y(t)</math>. הריבית היא <math>R</math> כחלק מגודל החוב ליחידת זמן, וההחזר הוא <math>P</math> בכמות כסף ליחידת זמן. אזי <math>y(t+\Delta t)=y(t)+Ry(t)\Delta t-P\Delta t</math>. אם נניח שהבנק מחשב את הריבית באופן רציף וש־<math>y\not\equiv\frac PR</math> נקבל {{left|<math>\begin{align}&y'(t)=\lim_{\Delta t\to0}\frac{y(t+\Delta t)-y(t)}{\Delta t}=Ry(t)-P\\\implies&\frac{y'}{y-\frac PR}=R\\\implies&\int\frac{\mathrm dy}{y-\frac PR}=\int R\mathrm dt\\\implies&\left|y-\frac PR\right|=c_1\mathrm e^{Rt}\\\implies&y=\frac PR+c\mathrm e^{Rt}\end{align}</math>}} | ||
| + | נוסיף תנאי התחלה <math>y(0)=y_0</math>. לכן <math>c=y_0-\frac PR</math> ולבסוף <math>y=\frac PR+\left(y_0-\frac PR\right)\mathrm e^{Rt}</math>. ניתן לראות שאם <math>y_0>\frac PR</math> אזי הפונקציה עולה, כלומר החוב גדל בהתמדה ולעולם לא נחזיר את ההלוואה. לעומת זאת, אם <math>y\equiv\frac PR=y_0</math> אז החוב נותר קבוע כל הזמן, ואם <math>y_0<\frac PR</math> אזי נסיים לשלם את המשכנתה כאשר <math>y=0</math>, כלומר כאשר <math>t=\frac{\ln\left(\frac PR\right)-\ln\left(\frac PR-y_0\right)}R</math>. {{משל}} | ||
| − | == מד״ר | + | == מד״ר פתירות ע״י משוואה הומוגנית == |
| − | כבר למדנו לפתור מד״ר מהצורה <math>y'=f(ax+by)</math> | + | כבר למדנו לפתור מד״ר מהצורה <math>y'=f(ax+by)</math>. היום נלמד לפתור את <math>y'=f\left(\frac{a_1x+b_1y+c_1}{ax+by+c}\right)</math>. |
=== מקרה 1 === | === מקרה 1 === | ||
| − | נניח ש־<math>\begin{vmatrix}a_1&b_1\\a&b\end{vmatrix}\ne0</math>. נסמן <math>x=p+\alpha | + | נניח ש־<math>\begin{vmatrix}a_1&b_1\\a&b\end{vmatrix}\ne0</math>. נסמן <math>\begin{cases}x=p+\alpha\\y=q+\beta\end{cases}</math> ולכן <math>\begin{cases}a_1x+b_1y+c_1=a_1p+b_1q+{\color{Blue}(a_1\alpha+b_1\beta+c_1)}\\ax+by+c=ap+bq+{\color{Blue}(a\alpha+b\beta+c)}\end{cases}</math>. נדרוש שהמקדמים החופשיים (בכחול) יהיו 0 בשני המקרים, כלומר <math>\begin{pmatrix}a_1&b_1\\a&b\end{pmatrix}\begin{pmatrix}\alpha\\\beta\end{pmatrix}=-\begin{pmatrix}c_1\\c\end{pmatrix}</math>. נקבל <math>\frac{\mathrm dq}{\mathrm dp}=\frac{\mathrm dy}{\mathrm dx}=y'=f\left(\frac{a_1+b_1\frac qp}{a+b\frac qp}\right)</math>, וזו מד״ר מהצורה <math>q'=f\left(\frac qp\right)</math>, שאותה אנו יודעים לפתור. |
==== דוגמה ==== | ==== דוגמה ==== | ||
| − | נפתור <math>y'=\frac{2x+3y+4}{x+y+2}</math>. נציב <math>x,y</math> כנ״ל ולפיכך <math>\frac{\mathrm dq}{\mathrm dp}=\frac{2p+3q}{p+q+\alpha+\beta+2}</math> עלינו לדרוש ש־<math>2\alpha+3\beta=-4\ \and\ \alpha+\beta=-2</math> | + | נפתור <math>y'=\frac{2x+3y+4}{x+y+2}</math>. נציב <math>x,y</math> כנ״ל ולפיכך <math>\frac{\mathrm dq}{\mathrm dp}=\frac{2p+3q+2\alpha+3\beta+4}{p+q+\alpha+\beta+2}</math>. עלינו לדרוש ש־<math>2\alpha+3\beta=-4\ \and\ \alpha+\beta=-2</math> ומכאן ש־<math>\frac{\mathrm dq}{\mathrm dp}=\frac{2p+3q}{p+q}=\frac{2+3\frac qp}{1+\frac qp}</math> וגם <math>y=q\ \and\ x=p-2</math>. נסמן <math>z=\frac pq</math> ואז{{left|<math>\begin{align}&\frac{2+3z}{1+z}=\frac{\mathrm dq}{\mathrm dp}=\frac{\mathrm d(pz)}{\mathrm dp}=p\frac{\mathrm dz}{\mathrm dp}+z\\\implies&\frac{2+2z-z^2}{1+z}=p\frac{\mathrm dz}{\mathrm dp}\\\implies&\frac{1+z}{2+2z-z^2}\mathrm dz=\frac{\mathrm dp}p\\\implies&\int\frac{2-(1-z)}{2+2z-z^2}\mathrm dz=\int\frac{\mathrm dp}p\\\implies&\int\frac2{3-(1-z)^2}\mathrm dz-\frac12\ln|2+2z-z^2|=\ln|p|+c\\\implies&\frac2\sqrt3\mbox{arctanh}\left(\frac{1-z}\sqrt3\right)-\frac12\ln|2+2z-z^2|=\ln|p|+c\end{align}</math>}} |
| + | עתה מציבים <math>z=\frac y{x+2}, p=x+2</math> ומקבלים את הפתרון בצורה של פונקציה סתומה. {{משל}} | ||
| − | מקרה 2 | + | === מקרה 2 === |
| + | אם <math>\begin{vmatrix}a_1&b_1\\a&b\end{vmatrix}=0</math> אז יש <math>\lambda</math> שעבורה <math>a_1=\lambda a\ \and\ b_1=\lambda b</math> ואז <math>y'=f\left(\frac{\lambda(ax+by)+c_1}{(ax+by)+c}\right)</math>. נציב <math>z=ax+by</math> ונפתור כפי שאנו כבר יודעים. | ||
| − | == מד״ר לינארית | + | == מד״ר לינארית מסוג I == |
| − | + | אלה מד״ר מהצורה <math>y'+p(x)y=q(x)</math> כאשר <math>p,q</math> לאו דווקא לינאריות. היא תקרא לינארית־הומוגנית אם <math>q(x)\equiv0</math>, ובמקרה זה נקבל:{{left|<math>\begin{align}&\int\frac{\mathrm dy}y=-\int p(x)\mathrm dx\\\implies&y=c\mathrm e^{-\int p(x)\mathrm dx}\end{align}</math>}} | |
| + | במקרה הלא הומוגני נוכל להכפיל את אגפי המשוואה ב־<math>\mathrm e^{\int p(x)\mathrm dx+c_1}</math> ונקבל <math>y'\mathrm e^{\int p(x)\mathrm dx+c_1}+p(x)y\mathrm e^{\int p(x)\mathrm dx+c_1}=\left(y\mathrm e^{\int p(x)\mathrm dx+c_1}\right)'=q(x)\mathrm e^{\int p(x)\mathrm dx+c_1}</math>. לכן {{left|<math>\begin{align}y&=\mathrm e^{-\int p(x)\mathrm dx-c_1}\left(c_2+\int q(x)\mathrm e^{\int p(x)\mathrm dx+c_1}\mathrm dx\right)\\&=\mathrm e^{-\int p(x)\mathrm dx}\left(c_2\mathrm e^{-c_1}+\mathrm e^{-c_1}\mathrm e^{c_1}\int q(x)\mathrm e^{\int p(x)\mathrm dx}\mathrm dx\right)\\&=\mathrm e^{-\int p(x)\mathrm dx}\left(c+\int q(x)\mathrm e^{\int p(x)\mathrm dx}\mathrm dx\right)\end{align}</math>}} | ||
| − | + | ''הערה:'' מד״ר לינארית־הומוגנית אינה בהכרח מד״ר הומוגנית, כלומר לא בהכרח מתקיים <math>y'=f\left(\frac yx\right)</math> עבור <math>f</math> כלשהי. | |
| − | + | ||
| − | ==== | + | == וריאצית הפרמטרים == |
| − | נתונה | + | נניח שהפתרון הוא <math>cy_b(x)</math> (במקרה ההומוגני) או <math>c(x)y_b(x)</math> (במקרה הלא הומוגני). נציב זאת במד״ר ונקבל <math>c(x)y_b'(x)+c'(x)y_b(x)+p(x)c(x)y_b(x)=q(x)</math>. לכן <math>c'(x)y_b(x),q(x)</math> המקדמים הייחידים שאינם מוכפלים ב־<math>y</math> או ב־<math>y'</math>, ומכאן ש־<math>c'(x)y_b(x)=q(x)</math>. נותר לפתור את המד״ר <math>c'(x)=\frac{q(x)}{y_b(x)}</math>. |
| + | |||
| + | === דוגמה === | ||
| + | נתונה המד״ר <math>y'=\frac{x^2-y}x</math> עם תנאי התחלה <math>y(1)=5</math>. אזי <math>y'+\frac1xy=x</math> ולכן, מפני שזו מד״ר לינארית מסוג I, | ||
| + | {| | ||
| + | {{=|l=y |r=\mathrm e^{-\int\frac{\mathrm dx}x}\left(c+\int x\mathrm e^{\int\frac{\mathrm dx}x}\mathrm dx\right) |c=<math>c\in\mathbb R</math> }} | ||
| + | {{=|r=\mathrm e^{-\ln\vert x\vert}\left(c+\int x\vert x\vert\mathrm dx\right) }} | ||
| + | {{=|r=\frac c{\vert x\vert}+\frac1{\vert x\vert}\int x\vert x\vert\mathrm dx }} | ||
| + | {{=|r=\frac c{\vert x\vert}+\frac{\sgn(x)}{\vert x\vert}\int x^2\mathrm dx |c=<math>\sgn(x)</math> קבוע בכל אחד מהקטעים <math>(-\infty,0),(0,\infty)</math>. לכן נחשב שני מקרים – כאשר <math>x</math> בקטע הראשון וכאשר בקטע השני – ונוציא בכל מקרה את <math>\sgn(x)</math> מחוץ לאינטגרל. התוצאה היא תמיד: }} | ||
| + | {{=|r=\frac c{\vert x\vert}+\frac1x\frac{x^3}3 }} | ||
| + | {{=|r=\frac c{\vert x\vert}+\frac{x^2}3 }} | ||
| + | |} | ||
| + | נציב את תנאי ההתחלה: <math>5=\frac c1+\frac{1^2}3\implies c=\frac{14}3</math>, לכן <math>y=\frac{14}{3|x|}+\frac{x^2}3</math>. {{משל}} | ||
== משוואות ברנולי == | == משוואות ברנולי == | ||
| − | אלה מד״ר מהצורה <math>y'+p(x)y=q(x)y^n,\quad n\ne0,1</math>. אם <math>n>0</math> אז <math>y(x)\equiv0</math> פתרון (רגולרי או סינגולרי). אם <math>n<0</math> אזי <math>y(x)\equiv0</math> אינו פתרון, לכן נוכל להתייחס למד״ר השקולה <math>\frac{y'}{y^n}+p(x)y^{1-n}=q(x)</math> ולהציב <math>z=y^{1-n}</math>. נקבל <math>z'=(1-n)y^{-n}y'</math> ואז <math>z'+(1-n)p(x)z=(1-n)q(x)</math>, שהיא מד״ר לינארית מסוג I. לפיכן <math>z=\mathrm e^{(n-1)\int p(x)\mathrm dx}\int(1-n)q(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx</math> | + | אלה מד״ר מהצורה <math>y'+p(x)y=q(x)y^n,\quad n\ne0,1</math>. אם <math>n>0</math> אז <math>y(x)\equiv0</math> פתרון (רגולרי או סינגולרי). אם <math>n<0</math> אזי <math>y(x)\equiv0</math> אינו פתרון, לכן נוכל להתייחס למד״ר השקולה <math>\frac{y'}{y^n}+p(x)y^{1-n}=q(x)</math> ולהציב <math>z=y^{1-n}</math>. נקבל <math>z'=(1-n)y^{-n}y'</math> ואז <math>z'+(1-n)p(x)z=(1-n)q(x)</math>, שהיא מד״ר לינארית מסוג I. לפיכן <math>z=\mathrm e^{(n-1)\int p(x)\mathrm dx}\left(c+\int(1-n)q(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx\right)</math> ולבסוף, <math>y=\sqrt[1-n]{\mathrm e^{(n-1)\int p(x)\mathrm dx}\left(c+\int(1-n)p(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx\right)}</math>. |
עבור <math>n>1</math>, ‏ <math>y\equiv0</math> פתרון פרטי (רגולרי), עבור <math>0<n<1</math> זה פתרון סינגולרי, ועבור <math>n<0</math> הוא אינו פתרון. | עבור <math>n>1</math>, ‏ <math>y\equiv0</math> פתרון פרטי (רגולרי), עבור <math>0<n<1</math> זה פתרון סינגולרי, ועבור <math>n<0</math> הוא אינו פתרון. | ||
| − | === | + | === תרגיל === |
| − | + | פתרו <math>y'-2xy=2x^3y^2</math>. | |
| + | |||
| + | ==== פתרון ==== | ||
| + | עבור הסימנים הנ״ל <math>p(x)=-2x,q(x)=2x^3,n=2</math> , כלומר <math>y=\sqrt[-1]{\mathrm e^{-x^2}\left(c+\int2x^3\mathrm e^{x^2}\mathrm dx\right)}</math>. נציב <math>u=x^2</math> ואז <math>\int2x^3\mathrm e^{x^2}\mathrm dx=\mathrm e^{x^2}-x^2\mathrm e^{x^2}</math>, ולבסוף <math>y=\frac1{c\mathrm e^{-x^2}-x^2+1}</math>. {{משל}} | ||
== מד״ר מדויקת == | == מד״ר מדויקת == | ||
| − | <math>P(x,y)\mathrm dx+Q(x,y)\mathrm dy=0</math> | + | מד״ר מהצורה <math>P(x,y)\mathrm dx+Q(x,y)\mathrm dy=0</math> כך שקיימת <math>U(x,y)</math> עבורה <math>\frac{\partial U}{\partial x}=P,\frac{\partial U}{\partial y}=Q</math>. לפיכך <math>\mathrm dU=P\mathrm dx+Q\mathrm dy</math> והמד״ר הופכת ל־<math>\mathrm dU=0</math> כלומר <math>U=\text{const.}</math>. תנאי הכרחי ומספיק לקיום <math>U</math> כנ״ל הוא <math>\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}</math> (הכרחי כי <math>\frac{\partial P}{\partial y}=\frac\partial{\partial y}\frac{\partial U}{\partial x}=\frac\partial{\partial x}\frac{\partial U}{\partial y}=\frac{\partial Q}{\partial x}</math>). |
| − | === | + | === תרגיל === |
| − | <math>(3x^2+6xy^2 | + | פתרו <math>\underbrace{\left(3x^2+6xy^2\right)}_P\mathrm dx+\underbrace{\left(6x^2y+4y^3\right)}_Q\mathrm dy=0</math>. |
| − | === | + | ==== פתרון ==== |
| − | + | מתקיים <math>\frac{\partial P}{\partial y}=12xy=\frac{\partial Q}{\partial x}</math>, כדרוש לקיום <math>U</math>. ננסה לחשב <math>U</math> כנ"ל: <math>U=\int P\mathrm dx=x^3+3x^2y^2+c_y(y)</math>. עתה נדרוש ש־<math>\frac{\partial U}{\partial y}=6x^2y+c_y'(y)=Q</math> ואז <math>c'_y(y)=4y^3\implies c_y(y)=y^4+c</math>. לסיכום, פתרון המד״ר הוא <math>U=x^3+3x^2y^2+y^4+c=0</math> (נשים לב שניתן לבחור גם כל קבוע אחר מלבד 0, אבל שינוי כזה בסה״כ יחליף את הקבוע <math>c</math>). {{משל}} | |
| + | |||
| + | == מד״ר לא מדויקת == | ||
| + | תהי <math>P(x,y)\mathrm dx+Q(x,y)\mathrm dy=0</math> מד״ר שאינה מדויקת, ונרצה לפתור אותה ע״י ''גורמי אינטגרציה'': ננסה להכפיל את אגפי המד״ר ב־<math>\mu(x,y)</math> ולקבל מד״ר מדויקת <math>\mu P\mathrm dx+\mu Q\mathrm dy=0</math>. לשם כך <math>\mu</math> צריכה לקיים <math>\frac{\partial(\mu P)}{\partial y}=\frac{\partial(\mu Q)}{\partial x}</math>, ובאופן שקול <math>\frac{\partial\mu}{\partial y}P-\frac{\partial\mu}{\partial x}Q=\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\mu</math> (נשים לב שזו מד״ח). | ||
| + | |||
| + | === מקרה 1 === | ||
| + | <math>\mu</math> תלויה רק ב־<math>x</math>. לכן <math>\frac{\partial\mu}{\partial y}</math> מתאפס ומכאן נובע (כאשר <math>a:=\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}Q</math>) ש־ | ||
| + | {{left|<math>\begin{align}&-\frac{\partial\mu}{\partial x}=a\mu\\\implies&\frac{\partial\mu}\mu\mathrm dx=-a\mathrm dx\\\implies&\mu(x)=\mathrm e^{-\int a\mathrm dx}\end{align}</math>}} | ||
| + | נשים לב ש־<math>\mu</math> תלויה רק ב־<math>x</math> אם״ם <math>a</math> תלויה רק ב־<math>x</math>. | ||
| − | + | === מקרה 2 === | |
| − | <math>\mu</math> | + | <math>\mu</math> תלויה רק ב־<math>y</math>. זה מתקיים אם״ם <math>b:=\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}P</math> תלויה רק ב־<math>y</math>, ואז <math>\mu(y)=\mathrm e^{-\int b\mathrm dy}</math>. |
| − | ==== | + | ==== תרגיל ==== |
| − | <math>\ | + | פתרו את המד״ר <math>\underbrace{\left(1-x^2y\right)}_P\mathrm dx+\underbrace{x^2(y-x)}_Q\mathrm dy=0</math>. |
| − | ===== | + | ===== פתרון ===== |
| − | + | מתקיים <math>\frac{\partial P}{\partial y}=-x^2\ne\frac{\partial Q}{\partial x}=2xy-3x^2</math>, כלומר המד״ר אינה מדויקת. נשים לב ש־<math>\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}Q=\frac2x</math>, כלומר תלויה אך ורק ב־<math>x</math>, ולכן נגדיר <math>\mu=\mathrm e^{-\int\frac2x\mathrm dx}=\mathrm e^{-2\ln|x|}=-\frac1{x^2}</math>. נכפיל את אגפי המד״ר ב־<math>-\mu</math> ונקבל <math>\left(\frac1{x^2}-y\right)\mathrm dx+(y-x)\mathrm dy=0</math>. המד״ר החדשה מקיימת <math>\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}=-1</math>, ומכאן נוכל להמשיך לפתור כרגיל. {{משל}} | |
| − | ''הערה:'' נשים לב ש־<math>\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}P=\frac{2xy-2x^2}{1-x^2y}</math> | + | ''הערה:'' נשים לב ש־<math>\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}P=\frac{2xy-2x^2}{1-x^2y}</math> תלויה גם ב־<math>x</math> וגם ב־<math>y</math>, ולכן הגדרת <math>\mu</math> התלויה ב־<math>y</math> לא תועיל לנו. |
גרסה מ־17:09, 4 באוגוסט 2012
תוכן עניינים
מד״ר מסדר ראשון (המשך)
דוגמה שימושית
נניח שגודל החוב ממשכנתה בזמן מסוים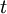 הוא
הוא 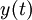 . הריבית היא
. הריבית היא  כחלק מגודל החוב ליחידת זמן, וההחזר הוא
כחלק מגודל החוב ליחידת זמן, וההחזר הוא 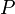 בכמות כסף ליחידת זמן. אזי
בכמות כסף ליחידת זמן. אזי 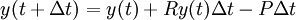 . אם נניח שהבנק מחשב את הריבית באופן רציף וש־
. אם נניח שהבנק מחשב את הריבית באופן רציף וש־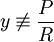 נקבל
נקבל 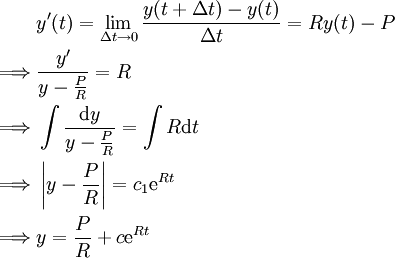
נוסיף תנאי התחלה 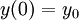 . לכן
. לכן 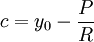 ולבסוף
ולבסוף 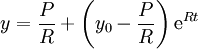 . ניתן לראות שאם
. ניתן לראות שאם 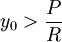 אזי הפונקציה עולה, כלומר החוב גדל בהתמדה ולעולם לא נחזיר את ההלוואה. לעומת זאת, אם
אזי הפונקציה עולה, כלומר החוב גדל בהתמדה ולעולם לא נחזיר את ההלוואה. לעומת זאת, אם 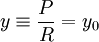 אז החוב נותר קבוע כל הזמן, ואם
אז החוב נותר קבוע כל הזמן, ואם 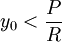 אזי נסיים לשלם את המשכנתה כאשר
אזי נסיים לשלם את המשכנתה כאשר 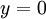 , כלומר כאשר
, כלומר כאשר 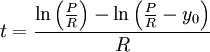 .
. 
מד״ר פתירות ע״י משוואה הומוגנית
כבר למדנו לפתור מד״ר מהצורה 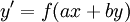 . היום נלמד לפתור את
. היום נלמד לפתור את 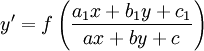 .
.
מקרה 1
נניח ש־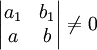 . נסמן
. נסמן 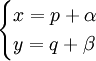 ולכן
ולכן 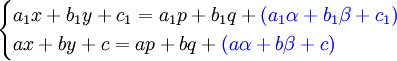 . נדרוש שהמקדמים החופשיים (בכחול) יהיו 0 בשני המקרים, כלומר
. נדרוש שהמקדמים החופשיים (בכחול) יהיו 0 בשני המקרים, כלומר 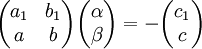 . נקבל
. נקבל 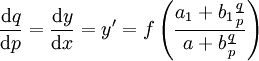 , וזו מד״ר מהצורה
, וזו מד״ר מהצורה 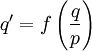 , שאותה אנו יודעים לפתור.
, שאותה אנו יודעים לפתור.
דוגמה
נפתור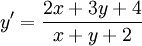 . נציב
. נציב 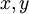 כנ״ל ולפיכך
כנ״ל ולפיכך 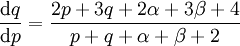 . עלינו לדרוש ש־
. עלינו לדרוש ש־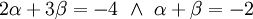 ומכאן ש־
ומכאן ש־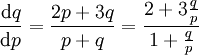 וגם
וגם 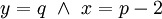 . נסמן
. נסמן 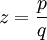 ואז
ואז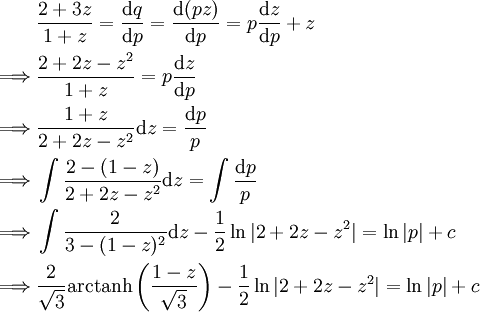
עתה מציבים 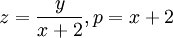 ומקבלים את הפתרון בצורה של פונקציה סתומה.
ומקבלים את הפתרון בצורה של פונקציה סתומה. 
מקרה 2
אם 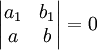 אז יש
אז יש  שעבורה
שעבורה 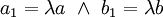 ואז
ואז 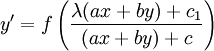 . נציב
. נציב 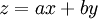 ונפתור כפי שאנו כבר יודעים.
ונפתור כפי שאנו כבר יודעים.
מד״ר לינארית מסוג I
אלה מד״ר מהצורה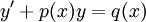 כאשר
כאשר 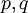 לאו דווקא לינאריות. היא תקרא לינארית־הומוגנית אם
לאו דווקא לינאריות. היא תקרא לינארית־הומוגנית אם 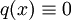 , ובמקרה זה נקבל:
, ובמקרה זה נקבל: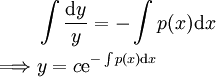
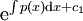 ונקבל
ונקבל 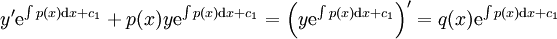 . לכן
. לכן 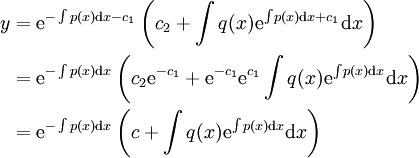
הערה: מד״ר לינארית־הומוגנית אינה בהכרח מד״ר הומוגנית, כלומר לא בהכרח מתקיים 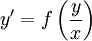 עבור
עבור  כלשהי.
כלשהי.
וריאצית הפרמטרים
נניח שהפתרון הוא 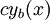 (במקרה ההומוגני) או
(במקרה ההומוגני) או 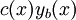 (במקרה הלא הומוגני). נציב זאת במד״ר ונקבל
(במקרה הלא הומוגני). נציב זאת במד״ר ונקבל 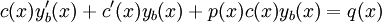 . לכן
. לכן 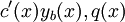 המקדמים הייחידים שאינם מוכפלים ב־
המקדמים הייחידים שאינם מוכפלים ב־ או ב־
או ב־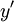 , ומכאן ש־
, ומכאן ש־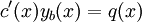 . נותר לפתור את המד״ר
. נותר לפתור את המד״ר 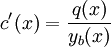 .
.
דוגמה
נתונה המד״ר 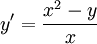 עם תנאי התחלה
עם תנאי התחלה 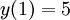 . אזי
. אזי 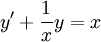 ולכן, מפני שזו מד״ר לינארית מסוג I,
ולכן, מפני שזו מד״ר לינארית מסוג I,
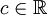
|
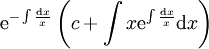
|

|

|
|||
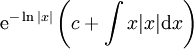
|

|
|||||
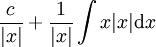
|

|
|||||
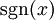 קבוע בכל אחד מהקטעים קבוע בכל אחד מהקטעים 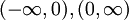 . לכן נחשב שני מקרים – כאשר . לכן נחשב שני מקרים – כאשר  בקטע הראשון וכאשר בקטע השני – ונוציא בכל מקרה את בקטע הראשון וכאשר בקטע השני – ונוציא בכל מקרה את 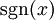 מחוץ לאינטגרל. התוצאה היא תמיד: מחוץ לאינטגרל. התוצאה היא תמיד:
|
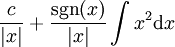
|

|
||||
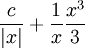
|

|
|||||
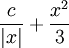
|

|
נציב את תנאי ההתחלה: 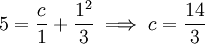 , לכן
, לכן 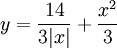 .
. 
משוואות ברנולי
אלה מד״ר מהצורה 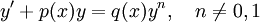 . אם
. אם 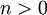 אז
אז 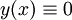 פתרון (רגולרי או סינגולרי). אם
פתרון (רגולרי או סינגולרי). אם 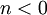 אזי
אזי 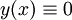 אינו פתרון, לכן נוכל להתייחס למד״ר השקולה
אינו פתרון, לכן נוכל להתייחס למד״ר השקולה 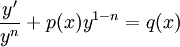 ולהציב
ולהציב 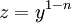 . נקבל
. נקבל 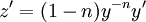 ואז
ואז 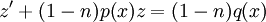 , שהיא מד״ר לינארית מסוג I. לפיכן
, שהיא מד״ר לינארית מסוג I. לפיכן 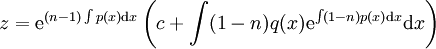 ולבסוף,
ולבסוף, ![y=\sqrt[1-n]{\mathrm e^{(n-1)\int p(x)\mathrm dx}\left(c+\int(1-n)p(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx\right)}](/images/math/f/c/b/fcb3a028ab43a0f694c873d5be157141.png) .
.
עבור 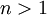 ,
, 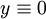 פתרון פרטי (רגולרי), עבור
פתרון פרטי (רגולרי), עבור 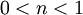 זה פתרון סינגולרי, ועבור
זה פתרון סינגולרי, ועבור 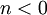 הוא אינו פתרון.
הוא אינו פתרון.
תרגיל
פתרו 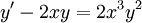 .
.
פתרון
עבור הסימנים הנ״ל 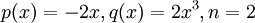 , כלומר
, כלומר ![y=\sqrt[-1]{\mathrm e^{-x^2}\left(c+\int2x^3\mathrm e^{x^2}\mathrm dx\right)}](/images/math/5/5/4/5549004f7132698f5ce562f18414cacc.png) . נציב
. נציב 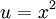 ואז
ואז 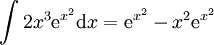 , ולבסוף
, ולבסוף 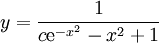 .
. 
מד״ר מדויקת
מד״ר מהצורה 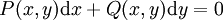 כך שקיימת
כך שקיימת 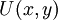 עבורה
עבורה 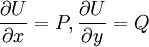 . לפיכך
. לפיכך 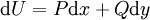 והמד״ר הופכת ל־
והמד״ר הופכת ל־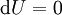 כלומר
כלומר 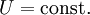 . תנאי הכרחי ומספיק לקיום
. תנאי הכרחי ומספיק לקיום 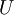 כנ״ל הוא
כנ״ל הוא 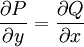 (הכרחי כי
(הכרחי כי 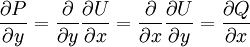 ).
).
תרגיל
פתרו 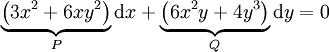 .
.
פתרון
מתקיים 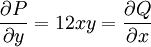 , כדרוש לקיום
, כדרוש לקיום 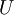 . ננסה לחשב
. ננסה לחשב 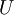 כנ"ל:
כנ"ל: 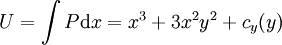 . עתה נדרוש ש־
. עתה נדרוש ש־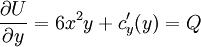 ואז
ואז 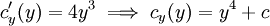 . לסיכום, פתרון המד״ר הוא
. לסיכום, פתרון המד״ר הוא 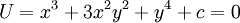 (נשים לב שניתן לבחור גם כל קבוע אחר מלבד 0, אבל שינוי כזה בסה״כ יחליף את הקבוע
(נשים לב שניתן לבחור גם כל קבוע אחר מלבד 0, אבל שינוי כזה בסה״כ יחליף את הקבוע 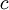 ).
). 
מד״ר לא מדויקת
תהי 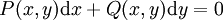 מד״ר שאינה מדויקת, ונרצה לפתור אותה ע״י גורמי אינטגרציה: ננסה להכפיל את אגפי המד״ר ב־
מד״ר שאינה מדויקת, ונרצה לפתור אותה ע״י גורמי אינטגרציה: ננסה להכפיל את אגפי המד״ר ב־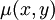 ולקבל מד״ר מדויקת
ולקבל מד״ר מדויקת 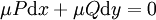 . לשם כך
. לשם כך 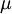 צריכה לקיים
צריכה לקיים 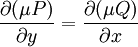 , ובאופן שקול
, ובאופן שקול 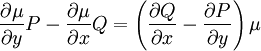 (נשים לב שזו מד״ח).
(נשים לב שזו מד״ח).
מקרה 1
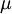 תלויה רק ב־
תלויה רק ב־ . לכן
. לכן 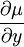 מתאפס ומכאן נובע (כאשר
מתאפס ומכאן נובע (כאשר 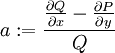 ) ש־
) ש־
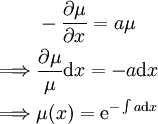
נשים לב ש־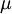 תלויה רק ב־
תלויה רק ב־ אם״ם
אם״ם  תלויה רק ב־
תלויה רק ב־ .
.
מקרה 2
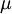 תלויה רק ב־
תלויה רק ב־ . זה מתקיים אם״ם
. זה מתקיים אם״ם 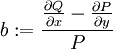 תלויה רק ב־
תלויה רק ב־ , ואז
, ואז 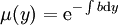 .
.
תרגיל
פתרו את המד״ר 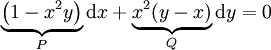 .
.
פתרון
מתקיים 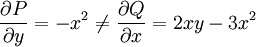 , כלומר המד״ר אינה מדויקת. נשים לב ש־
, כלומר המד״ר אינה מדויקת. נשים לב ש־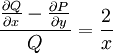 , כלומר תלויה אך ורק ב־
, כלומר תלויה אך ורק ב־ , ולכן נגדיר
, ולכן נגדיר 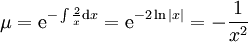 . נכפיל את אגפי המד״ר ב־
. נכפיל את אגפי המד״ר ב־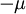 ונקבל
ונקבל 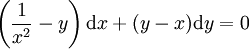 . המד״ר החדשה מקיימת
. המד״ר החדשה מקיימת 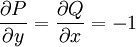 , ומכאן נוכל להמשיך לפתור כרגיל.
, ומכאן נוכל להמשיך לפתור כרגיל. 
הערה: נשים לב ש־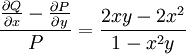 תלויה גם ב־
תלויה גם ב־ וגם ב־
וגם ב־ , ולכן הגדרת
, ולכן הגדרת 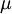 התלויה ב־
התלויה ב־ לא תועיל לנו.
לא תועיל לנו.