הבדלים בין גרסאות בדף "מדר קיץ תשעב/סיכומים/תקציר"
מתוך Math-Wiki
(יצירת דף עם התוכן "== מד״ר מסדר 1 == * מד״ר בצורה דיפרנציאלית עם משתנים מופרדים היא מהצורה <math>M_1(x)N_1(y)\mathrm dx+M_2(x)N_2(y...") |
(אין הבדלים)
|
גרסה מ־19:43, 6 באוגוסט 2012
מד״ר מסדר 1
- מד״ר בצורה דיפרנציאלית עם משתנים מופרדים היא מהצורה
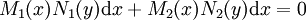 . אם
. אם 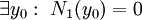 אזי
אזי 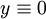 פתרון, ואם
פתרון, ואם 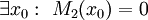 אזי
אזי 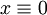 פתרון. אחרת
פתרון. אחרת 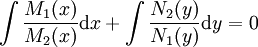 .
. - נתונה מד״ר
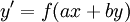 . אז נציב
. אז נציב 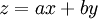 ו־
ו־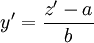 .
.
- הכללה: נתונה מד״ר
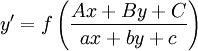 . אם
. אם 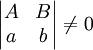 נציב
נציב 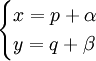 כאשר
כאשר 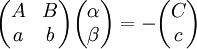 . אחרת נבחר
. אחרת נבחר 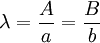 ונציב
ונציב 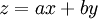 .
.
- הכללה: נתונה מד״ר
- מד״ר הומוגנית: נתונה מד״ר
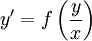 . אזי נציב
. אזי נציב 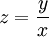 ו־
ו־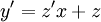 .
. - מד״ר לינארית: נתונה מד״ר
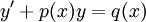 . אם היא לינארית־הומוגנית אזי
. אם היא לינארית־הומוגנית אזי 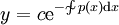 , ובכל מקרה
, ובכל מקרה 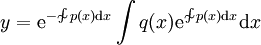 .
. - משוואת ברנולי: נתונה מד״ר
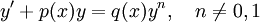 . נציב
. נציב 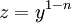 , כאשר אם
, כאשר אם 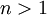 אז
אז 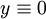 פתרון רגולרי, אם
פתרון רגולרי, אם 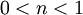 אז פתרון סינגולרי, ואם
אז פתרון סינגולרי, ואם 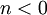 אז לא פתרון. הפתרונות הרגולריים:
אז לא פתרון. הפתרונות הרגולריים: ![y=\sqrt[1-n]{\mathrm e^{-(1-n)\sim\!\!\!\!\int p(x)\mathrm dx}\int(1-n)q(x)\mathrm e^{(1-n)\sim\!\!\!\!\int p(x)\mathrm dx}\mathrm dx}](/images/math/d/2/1/d21060ddd088f406161a14104fc4c1e8.png) .
. - מד״ר מהצורה
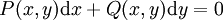 היא מדויקת אם״ם יש
היא מדויקת אם״ם יש 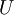 כך ש־
כך ש־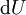 שווה לאגף ימין, מה שמתרחש אם״ם
שווה לאגף ימין, מה שמתרחש אם״ם 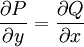 .
.
- אם המד״ר אינה מדויקת ניתן לנסות להכפיל אותה ב־
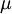 כך שתהפוך למדויקת.
כך שתהפוך למדויקת. 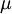 תלויה רק ב־
תלויה רק ב־ אם״ם
אם״ם 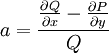 תלויה רק ב־
תלויה רק ב־ , ואז
, ואז 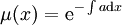 . היא תלויה רק ב־
. היא תלויה רק ב־ אם״ם
אם״ם 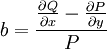 תלויה רק ב־
תלויה רק ב־ , ואז
, ואז 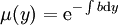 .
.
- אם המד״ר אינה מדויקת ניתן לנסות להכפיל אותה ב־
- משוואת ריקרטי: מד״ר מהצורה
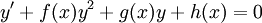 . הפתרון הכללי הוא מהצורה
. הפתרון הכללי הוא מהצורה 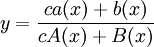 .
. - נתונה מד״ר
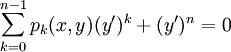 ממעלה
ממעלה  . אזי קיימות פונקציות
. אזי קיימות פונקציות 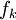 שעבורן
שעבורן 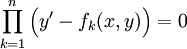 .
. - אם
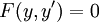 נציב
נציב 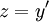 ואז
ואז 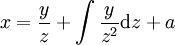 עבור
עבור  יחיד שמקיים את המד״ר. בנוסף, אם
יחיד שמקיים את המד״ר. בנוסף, אם 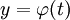 ו־
ו־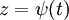 אזי
אזי 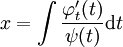 .
. - אם
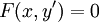 נציב
נציב 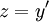 ואז
ואז 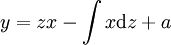 עבור
עבור  יחיד שמקיים את המד״ר. בנוסף, אם
יחיד שמקיים את המד״ר. בנוסף, אם 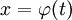 ו־
ו־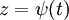 אזי
אזי 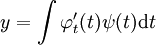 .
.
מד״ר מסדר 2
- בהנתן מד״ר
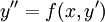 או
או 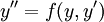 נציב
נציב 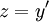 ונקבל
ונקבל 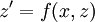 או
או 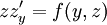 , בהתאמה. מתקיים
, בהתאמה. מתקיים 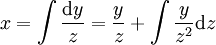 ו־
ו־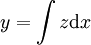 .
.