מדר קיץ תשעב/סיכומים/תרגולים/30.7.12
מתוך Math-Wiki
מיכאל קונטרונוביץ, michako (@) walla.co.il
דוגמה 1
- זהו משתנה תלוי, משתנה בלתי תלוי, סדר ומעלה עבור
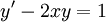 .
. - האם
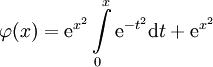 מהווה פתרון לכל
מהווה פתרון לכל 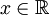 ?
?
פתרון
-
 הוא המשתנה התלוי,
הוא המשתנה התלוי,  בלתי תלוי, הסדר הוא 1 והמעלה – 1. זו משוואה לינארית.
בלתי תלוי, הסדר הוא 1 והמעלה – 1. זו משוואה לינארית. -
 גזירה כמכפלה, סכום והרכבה של פונקציות גזירות. לפי המשפט היסודי של החדו״א
גזירה כמכפלה, סכום והרכבה של פונקציות גזירות. לפי המשפט היסודי של החדו״א 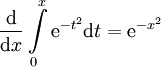 ולכן
ולכן 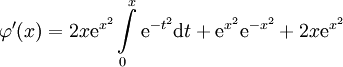 . אם נציב זאת במד״ר המקורית נגלה ש־
. אם נציב זאת במד״ר המקורית נגלה ש־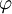 היא אכן פתרון.
היא אכן פתרון.
דוגמה 2
- פתרו את המד״ר
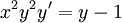 .
. - בהינתן תנאי התחלה
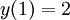 , האם יש פתרון יחיד? אם כן, מהו ומה תחום הגדרתו?
, האם יש פתרון יחיד? אם כן, מהו ומה תחום הגדרתו? - פתרו את סעיף 2 עבור תנאי ההתחלה
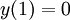 .
.
פתרון
- ננסה להפריד את המשתנים:
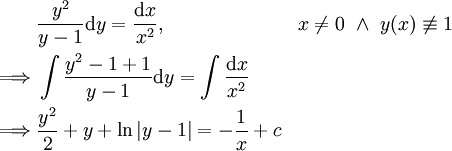
עתה נתייחס למקרה 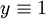 : נציב במד״ר ונקבל
: נציב במד״ר ונקבל 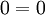 , לכן זהו אכן פתרון.
, לכן זהו אכן פתרון.
- ניעזר במשפט הקיום והיחידות לבעיית התחלה מסדר 1 (אנו נציג גרסה כללית יותר מזו שהוצגה בהרצאה, שמדברת על פונקציות רציפות ולאו דווקא ליפשיץ): נתון ש־
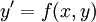 ו־
ו־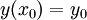 . אם קיימת סביבה פתוחה
. אם קיימת סביבה פתוחה 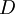 של
של 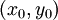 שבה
שבה 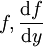 רציפות אזי יש קטע
רציפות אזי יש קטע 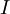 מקביל לציר
מקביל לציר  המוכל ב־
המוכל ב־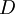 , כך שלכל
, כך שלכל 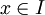 יש לבעיה פתרון יחיד. הערה: המשפט הוא תנאי מספיק ולא הכרחי לקיום יחידות.
יש לבעיה פתרון יחיד. הערה: המשפט הוא תנאי מספיק ולא הכרחי לקיום יחידות.
בחזרה לתרגיל, נגדיר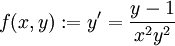 . אזי
. אזי  פונקציה רציונלית ולכן רציפה כל עוד המכנה שונה מ־0, כלומר
פונקציה רציונלית ולכן רציפה כל עוד המכנה שונה מ־0, כלומר 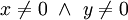 . כנ״ל עבור נגזרתה. לכן נרצה מלבן פתוח
. כנ״ל עבור נגזרתה. לכן נרצה מלבן פתוח 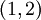 סביב נקודת ההתחלה, שאינו נוגע בצירים, למשל
סביב נקודת ההתחלה, שאינו נוגע בצירים, למשל 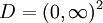 . לכן מתקיימים תנאי משפט הקיום והיחידות ולפיכך יש לבעיה פתרון יחיד.
. לכן מתקיימים תנאי משפט הקיום והיחידות ולפיכך יש לבעיה פתרון יחיד.
אם נפתור: הסינגולריות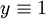 לא מקיימת את תנאי ההתחלה. נציב
לא מקיימת את תנאי ההתחלה. נציב 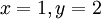 בפתרון הכללי ונקבל
בפתרון הכללי ונקבל 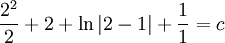 ולכן
ולכן 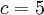 . תחום ההגדרה של
. תחום ההגדרה של 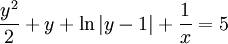 הוא
הוא 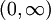 .
. - עבור
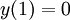 תנאי משפט הקיום והיחידות אינם מתקיימים. אין אף פתרון לבעיית ההתחלה הנ״ל – ניתן לוודא זאת בבדיקה ישירה.
תנאי משפט הקיום והיחידות אינם מתקיימים. אין אף פתרון לבעיית ההתחלה הנ״ל – ניתן לוודא זאת בבדיקה ישירה.
דוגמה 3
פתרו את המשוואה 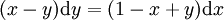 .
.
פתרון
 אינו פתרון כיוון שנובע ממנו ש־
אינו פתרון כיוון שנובע ממנו ש־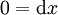 , בסתירה. נשים לב ש־
, בסתירה. נשים לב ש־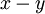 מרכזי ובלעדי במשוואה, לכן נסמנו כ־
מרכזי ובלעדי במשוואה, לכן נסמנו כ־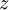 ונקבל
ונקבל 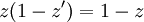 . מפני ש־
. מפני ש־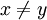 מתקיים
מתקיים 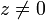 ולכן נחלק ב־
ולכן נחלק ב־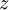 . נקבל
. נקבל 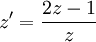 לכן (נניח ש־
לכן (נניח ש־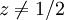 ) מתקיים
) מתקיים 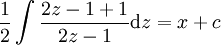 . לבסוף
. לבסוף 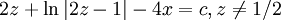 . נבדוק את
. נבדוק את 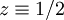 בנפרד ונגלה שהוא אכן פתרון סינגולרי.
בנפרד ונגלה שהוא אכן פתרון סינגולרי.
דוגמה 4
פתרו את בעיית ההתחלה 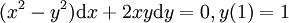 .
.
פתרון
הערה: פונקציה 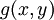 נקראת הומוגנית חיובית מסדר
נקראת הומוגנית חיובית מסדר 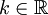 אם לכל
אם לכל 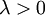 ולכל עיבוד הנוסחה נכשל (פונקציה \dom לא מוכרת): (x,y)\dom(g)
ולכל עיבוד הנוסחה נכשל (פונקציה \dom לא מוכרת): (x,y)\dom(g)
מתקיים עיבוד הנוסחה נכשל (פונקציה \g לא מוכרת): \g(\lambda x,\lambda y)=\lambda^kg(x,y)
.
כאן 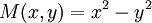 ו־
ו־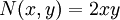 הומוגניות מסדר 2 ולכן המד״ר הומוגנית. במקרה
הומוגניות מסדר 2 ולכן המד״ר הומוגנית. במקרה 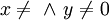 נביאה לצורה
נביאה לצורה 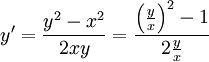 . נציב
. נציב 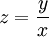 ואז
ואז 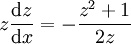 . הפתרון הכללי הוא
. הפתרון הכללי הוא 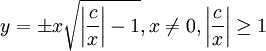 , ומתנאי ההתחלה נובע ש־
, ומתנאי ההתחלה נובע ש־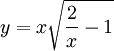 עבור
עבור 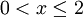 .
.