הבדלים בין גרסאות בדף "מכינה למחלקת מתמטיקה/מערכי שיעור/14"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏הוכחה בשלילה)
(←‏הכלה דו כיוונית)
שורה 64: שורה 64:
  
 
וביחד לפי הכלה דו-כיוונית <math>A=B</math>
 
וביחד לפי הכלה דו-כיוונית <math>A=B</math>
 +
 +
 +
===הוכחת פסוק עם כמתים- לכל או קיים===
 +
 +
'''דוגמא'''
 +
 +
הוכח כי לכל ממשי חיובי x קיים מספר טבעי n כך ש <math>\frac{1}{n} < x</math>
 +
 +
 +
'''הוכחת הכמת לכל''':
 +
 +
'''יהי''' מספר טבעי חיובי '''כלשהו''' x.
 +
 +
צריך למצוא מספר n כך ש <math>\frac{1}{n} < x</math>
 +
 +
 +
לכן, מספיק למצוא מספר n כך ש <math>\frac{1}{x} < n</math>
 +
 +
 +
כיוון שאין סוף למספרים הטבעיים, ניתן לבחור מספר n כלשהו הגדול מ<math>\frac{1}{x}</math>.
 +
 +
 +
 +
 +
'''דוגמא'''
 +
 +
תהי קבוצה B. הוכח כי קיימת קבוצה A שאינה ריקה כך ש <math>A\cap B = B</math>
 +
 +
 +
'''הוכחת הכמת קיים''':
 +
 +
על מנת להוכיח קיום, מספיק למצוא דוגמא אחת. למשל, אם ניקח A=B נקבל את מה שרצינו.
 +
 +
 +
'''הערה''': הוכחת קיום זו נקראת '''קונסטרוקטיבית''' כיוון שלא רק שהראנו שקיימת קבוצה בהתאם לנדרש, אלא ממש מצאנו אותה. ישנן הוכחות המוכיחות קיום מבלי למצוא דוגמא מפורשת.

גרסה מ־08:40, 30 באוגוסט 2012

שיטות הוכחה

הוכחה בשלילה

הוכחה בשלילה מבוססת על הטאוטולוגיה 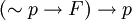(\sim p \rightarrow F)\rightarrow p. בהוכחה בשלילה אנו מניחים את השלילה של מה שצריך להוכיח ומגיעים לסתירה.

שימו לב שאנו לא שוללים את הנתון אלא את הצ"ל.


דוגמא:

תרגיל תהיינה A,B קבוצות המקיימות 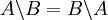A\backslash B=B\backslash A. הוכח כי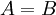 A=B


הוכחה בשלילה:


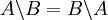
נתון: A\backslash B=B\backslash A


צ"ל: A=B


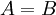
נניח בשלילה כי 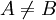A\neq B.


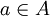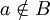לכן קיים a\in A כך ש a\notin B (או ההפך)


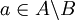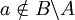לכן לפי ההגדרה a\in A\backslash B אבל a\notin B\backslash A (או ההפך)


לכן 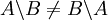A\backslash B\neq B\backslash A


בסתירה.



דוגמא. תהיינה A,B קבוצות כך ש 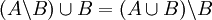(A\backslash B)\cup B = (A\cup B)\backslash B הוכח כי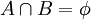 A\cap B = \phi


הכלה דו כיוונית

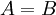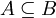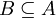
בשיטה זו אנו מוכיחים שיוויון בין קבוצות. על מנת להוכיח כי A=B מספיק להוכיח כי A\subseteq B וגם B\subseteq A


דוגמא. תהיינה קבוצות A,B המקיימות 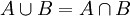A\cup B = A \cap B. הוכח כי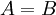 A=B


הוכחה באמצעות הכלה דו כיוונית:


מהנתון ניתן להסיק כי 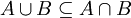A\cup B \subseteq A \cap B


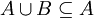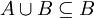
לכן בפרט A\cup B \subseteq A וגם A\cup B \subseteq B


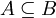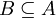
לכן A\subseteq B וגם B\subseteq A


וביחד לפי הכלה דו-כיוונית 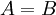A=B


הוכחת פסוק עם כמתים- לכל או קיים

דוגמא

הוכח כי לכל ממשי חיובי x קיים מספר טבעי n כך ש 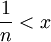\frac{1}{n} < x


הוכחת הכמת לכל:

יהי מספר טבעי חיובי כלשהו x.

צריך למצוא מספר n כך ש 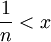\frac{1}{n} < x


לכן, מספיק למצוא מספר n כך ש 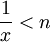\frac{1}{x} < n


כיוון שאין סוף למספרים הטבעיים, ניתן לבחור מספר n כלשהו הגדול מ\frac{1}{x}.



דוגמא

תהי קבוצה B. הוכח כי קיימת קבוצה A שאינה ריקה כך ש 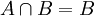A\cap B = B


הוכחת הכמת קיים:

על מנת להוכיח קיום, מספיק למצוא דוגמא אחת. למשל, אם ניקח A=B נקבל את מה שרצינו.


הערה: הוכחת קיום זו נקראת קונסטרוקטיבית כיוון שלא רק שהראנו שקיימת קבוצה בהתאם לנדרש, אלא ממש מצאנו אותה. ישנן הוכחות המוכיחות קיום מבלי למצוא דוגמא מפורשת.

מקור: https://math-wiki.com/index.php?title=מכינה_למחלקת_מתמטיקה/מערכי_שיעור/14&oldid=26551