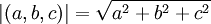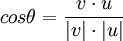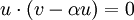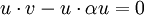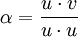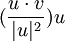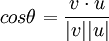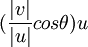מכינה למחלקת מתמטיקה/מערכי שיעור/6

חזרה למערכי השיעור

וקטורים

באופן דומה למישור המרוכב, וקטור ניתן להצגה בשתי דרכים: גאומטרית ואלגברית. אלגברית, וקטור הוא נקודה כללית במרחב 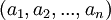$(a_1,a_2,...,a_n)$. גאומטרית, וקטור הוא שילוב של אורך וכיוון.

באופן גיאומטרי, החיבור בין שני וקטורים הוא אלכסון המקבילית הנוצרת בינהן. מבחינה אלגברית 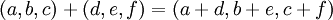$(a,b,c)+(d,e,f)=(a+d,b+e,c+f)$

כל וקטור במישור ניתן לפירוק לרכיבים שלו על כל אחד מהצירים, זה שקול למעבר מהצורה הפולרית לצורה הקרטזית. פירוק זה משמש אותנו בעיקר בפיסיקה, כאשר אנו מעוניינים לדעת כיצד כוח בזוית מסויימת משפיע על גוף בזוית אחרת- למשל כיצד כוח המשיכה משפיע על קרונית במדרון, מהי הזוית הטובה ביותר לזרוק כדור למרחק וכדומה.

הגדרות:

• אורך וקטור (לפי פיתגורס) הוא

$|(a,b,c)|=\sqrt{a^2+b^2+c^2}$

זהו למעשה מרחק הנקודה במרחב מראשית הצירים.

• המרחק בין שני וקטורים v,u הוא $|v-u|$

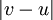
• המכפלה הסקלרית בין שני וקטורים היא $(a,b,c)\cdot(x,y,z)=ax+by+cz$.

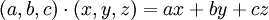• מכפלה בקבוע מוגדרת על ידי $\alpha(x,y,z)=(\alpha x,\alpha y,\alpha z)$

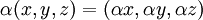
• הזוית בין שני הוקטורים במישור v,u מקיימת

$cos\theta = \frac{v\cdot u}{|v|\cdot |u|}$

• המכפלה הוקטורית בין שני וקטורים במרחב היא $(a,b,c)\cdot(x,y,z)=(bz-cy,cx-az,ay-bx)$

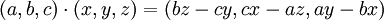
תרגילים

• הוכח כי שני וקטורים במישור מאונכים זה לזה אם"ם המכפלה הסקלרית בינהם היא אפס.

הערה: הדבר נכון גם לוקטורים במרחב.

• הוכח כי $|v|=\sqrt{v\cdot v}$

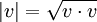
• הוכח כי כפל בקבוע משנה את האורך באופן הבא: 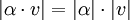$|\alpha\cdot v|=|\alpha|\cdot |v|$ (שימו לב שזה הערך המוחלט של הקבוע, כפול אורך הוקטור).

• הוכח כי לכל שלושה וקטורים וקבוע מתקיים $(u+\alpha v)\cdot w=u\cdot w+\alpha v\cdot w$

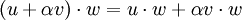
• הוכח את אי שיוויון המשולש לוקטורים במרחב $|u+v|\leq |u|+|v|$

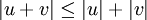
• הוכח כי המכפלה הוקטורית בין שני וקטורים v,u מאונכת גם לv וגם לu (באמצעות המכפלה הפנימית)

היטל

היטל של וקטור v על קו ישר הנפרש על ידי וקטור u הינו וקטור על הקו הישר (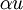$\alpha u$) כך שההפרש 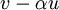$v-\alpha u$ מאונך לישר.

מבחינה גיאומטרית, ההיטל הוא הנקודה הקרובה ביותר לוקטור v על הישר.

מבחינה פיזיקלית, ההיטל הוא הרכיב של v בכיוון הישר.

נמצא נוסחא להיטל. דרשנו כי ההפרש בין הוקטור להיטל יהיה מאונך לישר, לכן:

$u\cdot (v-\alpha u) = 0$

$u\cdot v - u\cdot\alpha u = 0$

$\alpha = \frac{u\cdot v}{u\cdot u}$

ולכן ההיטל של v על הישר הנפרש על ידי הוקטור u הינו:

$(\frac{u\cdot v}{|u|^2})u$

מצד שני, אנו יודעים כי הזוית בין v לu מקיימת

$cos\theta = \frac{v\cdot u}{|v||u|}$

ולכן אנו מקבלים נוסחא שניה להיטל המזכירה את הפירוק הפיסיקלי לרכיבים:

$(\frac{|v|}{|u|}cos\theta) u$