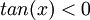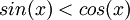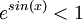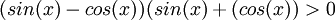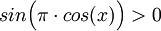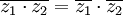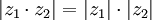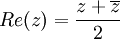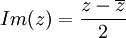הבדלים בין גרסאות בדף "מכינה למתמטיקה קיץ תשעב/תרגילים/2/פתרון 2"
מתוך Math-Wiki
Tomer Yogev (שיחה | תרומות) (←1) |
Tomer Yogev (שיחה | תרומות) |
||
| שורה 27: | שורה 27: | ||
עבור <math>k=0</math>: אי השוויון הוא <math>0<cos(x)<1</math> וזה מתקיים לכל <math>-{\pi \over 2}+2\pi k < x < {\pi \over 2} + 2\pi k</math> | עבור <math>k=0</math>: אי השוויון הוא <math>0<cos(x)<1</math> וזה מתקיים לכל <math>-{\pi \over 2}+2\pi k < x < {\pi \over 2} + 2\pi k</math> | ||
| + | |||
| + | |||
| + | ==2== | ||
| + | הוכח: | ||
| + | |||
| + | *<math>\overline{z_1\cdot z_2}=\overline{z_1}\cdot\overline{z_2}</math> | ||
| + | |||
| + | |||
| + | *<math>|z_1\cdot z_2| = |z_1|\cdot |z_2|</math> | ||
| + | |||
| + | |||
| + | *<math>Re(z)= \frac{z+\overline{z}}{2}</math> | ||
| + | |||
| + | |||
| + | *<math>Im(z)= \frac{z-\overline{z}}{2}</math> | ||
גרסה מ־01:57, 13 באוגוסט 2012
1
מצא לאילו ערכי x מתקיימים אי השיוויונים הבאים:
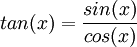 לכן אי השוויון מתקיים כאשר למונה ולמכנה יש סימנים הפוכים. לפי הגדרת הפונקציות הטריגונומטריות בעזרת מעגל היחידה, ניתן לראות שזה מתקיים ברביע השני וברביע הרביעי, ולכן התשובה היא:
לכן אי השוויון מתקיים כאשר למונה ולמכנה יש סימנים הפוכים. לפי הגדרת הפונקציות הטריגונומטריות בעזרת מעגל היחידה, ניתן לראות שזה מתקיים ברביע השני וברביע הרביעי, ולכן התשובה היא: 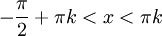
מתקיים שוויון כאשר 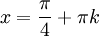 . עד
. עד 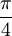 הקוסינוס יותר גדול, ובנקודה זו זה מתהפך עד
הקוסינוס יותר גדול, ובנקודה זו זה מתהפך עד 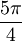 בה זה מתהפך בחזרה, וכך ממשיך במחזוריות של
בה זה מתהפך בחזרה, וכך ממשיך במחזוריות של 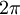 . לכן אי השוויון מתקיים עבור
. לכן אי השוויון מתקיים עבור 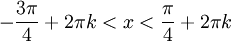
נסמן 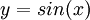 ונבדוק מתי
ונבדוק מתי 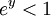 . יש שוויון עבור y=0 לכן אי השוויון מתקיים עבור
. יש שוויון עבור y=0 לכן אי השוויון מתקיים עבור 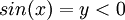 . מתכונות סינוס, זה מתקיים עבור
. מתכונות סינוס, זה מתקיים עבור 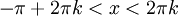
נפתח סוגריים ונקבל: 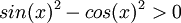 . ניעזר בזהות
. ניעזר בזהות 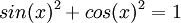 ונגיע לאי השוויון:
ונגיע לאי השוויון: 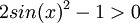 . מכאן נעביר אגפים ונקבל
. מכאן נעביר אגפים ונקבל 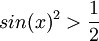 והפתרון שלו הוא
והפתרון שלו הוא 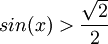 או
או 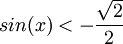 . זה מתקיים עבור:
. זה מתקיים עבור: 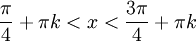
נציב 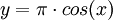 ונקבל שאי השוויון מתקיים עבור
ונקבל שאי השוויון מתקיים עבור 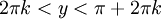 . לכן
. לכן 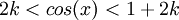 .
.
אם 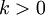 : נקבל
: נקבל 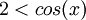 וזה לא יתכן.
וזה לא יתכן.
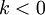 : נקבל
: נקבל 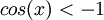 וזה גם לא יתכן.
וזה גם לא יתכן.
עבור 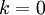 : אי השוויון הוא
: אי השוויון הוא 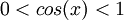 וזה מתקיים לכל
וזה מתקיים לכל 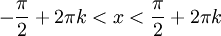
2
הוכח: