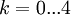הבדלים בין גרסאות בדף "מכינה למתמטיקה קיץ תשעב/תרגילים/3/פתרון 3"
מתוך Math-Wiki
Tomer Yogev (שיחה | תרומות) (יצירת דף עם התוכן "==1== * חשב את הסכום <math>1+\frac{sin(1)}{2} + \frac{sin(2)}{4}+\frac{sin(3)}{8}+...+\frac{sin(n)}{2^n}</math> ['''רמז''': סכום סדרה הנדס...") |
Tomer Yogev (שיחה | תרומות) (←1) |
||
| שורה 4: | שורה 4: | ||
['''רמז''': סכום סדרה הנדסית <math>1+q+...+q^{n} = \frac{1-q^{n+1}}{1-q}</math>, ומשפט דה-מואבר] | ['''רמז''': סכום סדרה הנדסית <math>1+q+...+q^{n} = \frac{1-q^{n+1}}{1-q}</math>, ומשפט דה-מואבר] | ||
| + | נסמן <math>z=\frac{cis(1)}{2}</math> | ||
| + | |||
| + | לפי דה מואבר: <math>z^n = \frac{cis(n)}{2^n}</math> | ||
| + | |||
| + | לכן: <math>1+z+...+z^n = 1+\frac{cis(1)}{2} + ... + \frac{cis(n)}{2^n}= \Big(1+\frac{cos(1)}{2} + ... + \frac{cos(n)}{2^n} \Big)+i \cdot \Big(1+\frac{ sin(1)}{2} + ... + \frac{sin(n)}{2^n} \Big)</math> | ||
| + | |||
| + | לכן הסכום המבוקש שווה <math>Im(1+z+...+z^n)</math>. נחשב: | ||
| + | |||
| + | <math>Im(1+z+...+z^n)=Im(\frac{1-z^{n+1}}{1-z})=Im(\frac{1-\frac{cis(n+1)}{2^{n+1}}}{1-\frac{cis(1)}{2}})</math> | ||
| + | |||
| + | |||
| + | בשלב זה ניתן לכפול בצמוד של המכנה, לפשט את הביטוי ולקבל את החלק המדומה שהוא התשובה הסופית: <math>\frac{\frac{sin(n)}{2^n}-\frac{sin(n+1)}{2^{n-1}}+2sin(1)}{5-4cos(1)}</math> | ||
* מצא את כל הפתרונות של המשוואה <math>z^5=1-i</math> | * מצא את כל הפתרונות של המשוואה <math>z^5=1-i</math> | ||
| + | |||
| + | נמצא את ההצגה הפולארית של <math>1-i</math>: | ||
| + | |||
| + | <math>r=\sqrt{1^2+1^2}=\sqrt{2}</math> | ||
| + | |||
| + | <math>\varphi=arctan(-1/1)=-\frac{\pi}{4}</math> | ||
| + | |||
| + | לכן המשוואה היא: <math>z^5=\sqrt{2} \cdot cis(-\frac{\pi}{4}+2\pi k)</math> | ||
| + | |||
| + | לכן לפי דה מואבר נקבל: <math>z=\sqrt[10]{2} \cdot cis(-\frac{\pi}{20} + \frac{2\pi k}{5})</math> | ||
| + | |||
| + | הפתרונות מתקבלים כאשר נציב <math>k=0...4</math> | ||
גרסה מ־03:12, 15 באוגוסט 2012
1
- חשב את הסכום
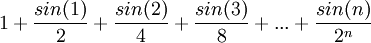
[רמז: סכום סדרה הנדסית 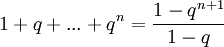 , ומשפט דה-מואבר]
, ומשפט דה-מואבר]
נסמן 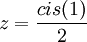
לפי דה מואבר: 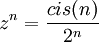
לכן: 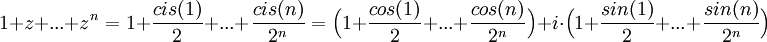
לכן הסכום המבוקש שווה 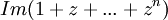 . נחשב:
. נחשב:
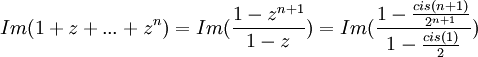
בשלב זה ניתן לכפול בצמוד של המכנה, לפשט את הביטוי ולקבל את החלק המדומה שהוא התשובה הסופית: 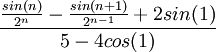
- מצא את כל הפתרונות של המשוואה
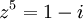
נמצא את ההצגה הפולארית של 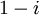 :
:
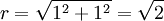
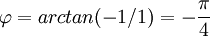
לכן המשוואה היא: 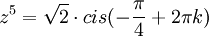
לכן לפי דה מואבר נקבל: ![z=\sqrt[10]{2} \cdot cis(-\frac{\pi}{20} + \frac{2\pi k}{5})](/images/math/6/7/d/67d517d09345b8d4558b8feead8f8589.png)
הפתרונות מתקבלים כאשר נציב