מכינה למתמטיקה קיץ תשעב/תרגילים/3/פתרון 3

1

• חשב את הסכום $1+\frac{sin(1)}{2} + \frac{sin(2)}{4}+\frac{sin(3)}{8}+...+\frac{sin(n)}{2^n}$

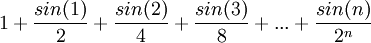
[רמז: סכום סדרה הנדסית 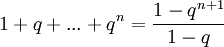$1+q+...+q^{n} = \frac{1-q^{n+1}}{1-q}$, ומשפט דה-מואבר]

נסמן 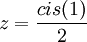$z=\frac{cis(1)}{2}$

לפי דה מואבר: 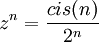$z^n = \frac{cis(n)}{2^n}$

לכן: $1+z+...+z^n = 1+\frac{cis(1)}{2} + ... + \frac{cis(n)}{2^n}= \Big(1+\frac{cos(1)}{2} + ... + \frac{cos(n)}{2^n} \Big)+i \cdot \Big(1+\frac{ sin(1)}{2} + ... + \frac{sin(n)}{2^n} \Big)$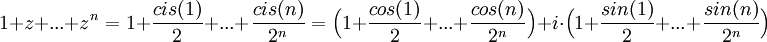

לכן הסכום המבוקש שווה 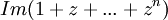$Im(1+z+...+z^n)$. נחשב:

$Im(1+z+...+z^n)=Im(\frac{1-z^{n+1}}{1-z})=Im(\frac{1-\frac{cis(n+1)}{2^{n+1}}}{1-\frac{cis(1)}{2}})$

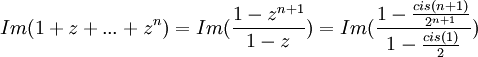
בשלב זה ניתן לכפול בצמוד של המכנה, לפשט את הביטוי ולקבל את החלק המדומה שהוא התשובה הסופית: 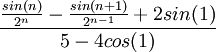$\frac{\frac{sin(n)}{2^n}-\frac{sin(n+1)}{2^{n-1}}+2sin(1)}{5-4cos(1)}$

• מצא את כל הפתרונות של המשוואה $z^5=1-i$

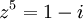
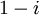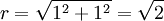
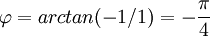
נמצא את ההצגה הפולארית של $1-i$:

$r=\sqrt{1^2+1^2}=\sqrt{2}$

$\varphi=arctan(-1/1)=-\frac{\pi}{4}$

לכן המשוואה היא: 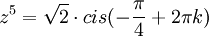$z^5=\sqrt{2} \cdot cis(-\frac{\pi}{4}+2\pi k)$

לכן לפי דה מואבר נקבל: $z=\sqrt[10]{2} \cdot cis(-\frac{\pi}{20} + \frac{2\pi k}{5})$

הפתרונות מתקבלים כאשר נציב 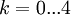$k=0...4$

2

• מצא את ההיטל של הוקטור 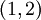$(1,2)$ על הישר הנפרש על ידי הוקטור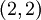 $(2,2)$

נסמן את הוקטור הרצוי ב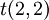$t(2,2)$. השיפוע של הישר הוא 1 לכן השיפוע של הישר המאונך הוא $-1$.

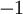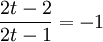$\frac{2t-2}{2t-1} = -1$. נפתור ונקבל 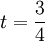$t=\frac{3}{4}$. נציב ונקבל: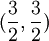 $(\frac{3}{2},\frac{3}{2})$

• מצא וקטור המתחיל בראשית בצירים ומאונך לישר שמשוואתו $3x-1=y$

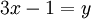
• מצא וקטור מאונך למישור הנפרש על ידי שני הוקטורים $(1,2,3),(1,4,5)$

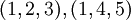
• מצא וקטור מאורך אחד, בכיוון הוקטור $(1,2,2)$

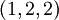
• מצא נוסחא כללית לוקטור מאורך אחד בכיוון הוקטור $u$

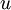
• מצא את משוואת המישור המאונך לוקטור 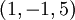$(1,-1,5)$ ועובר בנקודה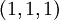 $(1,1,1)$

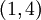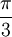• מצא את כל הוקטורים מאורך אחד אשר הזוית בינם לבין הוקטור $(1,4)$ הינה $\frac{\pi}{3}$. כמה כאלה יש?

• הוכח עבור וקטורים במישור כי מתקיים אי השיוויון 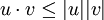$u\cdot v \leq |u||v|$ (ישירות לפי ההגדרה של מכפלה סקלרית ואורך וקטור).

[רמז: השתמש בזהות הידועה 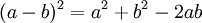$(a-b)^2 = a^2+b^2-2ab$]