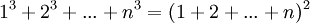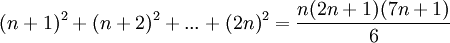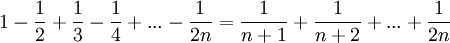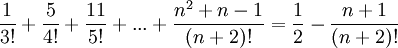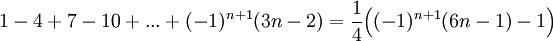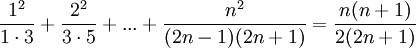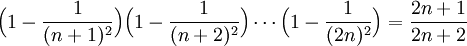מכינה למתמטיקה קיץ תשעב/תרגילים/4/פתרון 4

בכל התרגילים צריך לבדוק גם את המקרה ההתחלתי עבור n=1 אבל דילגתי על זה כי זה פשוט. בכולם אני מניח שהטענה נכונה עבור n ומוכיח שמכך נובע שהיא נכונה גם עבור n+1.

תרגילים - שיוויונים

• $1^3+2^3+...+n^3=(1+2+...+n)^2$

• $(n+1)^2+(n+2)^2+...+(2n)^2=\frac{n(2n+1)(7n+1)}{6}$

• $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...-\frac{1}{2n}=\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{2n}$

• $\frac{1}{3!}+\frac{5}{4!}+\frac{11}{5!}+...+\frac{n^2+n-1}{(n+2)!}=\frac{1}{2}-\frac{n+1}{(n+2)!}$

• $1-4+7-10+...+(-1)^{n+1}(3n-2)=\frac{1}{4}\Big((-1)^{n+1}(6n-1)-1\Big)$

• $\frac{1^2}{1\cdot 3}+\frac{2^2}{3\cdot 5}+...+\frac{n^2}{(2n-1)(2n+1)}=\frac{n(n+1)}{2(2n+1)}$

• $\Big(1-\frac{1}{(n+1)^2}\Big)\Big(1-\frac{1}{(n+2)^2}\Big)\cdots \Big(1-\frac{1}{(2n)^2}\Big)=\frac{2n+1}{2n+2}$