משפט ערך הביניים
משפט ערך הביניים
תהי  פונקציה הרציפה בקטע [a,b]. אזי לכל
פונקציה הרציפה בקטע [a,b]. אזי לכל 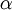 בין
בין 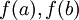 קיימת
קיימת ![c\in[a,b]](/images/math/0/0/a/00a49aece4cc72157b51ca282347a0f8.png) כך ש
כך ש 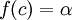
הוכחה
ראשית, נוכיח משפט חלש יותר:
תהי  פונקציה הרציפה בקטע [a,b]. אזי אם
פונקציה הרציפה בקטע [a,b]. אזי אם 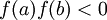 קיימת
קיימת ![c\in[a,b]](/images/math/0/0/a/00a49aece4cc72157b51ca282347a0f8.png) כך ש
כך ש 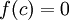
כלומר, פונקציה רציפה חייבת להתאפס בין נקודה בה היא מקבלת ערך שלילי לבין נקודה בה היא מקבלת ערך חיובי. (היא לא יכול "לדלג" על ציר x.)
הוכחה.
נגדיר ![I_1=[a,b]](/images/math/2/3/7/237107e5166d7e5c4b71c0985b013ac0.png) . כעת, אם
. כעת, אם 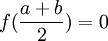 סיימנו.
סיימנו.
אחרת, נחלק את הקטע לשניים, וניקח ![I_2=[a,\frac{a+b}{2}]](/images/math/7/2/0/7202edb3d5549ecf7e686db05a73a576.png) או
או ![I_2=[\frac{a+b}{2},b]](/images/math/f/4/2/f42bf1d1532d3a41126cc864604b2dcb.png) כך שהפונקציה תקבל סימנים מנוגדים בקצות הקטע.
כך שהפונקציה תקבל סימנים מנוגדים בקצות הקטע.
נחלק שוב את הקטע באופן דומה עד שנקבל נקודה בה הפונקציה מתאפסת, או שנקבל סדרה של קטעים המוכלים זה בזה, בעלי אורך שואף לאפס (שכן אנחנו מחלקים את האורך בשתים כל פעם).
אם קיבלנו סדרה אינסופית של קטעים ![I_n=[a_n,b_n]](/images/math/8/9/6/896f17899a5f55ed35de918753570d00.png) , היא מקיימת את הלמה של קנטור ויש נקודת גבול משותפת
, היא מקיימת את הלמה של קנטור ויש נקודת גבול משותפת ![\lim a_n = \lim b_n = c\in [a,b]](/images/math/b/0/5/b05d4d973047dd4c962a767c6f21a5a1.png)
כעת, כיוון שהפונקציה רציפה, לפי היינה
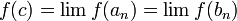 . אבל כיוון שהפונקציה מקבל אינסוף ערכים שליליים על סדרות אלה, וגם אינסוף ערכים חיוביים, הגבול חייב להיות אפס, כלומר
. אבל כיוון שהפונקציה מקבל אינסוף ערכים שליליים על סדרות אלה, וגם אינסוף ערכים חיוביים, הגבול חייב להיות אפס, כלומר
כפי שרצינו.
כעת נחזור למקרה הכללי. נביט בפונקציה 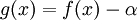 . כיוון ש
. כיוון ש 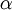 בין
בין 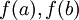 ברור כי
ברור כי
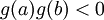 .
.
לפי המשפט לעיל, קיימת c בקטע כך ש 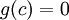 כלומר,
כלומר, 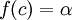 כפי שרצינו.
כפי שרצינו.