הבדלים בין גרסאות בדף "משתמש:אור שחף/עבודה ב"שימושי המתמטיקה ביומיום""
מ |
|||
| שורה 1: | שורה 1: | ||
| − | |||
באי מסוים כל התושבים הם או אבירים, הדוברים תמיד אמת, או נוכלים, אשר תמיד משקרים. בחלק מהבעיות מוסיפים סוג נוסף – מרגלים, שעונים אמת או שקר באקראי. החידות דנות באורח באי המנסה להסיק מספר מסקנות – לרוב את הסוג של כמה מהתושבים – על סמך כמה עובדות (שמרביתן מהצורה "תושב <math>X</math> טען ש־<math>P</math>") ו/או על סמך שאלות כן/לא שעליו לשאול. | באי מסוים כל התושבים הם או אבירים, הדוברים תמיד אמת, או נוכלים, אשר תמיד משקרים. בחלק מהבעיות מוסיפים סוג נוסף – מרגלים, שעונים אמת או שקר באקראי. החידות דנות באורח באי המנסה להסיק מספר מסקנות – לרוב את הסוג של כמה מהתושבים – על סמך כמה עובדות (שמרביתן מהצורה "תושב <math>X</math> טען ש־<math>P</math>") ו/או על סמך שאלות כן/לא שעליו לשאול. | ||
| שורה 8: | שורה 7: | ||
== חידות ללא מרגלים == | == חידות ללא מרגלים == | ||
| − | {| class="wikitable" style="direction:ltr; float:left; margin-top: 0;" | + | {| class="wikitable" style="direction:ltr; float:left; margin-top:0;" |
! <math>P</math> !! <math>Q</math> !! <math>P\leftrightarrow Q</math> | ! <math>P</math> !! <math>Q</math> !! <math>P\leftrightarrow Q</math> | ||
|- | |- | ||
| שורה 19: | שורה 18: | ||
| 1 || 1 || 1 | | 1 || 1 || 1 | ||
|} | |} | ||
| − | באלגברה בוליאנית מסמנים <math>1</math> כפסוק אמת ו־<math>0</math> כפסוק שקר | + | באלגברה בוליאנית מסמנים <math>1</math> כפסוק אמת ו־<math>0</math> כפסוק שקר. נעזר בסימון <math>\leftrightarrow</math> לציון אופרטור שקילות לוגית, המוגדר כמפורט בטבלה שמשמאל. <math>=</math> הוא יחס שקילות בין כל שני פסוקים שקולים לוגית, כלומר אם ידוע ש־<math>P\leftrightarrow Q</math> נותן 1 אז נוכל לסמן <math>P=Q</math>. אם תושב <math>X</math> הוא אביר אז נסמן <math>X=1</math> ואם נוכל – <math>X=0</math>. לפיכך, אם <math>X</math> טוען טענה <math>P</math> אז <math>X=P</math>. |
| − | '''דוגמה 1.1:''' באמצעות סימונים אלו נציג את ''דוגמה 1'' כמערכת משוואות בוליאניות. <math>A</math> טוען ש־<math>B,C</math> מאותו סוג, כלומר הוא טוען <math>B\leftrightarrow C</math>. מכך נובעת משוואה (1) במערכת המשוואות הבאה. מהטענות של <math>B,C</math> נובעות המשוואות (2) ו־(3), ומהעובדה ש־<math>A,C</math> שונים נובעת משוואה (4): | + | :'''דוגמה 1.1:''' באמצעות סימונים אלו נציג את ''דוגמה 1'' כמערכת משוואות בוליאניות. <math>A</math> טוען ש־<math>B,C</math> מאותו סוג, כלומר הוא טוען <math>B\leftrightarrow C</math>. מכך נובעת משוואה (1) במערכת המשוואות הבאה. מהטענות של <math>B,C</math> נובעות המשוואות (2) ו־(3), ומהעובדה ש־<math>A,C</math> שונים נובעת משוואה (4): |
{{left|<math>\begin{array}{llcl} | {{left|<math>\begin{array}{llcl} | ||
| − | (1)&A\leftrightarrow B\leftrightarrow C& | + | (1)&A\leftrightarrow B\leftrightarrow C&=&1\\ |
| − | (2)&B\leftrightarrow A\leftrightarrow1& | + | (2)&B\leftrightarrow A\leftrightarrow1&=&1\\ |
| − | (3)&C\leftrightarrow C\leftrightarrow D& | + | (3)&C\leftrightarrow C\leftrightarrow D&=&1\\ |
| − | (4)&A\leftrightarrow C& | + | (4)&A\leftrightarrow C&=&0\end{array}</math>}} |
| − | באופן שקול: | + | :באופן שקול: |
{{left|<math>\begin{array}{llcl} | {{left|<math>\begin{array}{llcl} | ||
| − | (1)&A\nleftrightarrow B\nleftrightarrow C& | + | (1)&A\nleftrightarrow B\nleftrightarrow C&=&1\\ |
| − | (2)&A\nleftrightarrow B& | + | (2)&A\nleftrightarrow B&=&0\\ |
| − | (3)&D& | + | (3)&D&=&1\\ |
| − | (4)&A\nleftrightarrow C& | + | (4)&A\nleftrightarrow C&=&1\end{array}</math>}} |
| − | כאשר <math>\nleftrightarrow</math> מציין אופרטור XOR, המסומן גם כ־<math>\oplus</math>. | + | :כאשר <math>\nleftrightarrow</math> מציין אופרטור XOR, המסומן גם כ־<math>\oplus</math>. |
| − | בסימונים אלו נגדיר ''עובדה'' בתור משוואה בוליאנית שנתונה בחידה, כגון <math>A\leftrightarrow C | + | בסימונים אלו נגדיר ''עובדה'' בתור משוואה בוליאנית שנתונה בחידה, כגון <math>A\leftrightarrow C=0</math> מ''דוגמה 1''. |
=== חידות ללא שאלות === | === חידות ללא שאלות === | ||
==== פתרון כמערכת משוואות ==== | ==== פתרון כמערכת משוואות ==== | ||
| − | ברגע שיש לנו ניסוח מתמטי של החידה כמערכת משוואות | + | ברגע שיש לנו ניסוח מתמטי של החידה כמערכת משוואות אפשר לפתור אותה. אנו נתעמק בחידות שניתן לפתור כמערכת משוואות לינאריות כיוון שהן נותנות מידע רב יותר על החידה, כפי שנראה בהמשך. |
ניצור איזומורפיזם מהשדה <math>(\mathbb Z_2,+,\cdot)</math> ל־<math>(\{0,1\},\nleftrightarrow,\and)</math> ע״י <math>x\mapsto\begin{cases}0,&x=[0]_2\\1,&x=[1]_2\end{cases}</math>. מכך נובע ש־<math>(\{0,1\},\nleftrightarrow,\and)</math> שדה. סכום <math>\sum_{i=1}^m P_i</math> (כאשר <math>\forall i:\ P_i\in\{0,1\}</math>) יוגדר בתור <math>P_1\nleftrightarrow\dots\nleftrightarrow P_m</math> ומכפלה <math>\prod_{i=1}^m P_i</math> בתור <math>P_1\and\dots\and P_m</math>. גם כפל מטריצות מוגדר בהתאם. | ניצור איזומורפיזם מהשדה <math>(\mathbb Z_2,+,\cdot)</math> ל־<math>(\{0,1\},\nleftrightarrow,\and)</math> ע״י <math>x\mapsto\begin{cases}0,&x=[0]_2\\1,&x=[1]_2\end{cases}</math>. מכך נובע ש־<math>(\{0,1\},\nleftrightarrow,\and)</math> שדה. סכום <math>\sum_{i=1}^m P_i</math> (כאשר <math>\forall i:\ P_i\in\{0,1\}</math>) יוגדר בתור <math>P_1\nleftrightarrow\dots\nleftrightarrow P_m</math> ומכפלה <math>\prod_{i=1}^m P_i</math> בתור <math>P_1\and\dots\and P_m</math>. גם כפל מטריצות מוגדר בהתאם. | ||
| − | כעת, אם התושבים הם <math>X_1,\dots,X_n</math> אז נסמן <math>\mathbf x:=\begin{pmatrix}X_1\\\vdots\\X_n\end{pmatrix}</math>. אם כל <math>P_i</math> מייצג נעלם <math>X_j</math> או קבוע <math>1,0</math> אז נוכל להציג כל <math>P_1\ | + | כעת, אם התושבים הם <math>X_1,\dots,X_n</math> אז נסמן <math>\mathbf x:=\begin{pmatrix}X_1\\\vdots\\X_n\end{pmatrix}</math>. אם כל <math>P_i</math> מייצג נעלם <math>X_j</math> או קבוע <math>1,0</math> אז נוכל להציג כל <math>P_1\leftrightarrow\dots\leftrightarrow P_n=P_{n+1}</math> בתור סכום של נעלמים שונים השווה לקבוע: לדוגמה, <math>B\leftrightarrow A\leftrightarrow1=1</math> מהניסוח המתמטי של ''דוגמה 1'' שקול ל־<math>A\nleftrightarrow B=0</math>, כלומר ל־<math>\sum_{X_i\in\{A,B\}}X_i=0</math>. לכן נוכל להגדיר מטריצת מקדמים <math>\mathbf A</math> ווקטור מקדמים חופשיים <math>\mathbf b</math> כך ש־<math>\mathbf{Ax}=\mathbf b</math>. |
| − | '''דוגמה 1.2:''' ההצגה המטריציונית של ''דוגמה 1'' היא | + | :'''דוגמה 1.2:''' ההצגה המטריציונית של ''דוגמה 1'' היא |
| − | {{left|<math>\underbrace\begin{pmatrix}1&1&1&0\\1&1&0&0\\0&0&0&1\\1&0&1&0\end{pmatrix}_\mathbf A\underbrace\begin{pmatrix}A\\B\\C\\D\end{pmatrix}_\mathbf x | + | {{left|<math>\underbrace\begin{pmatrix}1&1&1&0\\1&1&0&0\\0&0&0&1\\1&0&1&0\end{pmatrix}_\mathbf A\underbrace\begin{pmatrix}A\\B\\C\\D\end{pmatrix}_\mathbf x=\underbrace\begin{pmatrix}1\\0\\1\\1\end{pmatrix}_\mathbf b</math>}} |
הצגה זו מאפשרת לנו למצוא מה הסוג של כל תושב ע״י פתרון מערכת משוואות לינאריות. יתרה מזאת, לפי משפט רושה–קפלי (Rouché–Capelli) יש פתרון ל־<math>\mathbf{Ax}=\mathbf b</math> אם״ם <math>\mathbf b\in\operatorname{span}\left\{\operatorname{Col}_i(\mathbf A)\right\}_{i=1}^n</math> כאשר <math>\operatorname{Col}_i(\mathbf A)</math> העמודה ה־<math>i</math> של <math>\mathbf A</math>, ואם כן אז מרחב הפתרונות הוא ממימד <math>n-\operatorname{rank}(\mathbf A)</math>. מכאן נובע שאנו יכולים לבדוק האם קיים פתרון לחידה, ואם כן לחשב את מספר הפתרונות בתור <math>2^{n-\operatorname{rank}(\mathbf A)}</math>. מובן שבד״כ יש רק פתרון אחד, כלומר <math>\mathbf A</math> הפיכה. | הצגה זו מאפשרת לנו למצוא מה הסוג של כל תושב ע״י פתרון מערכת משוואות לינאריות. יתרה מזאת, לפי משפט רושה–קפלי (Rouché–Capelli) יש פתרון ל־<math>\mathbf{Ax}=\mathbf b</math> אם״ם <math>\mathbf b\in\operatorname{span}\left\{\operatorname{Col}_i(\mathbf A)\right\}_{i=1}^n</math> כאשר <math>\operatorname{Col}_i(\mathbf A)</math> העמודה ה־<math>i</math> של <math>\mathbf A</math>, ואם כן אז מרחב הפתרונות הוא ממימד <math>n-\operatorname{rank}(\mathbf A)</math>. מכאן נובע שאנו יכולים לבדוק האם קיים פתרון לחידה, ואם כן לחשב את מספר הפתרונות בתור <math>2^{n-\operatorname{rank}(\mathbf A)}</math>. מובן שבד״כ יש רק פתרון אחד, כלומר <math>\mathbf A</math> הפיכה. | ||
| − | '''דוגמה 1.3:''' נפתור את ''דוגמה 1''. חישוב פשוט מראה ש־<math>\mathbf A</math> הפיכה (ומכאן שיש פתרון יחיד) ו־<math>\mathbf A^{-1} | + | :'''דוגמה 1.3:''' נפתור את ''דוגמה 1''. חישוב פשוט מראה ש־<math>\mathbf A</math> הפיכה (ומכאן שיש פתרון יחיד) ו־<math>\mathbf A^{-1}=\begin{pmatrix}1&1&0&1\\1&0&0&1\\1&1&0&0\\0&0&1&0\end{pmatrix}</math>. לכן <math>\mathbf x=\mathbf A^{-1}\mathbf b=\begin{pmatrix}0\\0\\1\\1\end{pmatrix}</math> – התושבים <math>A,B</math> נוכלים ו־<math>C,D</math> אבירים. |
==== פתרון באמצעות ניחוש ==== | ==== פתרון באמצעות ניחוש ==== | ||
מנחשים את סוגו של אחד מהתושבים ומציבים במשוואות. אם מגיעים לסתירה אז יש להחליף את הסוג שנבחר ולפתור מחדש, אחרת נקבל מערכת משוואות פשוטה יותר. אם המערכת הזו עוד לא נותנת פתרון יחיד יש להמשיך לנחש עד לפתרון הסופי. אם החלפנו ניחוש ושוב הגענו לסתירה אז אין פתרון. | מנחשים את סוגו של אחד מהתושבים ומציבים במשוואות. אם מגיעים לסתירה אז יש להחליף את הסוג שנבחר ולפתור מחדש, אחרת נקבל מערכת משוואות פשוטה יותר. אם המערכת הזו עוד לא נותנת פתרון יחיד יש להמשיך לנחש עד לפתרון הסופי. אם החלפנו ניחוש ושוב הגענו לסתירה אז אין פתרון. | ||
| − | '''דוגמה 1.4:''' ננחש ש־<math>A</math> מ''דוגמה 1'' הוא אביר. מ־(2) נובע ש־<math>B</math> אביר ומ־(4) ש־<math>C</math> נוכל, אך זה סותר את (1) ולכן <math>A</math> נוכל. הצבה מחדש נותנת ש־<math>B</math> נוכל ו־<math>C,D</math> אבירים, וקיבלנו פתרון יחיד. | + | :'''דוגמה 1.4:''' ננחש ש־<math>A</math> מ''דוגמה 1'' הוא אביר. מ־(2) נובע ש־<math>B</math> אביר ומ־(4) ש־<math>C</math> נוכל, אך זה סותר את (1) ולכן <math>A</math> נוכל. הצבה מחדש נותנת ש־<math>B</math> נוכל ו־<math>C,D</math> אבירים, וקיבלנו פתרון יחיד. |
באופן כללי זו שיטה קלה יותר. אחד מהחסרונות שלה הוא שקשה למצוא באמצעותה את מספר הפתרונות, מה שעושים ע״י בדיקת היתכנות הסוג השני לכל תושב שניחשנו לו סוג. | באופן כללי זו שיטה קלה יותר. אחד מהחסרונות שלה הוא שקשה למצוא באמצעותה את מספר הפתרונות, מה שעושים ע״י בדיקת היתכנות הסוג השני לכל תושב שניחשנו לו סוג. | ||
| − | '''דוגמה 3:''' האורח נתקל בתושבים <math>A,B,C</math>, שאינם מרגלים. <math>A</math> טוען ש־<math>B</math> נוכל | + | :'''דוגמה 3:''' האורח נתקל בתושבים <math>A,B,C</math>, שאינם מרגלים. <math>A</math> טוען ש־<math>B</math> נוכל וגם <math>C</math> אביר, כלומר <math>A\leftrightarrow(\neg B\and C)=1</math>. אם ננחש ש־<math>A</math> אביר נקבל פתרון יחיד, אך אם ננחש שהוא נוכל נקבל ש־<math>\neg B\and C=0</math>. במקרה הזה אפשר לנחש ש־<math>B</math> נוכל (ולקבל פתרון יחיד) או אביר (ולקבל שני פתרונות). מספר הפתרונות הוא אם כן <math>\underbrace1_{A\text{ is a knight}}+\underbrace{\underbrace1_{B\text{ is a knave}}+\underbrace2_{B\text{ is a knight}}}_{A\text{ is a knave}}=4</math>. המערכת אינה לינארית ולכן אינה פתירה לפני משפט רושה–קפלי. |
חיסרון מהותי יותר הוא ששינוי של <math>\mathbf b</math> דורש פתרון מחדש של הבעיה כולה. <!---->כמו כן, הפתרון לא נותן לנו את התובנות שקיבלנו מפתרון כמערכת משוואות לינאריות, תובנות שיעזרו לנו בחידות שבהן שואלים שאלות. <!----> | חיסרון מהותי יותר הוא ששינוי של <math>\mathbf b</math> דורש פתרון מחדש של הבעיה כולה. <!---->כמו כן, הפתרון לא נותן לנו את התובנות שקיבלנו מפתרון כמערכת משוואות לינאריות, תובנות שיעזרו לנו בחידות שבהן שואלים שאלות. <!----> | ||
=== חידות עם שאלות === | === חידות עם שאלות === | ||
| − | נגדיר ''שאלה'' כפסוק לוגי שאנחנו יכולים לבחור ושתלוי בסוגים של | + | נגדיר ''שאלה'' כפסוק לוגי שאנחנו יכולים לבחור ושתלוי בסוגים של תושבים, כמו השאלה <math>X_1\or X_2</math>. נסמן כ־<math>n</math> את מספר התושבים ונניח שמותר לשאול עד <math>m</math> שאלות כדי להסיק את הסוג של כל אחד מהם. נסמן <math>\mathbf p=\begin{pmatrix}P_1\\\vdots\\P_m\end{pmatrix}</math> כווקטור השאלות. ''תשובה'' תוגדר כערך בוליאני השקול לוגית לשאלה ששאלנו, ונסמן ב־<math>\mathbf b=\begin{pmatrix}b_1\\\vdots\\b_m\end{pmatrix}</math> את וקטור התשובות. מההגדרות נובע ישירות ש־<math>\mathbf p=\mathbf b</math>. <math>\mathbf x</math> מוגדר כמקודם. |
| − | '''דוגמה 4:''' <math>m=n=2</math> ואין עובדות. וקטור השאלות <math>\mathbf p | + | :'''דוגמה 4:''' <math>m=n=2</math> ואין עובדות. וקטור השאלות <math>\mathbf p=\begin{pmatrix}X_1\leftrightarrow X_2\\X_1\end{pmatrix}</math> מאפשר לפתור את החידה. אם נניח, למשל, ש־<math>\mathbf b=\begin{pmatrix}0\\1\end{pmatrix}</math> אזי <math>\mathbf x=\begin{pmatrix}1\\0\end{pmatrix}</math>, ובאופן כללי <math>\mathbf x=\begin{pmatrix}b_2\\b_1\leftrightarrow b_2\end{pmatrix}</math>. |
<!-- | <!-- | ||
| − | |||
נוכיח שאם לא נתונות עובדות אז <math>n\le m</math>: החידה פתירה, כלומר קיים וקטור <math>\mathbf p</math> כנ״ל כך שלכל <math>\mathbf b</math> ניתן להסיק את הפתרון. מספר האפשרויות ל | נוכיח שאם לא נתונות עובדות אז <math>n\le m</math>: החידה פתירה, כלומר קיים וקטור <math>\mathbf p</math> כנ״ל כך שלכל <math>\mathbf b</math> ניתן להסיק את הפתרון. מספר האפשרויות ל | ||
| − | ושניתן להסתפק ב־<math>n</math> שאלות | + | ושניתן להסתפק ב־<math>n</math> שאלות |
במקרה שאין מרגלים ואין עובדות החידות האלה טריוויאליות – ניתן לשאול כל תושב "האם 1=1?" (או כל שאלה אחרת שהתשובה לה ידועה) ולהסיק את סוגו. זאת כמובן כאשר מספר השאלות שמותר לשאול הוא לכל הפחות מספר התושבים, מה שחייב להתקיים אם החידה פתירה: נניח שיש <math>n</math> תושבים ו־<math>m</math> שאלות וצ״ל ש־<math>n\le m</math>. לא נתונות עובדות על התושבים ולכן כל אחד מהם יכול להיות מכל סוג, כלומר יש <math>2^n</math> פתרונות אפשריים. | במקרה שאין מרגלים ואין עובדות החידות האלה טריוויאליות – ניתן לשאול כל תושב "האם 1=1?" (או כל שאלה אחרת שהתשובה לה ידועה) ולהסיק את סוגו. זאת כמובן כאשר מספר השאלות שמותר לשאול הוא לכל הפחות מספר התושבים, מה שחייב להתקיים אם החידה פתירה: נניח שיש <math>n</math> תושבים ו־<math>m</math> שאלות וצ״ל ש־<math>n\le m</math>. לא נתונות עובדות על התושבים ולכן כל אחד מהם יכול להיות מכל סוג, כלומר יש <math>2^n</math> פתרונות אפשריים. | ||
מספר הפתרונות האפשריים שווה גם ל־<math>2^n</math> ולכן <math>n=1=m</math>, כדרוש. עתה נניח ש־<math>n\le m</math> ל־<math>m,n</math> כלשהם ונוכיח שאם חידה עם <math>n+1</math> ו־ | מספר הפתרונות האפשריים שווה גם ל־<math>2^n</math> ולכן <math>n=1=m</math>, כדרוש. עתה נניח ש־<math>n\le m</math> ל־<math>m,n</math> כלשהם ונוכיח שאם חידה עם <math>n+1</math> ו־ | ||
| + | |||
| + | |||
| + | :'''דוגמה 5:''' <math>n=5,m=3</math> וידוע ש־<math>X_1\or X_2=1</math> ו־ | ||
--> | --> | ||
== חידות עם מרגלים == | == חידות עם מרגלים == | ||
| − | + | {| class="wikitable" style="direction:ltr; float:left; margin-top:0;" | |
| + | ! אופרטור !! ערך | ||
| + | |- | ||
| + | | <math>\neg X</math> || <math>1-X</math> | ||
| + | |- | ||
| + | | <math>X\and Y</math> || <math>XY</math> | ||
| + | |- | ||
| + | | <math>X\uparrow Y</math> || <math>1-XY</math> | ||
| + | |- | ||
| + | | <math>X\or Y</math> || <math>X+Y-XY</math> | ||
| + | |- | ||
| + | | <math>X\downarrow Y</math> || <math>1-X-Y+XY</math> | ||
| + | |- | ||
| + | | <math>X\rightarrow Y</math> || <math>1-X+XY</math> | ||
| + | |- | ||
| + | | <math>X\nrightarrow Y</math> || <math>X-XY</math> | ||
| + | |- | ||
| + | | <math>X\leftarrow Y</math> || <math>1-Y+XY</math> | ||
| + | |- | ||
| + | | <math>X\nleftarrow Y</math> || <math>Y-XY</math> | ||
| + | |- | ||
| + | | <math>X\leftrightarrow Y</math> || <math>1-X-Y+2XY</math> | ||
| + | |- | ||
| + | | <math>X\nleftrightarrow Y</math> || <math>X+Y-2XY</math> | ||
| + | |} | ||
| + | במקרה הזה נצטרך להכליל כמה הגדרות ולהגדיר כמה דברים חדשים. נרחיב את יחס השקילות <math>=</math> לתאר שיוויון של מספרים ממשיים בין 0 ל־1. אם תושב <math>X</math> מרגל נסמן <math>X=p</math> עבור קבוע <math>p\in(0,1)</math> כלשהו. האופרטורים <math>\neg,\and,\leftrightarrow,\dots</math> מוגדרים מחדש כמפורט בטבלה משמאל. לפי ההגדרות החדשות <math>X\and Y</math>, למשל, הוא ההסברות שהתושבים <math>X,Y</math> ידברו אמת בהנחה שהתושב <math>X</math> דובר אמת בהסברות <math>X</math> והתושב <math>Y</math> – בהסתברות <math>Y</math>. הגדרות אלה מכלילות את ההגדרות מאלגברה בוליאנית, אך יש כמה כללים שהאופרטורים כבר לא מקיימים. כללי דה־מורגן, למשל, נשמרים, בעוד שלא תמיד מתקיים <math>X\leftrightarrow Y=(X\rightarrow Y)\and(X\leftarrow Y)</math>. לבסוף, נגדיר אופרטור <math>\equiv</math> ע״י <math>X\equiv Y=\begin{cases}1,&X=Y\\0,&\text{else}\end{cases}</math> (בפרט, אם <math>X,Y</math> תושבים אז <math>X\equiv Y</math> הוא הערך הבוליאני שמציין אם הם מאותו סוג. אם <math>X,Y</math> אינם מרגלים אז <math>X\equiv Y=X\leftrightarrow Y</math>). | ||
| + | |||
| + | :'''דוגמה 6:''' האורח נתקל בתושבים <math>A,B,C</math>. אחד מהם אביר, אחד נוכל ואחד מרגל. <math>A</math> טוען ש־<math>C</math> נוכל, ו־<math>B</math> טוען ש־<math>A</math> שיקר הרגע. לכן מתקיים: | ||
| + | {{left|<math>\begin{array}{llcl} | ||
| + | (1)&A\leftrightarrow B\leftrightarrow C&=&1-p\\ | ||
| + | (2)&A\leftrightarrow(C\equiv0)&\neq&0\\ | ||
| + | (3)&B\leftrightarrow(C\not\equiv0)&\neq&0\end{array}</math>}} | ||
| + | :נעיר שמשוואה (1) לא רק נגררת מהעובדה שיש אביר, נוכל ומרגל, אלא שקולה לה. הוכחה: אגף ימין שלה אינו 0 או 1 ולכן לפחות אחד מ־<math>A,B,C</math> מרגל. נניח בלי הגבלת הכלליות ש־<math>A</math> מרגל ולכן <math>p\leftrightarrow B\leftrightarrow C=1-p-(B\leftrightarrow C)+2p(B\leftrightarrow C)=1-p</math>, ומכך נקבל <math>(B\leftrightarrow C)(1-2p)=0</math>. זה צריך להתקיים לכל <math>p\in(0,1)</math> ולכן <math>B\leftrightarrow C=0</math>, דהיינו <math>B+C-2BC=1</math>. חישוב באמצעות נגזרות יראה שלאגף שמאל יש נקודה קריטית אחת ב־<math>B=C=1/2</math>, ואז <math>B+C-2BC=1/2\ne1</math>. לכן היא מינימום והפתרון <math>(B,C)</math> נמצא על שפת <math>[0,1]^2</math>. נניח בלי הגבלת הכלליות ש־<math>B=0,1</math> ונקבל <math>C=1,0</math> בהתאמה, כלומר אכן יש אביר אחד, נוכל אחד ומרגל אחד. | ||
| + | |||
=== חידות ללא שאלות === | === חידות ללא שאלות === | ||
<!----> | <!----> | ||
| שורה 100: | שורה 134: | ||
* [https://en.wikipedia.org/wiki/Three-valued_logic Three-valued logic] | * [https://en.wikipedia.org/wiki/Three-valued_logic Three-valued logic] | ||
}} | }} | ||
| − | |||
<!-- סיבוכיות? --> | <!-- סיבוכיות? --> | ||
גרסה מ־21:02, 22 ביולי 2013
באי מסוים כל התושבים הם או אבירים, הדוברים תמיד אמת, או נוכלים, אשר תמיד משקרים. בחלק מהבעיות מוסיפים סוג נוסף – מרגלים, שעונים אמת או שקר באקראי. החידות דנות באורח באי המנסה להסיק מספר מסקנות – לרוב את הסוג של כמה מהתושבים – על סמך כמה עובדות (שמרביתן מהצורה "תושב 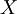 טען ש־
טען ש־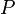 ") ו/או על סמך שאלות כן/לא שעליו לשאול.
") ו/או על סמך שאלות כן/לא שעליו לשאול.
- דוגמה 1: האורח נתקל בתושבים
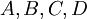 . אין מרגלים, וידוע ש־
. אין מרגלים, וידוע ש־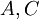 מסוגים שונים.
מסוגים שונים.  טוען ש־
טוען ש־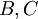 מאותו סוג,
מאותו סוג, 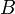 טוען ש־
טוען ש־ אביר ו־
אביר ו־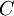 טוען שהוא מאותו סוג כמו
טוען שהוא מאותו סוג כמו 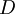 . מה הסוג של כל תושב?
. מה הסוג של כל תושב? - דוגמה 2: האורח נתקל בשלושה תושבים. אחד מהם אביר, אחד נוכל ואחד מרגל. אילו 3 שאלות של כן/לא הוא יכול לשאול על מנת לגלות את הסוג של כל אחד מהם, אם מותר לו להחליט למי להפנות כל שאלה על סמך התשובות לשאלות ששאל לפניה?
נרצה ליצור מודל מתמטי לפתרון בעיות מסוג זה.
תוכן עניינים
חידות ללא מרגלים
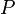 |
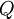 |

|
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
באלגברה בוליאנית מסמנים 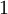 כפסוק אמת ו־
כפסוק אמת ו־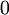 כפסוק שקר. נעזר בסימון
כפסוק שקר. נעזר בסימון 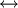 לציון אופרטור שקילות לוגית, המוגדר כמפורט בטבלה שמשמאל.
לציון אופרטור שקילות לוגית, המוגדר כמפורט בטבלה שמשמאל.  הוא יחס שקילות בין כל שני פסוקים שקולים לוגית, כלומר אם ידוע ש־
הוא יחס שקילות בין כל שני פסוקים שקולים לוגית, כלומר אם ידוע ש־ נותן 1 אז נוכל לסמן
נותן 1 אז נוכל לסמן 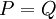 . אם תושב
. אם תושב 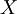 הוא אביר אז נסמן
הוא אביר אז נסמן 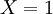 ואם נוכל –
ואם נוכל – 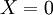 . לפיכך, אם
. לפיכך, אם 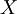 טוען טענה
טוען טענה 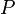 אז
אז 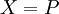 .
.
- דוגמה 1.1: באמצעות סימונים אלו נציג את דוגמה 1 כמערכת משוואות בוליאניות.
 טוען ש־
טוען ש־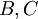 מאותו סוג, כלומר הוא טוען
מאותו סוג, כלומר הוא טוען 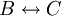 . מכך נובעת משוואה (1) במערכת המשוואות הבאה. מהטענות של
. מכך נובעת משוואה (1) במערכת המשוואות הבאה. מהטענות של 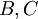 נובעות המשוואות (2) ו־(3), ומהעובדה ש־
נובעות המשוואות (2) ו־(3), ומהעובדה ש־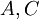 שונים נובעת משוואה (4):
שונים נובעת משוואה (4):
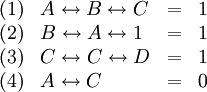
- באופן שקול:
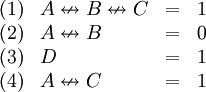
- כאשר
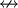 מציין אופרטור XOR, המסומן גם כ־
מציין אופרטור XOR, המסומן גם כ־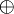 .
.
בסימונים אלו נגדיר עובדה בתור משוואה בוליאנית שנתונה בחידה, כגון 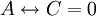 מדוגמה 1.
מדוגמה 1.
חידות ללא שאלות
פתרון כמערכת משוואות
ברגע שיש לנו ניסוח מתמטי של החידה כמערכת משוואות אפשר לפתור אותה. אנו נתעמק בחידות שניתן לפתור כמערכת משוואות לינאריות כיוון שהן נותנות מידע רב יותר על החידה, כפי שנראה בהמשך.
ניצור איזומורפיזם מהשדה 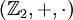 ל־
ל־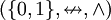 ע״י
ע״י ![x\mapsto\begin{cases}0,&x=[0]_2\\1,&x=[1]_2\end{cases}](/images/math/9/8/6/98672584359ace20c51bd753cd9e6e05.png) . מכך נובע ש־
. מכך נובע ש־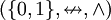 שדה. סכום
שדה. סכום 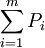 (כאשר
(כאשר 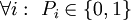 ) יוגדר בתור
) יוגדר בתור 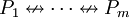 ומכפלה
ומכפלה 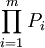 בתור
בתור 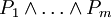 . גם כפל מטריצות מוגדר בהתאם.
. גם כפל מטריצות מוגדר בהתאם.
כעת, אם התושבים הם 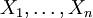 אז נסמן
אז נסמן 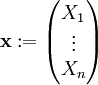 . אם כל
. אם כל 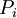 מייצג נעלם
מייצג נעלם 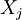 או קבוע
או קבוע 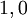 אז נוכל להציג כל
אז נוכל להציג כל 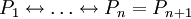 בתור סכום של נעלמים שונים השווה לקבוע: לדוגמה,
בתור סכום של נעלמים שונים השווה לקבוע: לדוגמה, 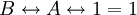 מהניסוח המתמטי של דוגמה 1 שקול ל־
מהניסוח המתמטי של דוגמה 1 שקול ל־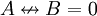 , כלומר ל־
, כלומר ל־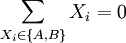 . לכן נוכל להגדיר מטריצת מקדמים
. לכן נוכל להגדיר מטריצת מקדמים 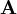 ווקטור מקדמים חופשיים
ווקטור מקדמים חופשיים 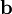 כך ש־
כך ש־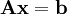 .
.
- דוגמה 1.2: ההצגה המטריציונית של דוגמה 1 היא
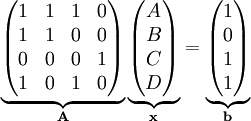
הצגה זו מאפשרת לנו למצוא מה הסוג של כל תושב ע״י פתרון מערכת משוואות לינאריות. יתרה מזאת, לפי משפט רושה–קפלי (Rouché–Capelli) יש פתרון ל־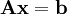 אם״ם
אם״ם 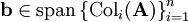 כאשר
כאשר 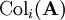 העמודה ה־
העמודה ה־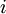 של
של 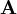 , ואם כן אז מרחב הפתרונות הוא ממימד
, ואם כן אז מרחב הפתרונות הוא ממימד 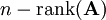 . מכאן נובע שאנו יכולים לבדוק האם קיים פתרון לחידה, ואם כן לחשב את מספר הפתרונות בתור
. מכאן נובע שאנו יכולים לבדוק האם קיים פתרון לחידה, ואם כן לחשב את מספר הפתרונות בתור 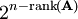 . מובן שבד״כ יש רק פתרון אחד, כלומר
. מובן שבד״כ יש רק פתרון אחד, כלומר 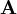 הפיכה.
הפיכה.
- דוגמה 1.3: נפתור את דוגמה 1. חישוב פשוט מראה ש־
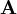 הפיכה (ומכאן שיש פתרון יחיד) ו־
הפיכה (ומכאן שיש פתרון יחיד) ו־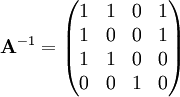 . לכן
. לכן 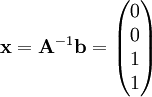 – התושבים
– התושבים 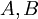 נוכלים ו־
נוכלים ו־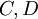 אבירים.
אבירים.
פתרון באמצעות ניחוש
מנחשים את סוגו של אחד מהתושבים ומציבים במשוואות. אם מגיעים לסתירה אז יש להחליף את הסוג שנבחר ולפתור מחדש, אחרת נקבל מערכת משוואות פשוטה יותר. אם המערכת הזו עוד לא נותנת פתרון יחיד יש להמשיך לנחש עד לפתרון הסופי. אם החלפנו ניחוש ושוב הגענו לסתירה אז אין פתרון.
- דוגמה 1.4: ננחש ש־
 מדוגמה 1 הוא אביר. מ־(2) נובע ש־
מדוגמה 1 הוא אביר. מ־(2) נובע ש־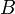 אביר ומ־(4) ש־
אביר ומ־(4) ש־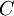 נוכל, אך זה סותר את (1) ולכן
נוכל, אך זה סותר את (1) ולכן  נוכל. הצבה מחדש נותנת ש־
נוכל. הצבה מחדש נותנת ש־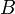 נוכל ו־
נוכל ו־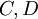 אבירים, וקיבלנו פתרון יחיד.
אבירים, וקיבלנו פתרון יחיד.
באופן כללי זו שיטה קלה יותר. אחד מהחסרונות שלה הוא שקשה למצוא באמצעותה את מספר הפתרונות, מה שעושים ע״י בדיקת היתכנות הסוג השני לכל תושב שניחשנו לו סוג.
- דוגמה 3: האורח נתקל בתושבים
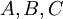 , שאינם מרגלים.
, שאינם מרגלים.  טוען ש־
טוען ש־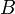 נוכל וגם
נוכל וגם 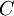 אביר, כלומר
אביר, כלומר 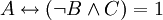 . אם ננחש ש־
. אם ננחש ש־ אביר נקבל פתרון יחיד, אך אם ננחש שהוא נוכל נקבל ש־
אביר נקבל פתרון יחיד, אך אם ננחש שהוא נוכל נקבל ש־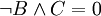 . במקרה הזה אפשר לנחש ש־
. במקרה הזה אפשר לנחש ש־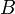 נוכל (ולקבל פתרון יחיד) או אביר (ולקבל שני פתרונות). מספר הפתרונות הוא אם כן
נוכל (ולקבל פתרון יחיד) או אביר (ולקבל שני פתרונות). מספר הפתרונות הוא אם כן 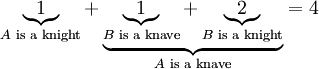 . המערכת אינה לינארית ולכן אינה פתירה לפני משפט רושה–קפלי.
. המערכת אינה לינארית ולכן אינה פתירה לפני משפט רושה–קפלי.
חיסרון מהותי יותר הוא ששינוי של 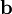 דורש פתרון מחדש של הבעיה כולה. כמו כן, הפתרון לא נותן לנו את התובנות שקיבלנו מפתרון כמערכת משוואות לינאריות, תובנות שיעזרו לנו בחידות שבהן שואלים שאלות.
דורש פתרון מחדש של הבעיה כולה. כמו כן, הפתרון לא נותן לנו את התובנות שקיבלנו מפתרון כמערכת משוואות לינאריות, תובנות שיעזרו לנו בחידות שבהן שואלים שאלות.
חידות עם שאלות
נגדיר שאלה כפסוק לוגי שאנחנו יכולים לבחור ושתלוי בסוגים של תושבים, כמו השאלה 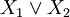 . נסמן כ־
. נסמן כ־ את מספר התושבים ונניח שמותר לשאול עד
את מספר התושבים ונניח שמותר לשאול עד 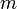 שאלות כדי להסיק את הסוג של כל אחד מהם. נסמן
שאלות כדי להסיק את הסוג של כל אחד מהם. נסמן 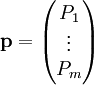 כווקטור השאלות. תשובה תוגדר כערך בוליאני השקול לוגית לשאלה ששאלנו, ונסמן ב־
כווקטור השאלות. תשובה תוגדר כערך בוליאני השקול לוגית לשאלה ששאלנו, ונסמן ב־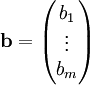 את וקטור התשובות. מההגדרות נובע ישירות ש־
את וקטור התשובות. מההגדרות נובע ישירות ש־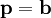 .
. 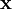 מוגדר כמקודם.
מוגדר כמקודם.
- דוגמה 4:
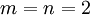 ואין עובדות. וקטור השאלות
ואין עובדות. וקטור השאלות 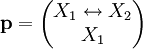 מאפשר לפתור את החידה. אם נניח, למשל, ש־
מאפשר לפתור את החידה. אם נניח, למשל, ש־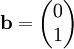 אזי
אזי 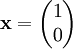 , ובאופן כללי
, ובאופן כללי 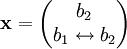 .
.
חידות עם מרגלים
| אופרטור | ערך |
|---|---|
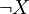 |
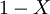
|
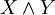 |
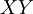
|
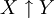 |
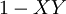
|
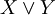 |
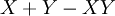
|
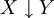 |
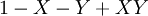
|
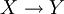 |
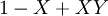
|
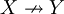 |
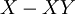
|
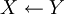 |
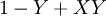
|
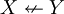 |
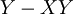
|
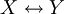 |
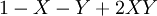
|
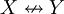 |
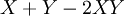
|
במקרה הזה נצטרך להכליל כמה הגדרות ולהגדיר כמה דברים חדשים. נרחיב את יחס השקילות  לתאר שיוויון של מספרים ממשיים בין 0 ל־1. אם תושב
לתאר שיוויון של מספרים ממשיים בין 0 ל־1. אם תושב 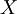 מרגל נסמן
מרגל נסמן 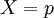 עבור קבוע
עבור קבוע 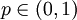 כלשהו. האופרטורים
כלשהו. האופרטורים 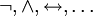 מוגדרים מחדש כמפורט בטבלה משמאל. לפי ההגדרות החדשות
מוגדרים מחדש כמפורט בטבלה משמאל. לפי ההגדרות החדשות 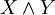 , למשל, הוא ההסברות שהתושבים
, למשל, הוא ההסברות שהתושבים 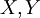 ידברו אמת בהנחה שהתושב
ידברו אמת בהנחה שהתושב 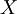 דובר אמת בהסברות
דובר אמת בהסברות 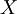 והתושב
והתושב 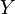 – בהסתברות
– בהסתברות 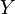 . הגדרות אלה מכלילות את ההגדרות מאלגברה בוליאנית, אך יש כמה כללים שהאופרטורים כבר לא מקיימים. כללי דה־מורגן, למשל, נשמרים, בעוד שלא תמיד מתקיים
. הגדרות אלה מכלילות את ההגדרות מאלגברה בוליאנית, אך יש כמה כללים שהאופרטורים כבר לא מקיימים. כללי דה־מורגן, למשל, נשמרים, בעוד שלא תמיד מתקיים  . לבסוף, נגדיר אופרטור
. לבסוף, נגדיר אופרטור  ע״י
ע״י 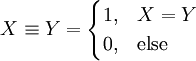 (בפרט, אם
(בפרט, אם 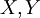 תושבים אז
תושבים אז 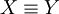 הוא הערך הבוליאני שמציין אם הם מאותו סוג. אם
הוא הערך הבוליאני שמציין אם הם מאותו סוג. אם 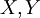 אינם מרגלים אז
אינם מרגלים אז 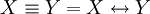 ).
).
- דוגמה 6: האורח נתקל בתושבים
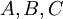 . אחד מהם אביר, אחד נוכל ואחד מרגל.
. אחד מהם אביר, אחד נוכל ואחד מרגל.  טוען ש־
טוען ש־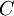 נוכל, ו־
נוכל, ו־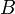 טוען ש־
טוען ש־ שיקר הרגע. לכן מתקיים:
שיקר הרגע. לכן מתקיים:
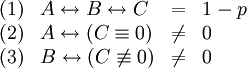
- נעיר שמשוואה (1) לא רק נגררת מהעובדה שיש אביר, נוכל ומרגל, אלא שקולה לה. הוכחה: אגף ימין שלה אינו 0 או 1 ולכן לפחות אחד מ־
 מרגל. נניח בלי הגבלת הכלליות ש־
מרגל. נניח בלי הגבלת הכלליות ש־ מרגל ולכן
מרגל ולכן 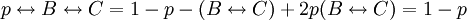 , ומכך נקבל
, ומכך נקבל 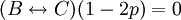 . זה צריך להתקיים לכל
. זה צריך להתקיים לכל 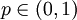 ולכן
ולכן 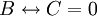 , דהיינו
, דהיינו 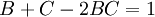 . חישוב באמצעות נגזרות יראה שלאגף שמאל יש נקודה קריטית אחת ב־
. חישוב באמצעות נגזרות יראה שלאגף שמאל יש נקודה קריטית אחת ב־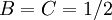 , ואז
, ואז 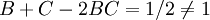 . לכן היא מינימום והפתרון
. לכן היא מינימום והפתרון 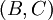 נמצא על שפת
נמצא על שפת ![[0,1]^2](/images/math/5/1/4/514392e7ca5fed0c25ab1ea0b6b6b045.png) . נניח בלי הגבלת הכלליות ש־
. נניח בלי הגבלת הכלליות ש־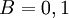 ונקבל
ונקבל 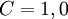 בהתאמה, כלומר אכן יש אביר אחד, נוכל אחד ומרגל אחד.
בהתאמה, כלומר אכן יש אביר אחד, נוכל אחד ומרגל אחד.