הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/1.5.11"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
מ (←‏דוגמאות)
מ (←‏אינטגרל לא אמיתי, סוג II)
שורה 20: שורה 20:
 
# <math>\int\limits_0^\frac12\frac{\mathrm dx}{x(\ln(x))^2}</math>. נציב <math>y=\ln(x)</math> וכן <math>\mathrm dy=\frac{\mathrm dx}x</math> לקבל <math>\lim_{R\to0^+}\int\limits_{\ln(R)}^{\ln\left(\frac12\right)}\frac{\mathrm dy}{y^2}=\lim_{R\to0^+}-\frac1{\ln(1/2)}+\frac1{\ln(R)}=-\frac1{\ln(1/2)}</math> כלומר מתכנס.
 
# <math>\int\limits_0^\frac12\frac{\mathrm dx}{x(\ln(x))^2}</math>. נציב <math>y=\ln(x)</math> וכן <math>\mathrm dy=\frac{\mathrm dx}x</math> לקבל <math>\lim_{R\to0^+}\int\limits_{\ln(R)}^{\ln\left(\frac12\right)}\frac{\mathrm dy}{y^2}=\lim_{R\to0^+}-\frac1{\ln(1/2)}+\frac1{\ln(R)}=-\frac1{\ln(1/2)}</math> כלומר מתכנס.
 
# דרך כתיבה מקוצרת: <math>\int\limits_0^1\frac{\mathrm dx}\sqrt x=\int\limits_0^1 x^{-\frac12}\mathrm dx=\left[\frac{x^{1/2}}{1/2}\right]_{x=0}^1=2</math>.
 
# דרך כתיבה מקוצרת: <math>\int\limits_0^1\frac{\mathrm dx}\sqrt x=\int\limits_0^1 x^{-\frac12}\mathrm dx=\left[\frac{x^{1/2}}{1/2}\right]_{x=0}^1=2</math>.
 +
  
 
----
 
----
 +
  
 
לגבי משפטי התכנסות יש אנלוגיות למשפטים שהוכחנו עבור אינטגרל לא אמיתי מסוג ראשון. נרשום אותם ללא הוכחה.
 
לגבי משפטי התכנסות יש אנלוגיות למשפטים שהוכחנו עבור אינטגרל לא אמיתי מסוג ראשון. נרשום אותם ללא הוכחה.
שורה 32: שורה 34:
 
==משפט 3==
 
==משפט 3==
 
תהי f מוגדרת ומונוטונית בקטע <math>(a,b]</math> אזי <math>\lim_{x\to a^+} f(x)</math> קיים אם"ם f חסומה בקטע <math>(a,b]</math>.
 
תהי f מוגדרת ומונוטונית בקטע <math>(a,b]</math> אזי <math>\lim_{x\to a^+} f(x)</math> קיים אם"ם f חסומה בקטע <math>(a,b]</math>.
−
===מסקנה===
+
 
 +
==משפט 4==
 
עבור f אינטגרבילית מקומית ב-<math>(a,b]</math> כך ש-<math>f(x)\ge0</math> האינטגרל <math>\int\limits_a^b f</math> מתכנס אם"ם האינטגרלים החלקיים <math>\int\limits_c^b f</math> חסומים כאשר <math>c\to a^+</math>.
 
עבור f אינטגרבילית מקומית ב-<math>(a,b]</math> כך ש-<math>f(x)\ge0</math> האינטגרל <math>\int\limits_a^b f</math> מתכנס אם"ם האינטגרלים החלקיים <math>\int\limits_c^b f</math> חסומים כאשר <math>c\to a^+</math>.
−
==משפט 4 {{הערה|(מבחן ההשוואה)}}==
+
 
 +
==משפט 5 {{הערה|(מבחן ההשוואה)}}==
 
נניח שב-<math>(a,b]</math> הפונקציות f,g אינטגרביליות מקומית וכן <math>0\le f(x)\le g(x)</math>.
 
נניח שב-<math>(a,b]</math> הפונקציות f,g אינטגרביליות מקומית וכן <math>0\le f(x)\le g(x)</math>.
 
* אם <math>\int\limits_a^b g</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס.
 
* אם <math>\int\limits_a^b g</math> מתכנס אז <math>\int\limits_a^b f</math> מתכנס.
 
* אם <math>\int\limits_a^b f</math> מתבדר אז <math>\int\limits_a^b g</math> מתבדר.
 
* אם <math>\int\limits_a^b f</math> מתבדר אז <math>\int\limits_a^b g</math> מתבדר.

גרסה מ־14:01, 5 במאי 2011

את משפט 10 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-1.5.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.

אינטגרל לא אמיתי, סוג I (המשך)

תזכורת: עד כאן דיברנו רק על אינטגרלים מהסוג 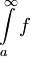\int\limits_a^\infty f. כמובן שיש מקבילית גמורה לאינטגרלים האלה: 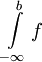\int\limits_{-\infty}^b f. כמובן שאפשר לתרגם את כל המשפטים שלנו למקרה זה.

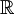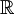הגדרה: תהי f מוגדרת בכל \mathbb R. נאמר שהיא אינטגרבילית מקומית אם היא אינטגרבילית בכל קטע סופי [a,b]. למשל, אם f רציפה למקוטעין ב-\mathbb R אז היא אינטגרבילית מקומית.

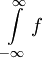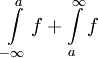תזכורת: תהי f מוגדרת ואינטגרבילית מקומית. הגדרנו \int\limits_{-\infty}^\infty f להיות \int\limits_{-\infty}^a f+\int\limits_a^\infty f בתנאי ששני האינטגרלים התכנסים. אם אפילו אחד מהם מתבדר נאמר ש-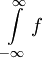\int\limits_{-\infty}^\infty f מתבדר. נבדוק שההגדרה בלתי תלוייה ב-a. ובכן בה"כ נבחר 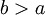b>a ונבדוק את שתי הטענות הבאות:

  • שני האינטגרלים 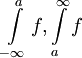\int\limits_{-\infty}^a f,\int\limits_a^\infty f מתכנסים אם"ם שני האינטגרלים 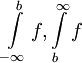\int\limits_{-\infty}^b f,\int\limits_b^\infty f מתכנסים.
    עפ"י משפט 2 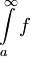\int\limits_a^\infty f מתכנס אם"ם 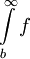\int\limits_b^\infty f מתכנס. באותו אופן 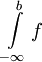\int\limits_{-\infty}^b f מתכנס אם"ם 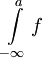\int\limits_{-\infty}^a f מתכנס, לכן הטענה מתקיימת.
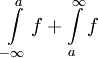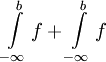  • נוכיח שבמקרה שהאינטגרלים מתכנסים \int\limits_{-\infty}^a f+\int\limits_a^\infty f אז הם שווים ל-\int\limits_{-\infty}^b f+\int\limits_{-\infty}^b f.
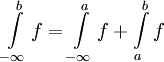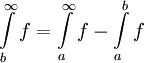    ובכן עפ"י משפט 2 \int\limits_{-\infty}^b f=\int\limits_{-\infty}^a f+\int\limits_a^b f וגם \int\limits_b^\infty f=\int\limits_a^\infty f-\int\limits_a^b f. נחבר את התוצאות ונקבל את הטענה.

אינטגרל לא אמיתי, סוג II

מדובר באינטגרל על קטע סגור של פונקציה לא חסומה.

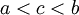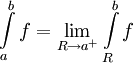הגדרה: תהי f מוגדרת בקטע (a,b]. נאמר ש-f אינטגרבילית מקומית בקטע זה אם לכל c כך ש-a<c<b f אינטגרבילית בקטע [c,b] (למשל, אם f רציפה למקוטעין ב-(a,b]). לכן נגדיר \int\limits_a^b f=\lim_{R\to a^+}\int\limits_R^b f אם הגבול קיים. אם כן אומרים שהאינטגרל \int\limits_a^b f מתכנס או ש-f אינטגרבילית בקטע (a,b]. אם אין גבול אומרים ש-\int\limits_a^b f מתבדר.

דוגמאות

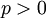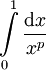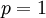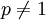  1. נקח p>0 ונתבונן באינטגרל הלא אמיתי \int\limits_0^1\frac{\mathrm dx}{x^p}. עבור p=1 נקבל \lim_{R\to0^+}\int\limits_R^1\frac{\mathrm dx}x=\lim_{R\to0^+}[\ln|x|]_{x=R}^1=\lim_{R\to0^+}-\ln(R)=\infty והאינטגרל מתבדר. עבור p\ne1 נקבל \lim_{R\to0^+}\int\limits_R^1\frac{\mathrm dx}{x^p}=\lim_{R\to0^+}\left[\frac{x^{-p+1}}{-p+1}\right]_{x=R}^1=\lim_{R\to0^+}\frac1{1-p}-\frac{R^{-p+1}}{-p+1}=\begin{cases}\frac1{1-p}&p<1\\\infty&\text{else}\end{cases}.
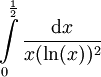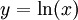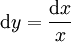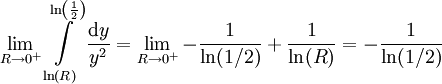  2. \int\limits_0^\frac12\frac{\mathrm dx}{x(\ln(x))^2}. נציב y=\ln(x) וכן \mathrm dy=\frac{\mathrm dx}x לקבל \lim_{R\to0^+}\int\limits_{\ln(R)}^{\ln\left(\frac12\right)}\frac{\mathrm dy}{y^2}=\lim_{R\to0^+}-\frac1{\ln(1/2)}+\frac1{\ln(R)}=-\frac1{\ln(1/2)} כלומר מתכנס.
  3. דרך כתיבה מקוצרת: \int\limits_0^1\frac{\mathrm dx}\sqrt x=\int\limits_0^1 x^{-\frac12}\mathrm dx=\left[\frac{x^{1/2}}{1/2}\right]_{x=0}^1=2.



לגבי משפטי התכנסות יש אנלוגיות למשפטים שהוכחנו עבור אינטגרל לא אמיתי מסוג ראשון. נרשום אותם ללא הוכחה.

משפט 1

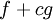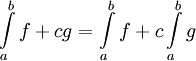אם f ו-g אינטגרביליות ב-(a,b] ואם c קבוע אז f+cg אינטגרבילית בקטע (a,b] ומתקיים \int\limits_a^bf+cg=\int\limits_a^b f+c\int\limits_a^b g.

משפט 2

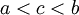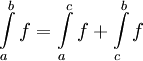נניח ש-a<c<b ו-f אינטגרבילית מקומית ב-(a,b]. אזי f אינטגרבילית בקטע (a,b] אם"ם היא אינטגרבילית בקטע (a,c] ואם כן \int\limits_a^b f=\int\limits_a^c f+\int\limits_c^b f.

משפט 3

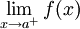תהי f מוגדרת ומונוטונית בקטע (a,b] אזי \lim_{x\to a^+} f(x) קיים אם"ם f חסומה בקטע (a,b].

משפט 4

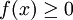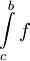עבור f אינטגרבילית מקומית ב-(a,b] כך ש-f(x)\ge0 האינטגרל \int\limits_a^b f מתכנס אם"ם האינטגרלים החלקיים \int\limits_c^b f חסומים כאשר c\to a^+.

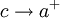משפט 5 (מבחן ההשוואה)

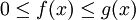נניח שב-(a,b] הפונקציות f,g אינטגרביליות מקומית וכן 0\le f(x)\le g(x).

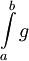  • אם \int\limits_a^b g מתכנס אז \int\limits_a^b f מתכנס.
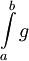  • אם \int\limits_a^b f מתבדר אז \int\limits_a^b g מתבדר.
מקור: https://math-wiki.com/index.php?title=משתמש:אור_שחף/133_-_הרצאה/1.5.11&oldid=10465