הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/12.4.11"
(←הוכחה) |
|||
| שורה 2: | שורה 2: | ||
=אינטגרל לא אמיתי, סוג I {{הערה|(המשך)}}= | =אינטגרל לא אמיתי, סוג I {{הערה|(המשך)}}= | ||
| − | '''הגדרה:''' תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. נאמר ש-<math>\int\limits_a^\infty f</math> מתכנס בהחלט אם <math>\int\limits_a^\infty|f|</math> מתכנס. אם האינטגרל מתכנס לא בהחלט נאמר שהוא מתכנס בתנאי. | + | '''הגדרה:''' תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. נאמר ש-<math>\int\limits_a^\infty f</math> מתכנס בהחלט אם <math>\int\limits_a^\infty|f|</math> מתכנס. אם האינטגרל מתכנס אבל לא בהחלט נאמר שהוא מתכנס בתנאי. |
==משפט 8== | ==משפט 8== | ||
תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. אם <math>\int\limits_a^\infty|f|</math> מתכנס אז <math>\int\limits_a^\infty f</math> מתכנס. במילים: אם f אינטגרבילית בהחלט בקטע <math>[a,\infty)</math> אז f אינטגרבילית בקטע. | תהי f מוגדרת ואינטגרבילית מקומית ב-<math>[a,\infty)</math>. אם <math>\int\limits_a^\infty|f|</math> מתכנס אז <math>\int\limits_a^\infty f</math> מתכנס. במילים: אם f אינטגרבילית בהחלט בקטע <math>[a,\infty)</math> אז f אינטגרבילית בקטע. | ||
| שורה 10: | שורה 10: | ||
''גישה אחרת:'' נגדיר <math>f^+(x)=\begin{cases}f(x)&f(x)\ge0\\0&\text{else}\end{cases}</math> וכן <math>f^-(x)=\begin{cases}0&f(x)>0\\-f(x)&\text{else}\end{cases}</math>. לכן <math>f^+(x),f^-(x)</math> אי-שליליות. קל להראות שלכל x, <math>f(x)=f^+(x)-f^-(x)</math> וכן <math>|f(x)|=f^+(x)+f^-(x)</math> (גאומטרית: <math>\int\limits_a^b f^+</math> השטח שמעל ציר ה-x ו-<math>\int\limits_a^b f^-</math> השטח שמתחת). | ''גישה אחרת:'' נגדיר <math>f^+(x)=\begin{cases}f(x)&f(x)\ge0\\0&\text{else}\end{cases}</math> וכן <math>f^-(x)=\begin{cases}0&f(x)>0\\-f(x)&\text{else}\end{cases}</math>. לכן <math>f^+(x),f^-(x)</math> אי-שליליות. קל להראות שלכל x, <math>f(x)=f^+(x)-f^-(x)</math> וכן <math>|f(x)|=f^+(x)+f^-(x)</math> (גאומטרית: <math>\int\limits_a^b f^+</math> השטח שמעל ציר ה-x ו-<math>\int\limits_a^b f^-</math> השטח שמתחת). | ||
| − | כעת אם נתון ש-<math>\int\limits_a^\infty|f|</math> מתכנס, מבחן ההשוואה אומר שכיוון ש-<math>0\le f^+(x),f^-(x)\le|f(x)|</math> שני האינטגרלים <math>\int\limits_a^\infty f^+,\int\limits_a^\infty f^-</math> מתכנסים ונובע ממשפט 1 ש-<math>\int\limits_a^\infty f=\int\limits_a^\infty(f^+-f^-)=\int\limits_a^\infty f^+-\int\limits_a^\infty f^-\in\mathbb R</math>, כלומר <math>\int\limits_a^\infty f</math> מתכנס. {{משל}} | + | כעת, אם נתון ש-<math>\int\limits_a^\infty|f|</math> מתכנס, מבחן ההשוואה אומר שכיוון ש-<math>0\le f^+(x),f^-(x)\le|f(x)|</math> שני האינטגרלים <math>\int\limits_a^\infty f^+,\int\limits_a^\infty f^-</math> מתכנסים ונובע ממשפט 1 ש-<math>\int\limits_a^\infty f=\int\limits_a^\infty(f^+-f^-)=\int\limits_a^\infty f^+-\int\limits_a^\infty f^-\in\mathbb R</math>, כלומר <math>\int\limits_a^\infty f</math> מתכנס. {{משל}} |
==דוגמאות== | ==דוגמאות== | ||
| − | * <math>\int\limits_2^\infty\frac{\sin(x)}{x^2}\mathrm dx</math> - מתכנס או מתבדר? נראה התכנסות ע"י הוכחת התכנסות בהחלט: <math>0\le\left|\frac{\sin(x)}{x^2}\right|\le\frac1{x^2}</math> ולכן, עפ"י מבחן ההשוואה, <math>\int\limits_2^\infty\left|\frac{\sin(x)}{x^2}\right|\mathrm dx</math> מתכנס. {{משל}} | + | * <math>\int\limits_2^\infty\frac{\sin(x)}{x^2}\mathrm dx</math> - מתכנס או מתבדר? נראה התכנסות ע"י הוכחת התכנסות בהחלט: <math>0\le\left|\frac{\sin(x)}{x^2}\right|\le\frac1{x^2}</math> ולכן, עפ"י מבחן ההשוואה עם <math>\int\limits_2^\infty\frac{\mathrm dx}{x^2}</math>, <math>\int\limits_2^\infty\left|\frac{\sin(x)}{x^2}\right|\mathrm dx</math> מתכנס. {{משל}} |
| − | * נבנה דוגמאות של f מוגדרת ורציפה ב-<math>[0,\infty)</math> כך ש-<math>\int\limits_0^\infty f</math> מתכנס אעפ"י ש-<math>\sum_{n=0}^\infty f(n)</math>, ולהיפך: <math>\sum_{n=0}^\infty f(n)</math> מתכנס ואילו <math>\int\limits_0^\infty f</math> מתבדר. ובכן אם <math>f(x)=\sin(\pi x)</math> אז <math>\int\limits_0^\infty f=\lim_{R\to\infty}\int\limits_0^R\sin(\pi x)\mathrm dx=\lim_{R\to\infty}\left[\frac{-\cos(\pi x)}\pi\right]_{x=0}^R</math> ואין גבול, לכן האינטגרל מתבדר. לעומת זאת, <math>\sum_{n=0}^\infty\sin(\pi n)=\sum_{n=0}^\infty 0=0</math>, שבוודאי מתכנס. לצד השני נגדיר פונקציה f ע"י הגרף [[קובץ:גרף פונקציית משולשים 2.png|600px]]<br />אזי <math>\sum_{n=0}^\infty f(n)=\sum_{n=0}^\infty 1=\infty</math> - מתבדר. לעומת זאת, {{left|<math>\int\limits_0^\infty f=</math> השטח שמתחת לגרף <math>=\frac12\cdot\frac12+\lim_{n\to\infty}\frac12\left(\frac12+\frac14+\frac18+\dots+\frac1{2^n}\right)=\frac14+\frac12=\frac34</math>}}{{משל}} | + | * נבנה דוגמאות של f מוגדרת ורציפה ב-<math>[0,\infty)</math> כך ש-<math>\int\limits_0^\infty f</math> מתכנס אעפ"י ש-<math>\sum_{n=0}^\infty f(n)</math> מתבדר, ולהיפך: <math>\sum_{n=0}^\infty f(n)</math> מתכנס ואילו <math>\int\limits_0^\infty f</math> מתבדר. ובכן, אם <math>f(x)=\sin(\pi x)</math> אז <math>\int\limits_0^\infty f=\lim_{R\to\infty}\int\limits_0^R\sin(\pi x)\mathrm dx=\lim_{R\to\infty}\left[\frac{-\cos(\pi x)}\pi\right]_{x=0}^R</math> ואין גבול, לכן האינטגרל מתבדר. לעומת זאת, <math>\sum_{n=0}^\infty\sin(\pi n)=\sum_{n=0}^\infty 0=0</math>, שבוודאי מתכנס. לצד השני נגדיר פונקציה f ע"י הגרף [[קובץ:גרף פונקציית משולשים 2.png|600px]]<br />אזי <math>\sum_{n=0}^\infty f(n)=\sum_{n=0}^\infty 1=\infty</math> - מתבדר. לעומת זאת, {{left|<math>\int\limits_0^\infty f=</math> השטח שמתחת לגרף <math>=\frac12\cdot\frac12+\lim_{n\to\infty}\frac12\left(\frac12+\frac14+\frac18+\dots+\frac1{2^n}\right)=\frac14+\frac12=\frac34</math>}}{{משל}} |
==משפט 9 {{הערה|(מבחן דיריכלה)}}== | ==משפט 9 {{הערה|(מבחן דיריכלה)}}== | ||
נניח ש-f מוגדרת ורציפה ב-<math>[a,\infty)</math> ונניח שהאינטגרלים החלקיים <math>\int\limits_a^b f</math> חסומים כאשר <math>b\to\infty</math> (ז"א קיים <math>M\ge0</math> כך ש-<math>\forall b>a:\ \left|\int\limits_a^b f\right|\le M</math>). עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב-<math>[a,\infty)</math> ו-<math>\lim_{x\to\infty} g(x)=0</math> אזי <math>\int\limits_a^\infty f(x)g(x)\mathrm dx</math> מתכנס. | נניח ש-f מוגדרת ורציפה ב-<math>[a,\infty)</math> ונניח שהאינטגרלים החלקיים <math>\int\limits_a^b f</math> חסומים כאשר <math>b\to\infty</math> (ז"א קיים <math>M\ge0</math> כך ש-<math>\forall b>a:\ \left|\int\limits_a^b f\right|\le M</math>). עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב-<math>[a,\infty)</math> ו-<math>\lim_{x\to\infty} g(x)=0</math> אזי <math>\int\limits_a^\infty f(x)g(x)\mathrm dx</math> מתכנס. | ||
===הוכחה=== | ===הוכחה=== | ||
| − | לכל <math>x>a</math> נגדיר <math>F(x)=\int\limits_a^x f</math>. כיוון ש-f רציפה המשפט היסודי אומר ש-<math>F'(x)=f(x)</math> לכל <math>x>a</math>. יתר על כן, הנתונים שלנו גוררים ש-<math>\forall x>a:\ |F(x)|\le M</math>. כעת <math>\int\limits_a^\infty f\cdot g=\left[F(x)g(x)\right]_{x=a}^\infty-\int\limits_a^\infty F\cdot g'</math>. נראה שכל אחד מהמחוברים באגף ימין הם גבולות מתכנסים | + | לכל <math>x>a</math> נגדיר <math>F(x)=\int\limits_a^x f</math>. כיוון ש-f רציפה המשפט היסודי אומר ש-<math>F'(x)=f(x)</math> לכל <math>x>a</math>. יתר על כן, הנתונים שלנו גוררים ש-<math>\forall x>a:\ |F(x)|\le M</math>. כעת <math>\int\limits_a^\infty f\cdot g=\left[F(x)g(x)\right]_{x=a}^\infty-\int\limits_a^\infty F\cdot g'</math>. נראה שכל אחד מהמחוברים באגף ימין הם גבולות מתכנסים: <math>\lim_{R\to\infty} [F(x)g(x)]_{x=a}^R=\lim_{R\to\infty} \underbrace{F(R)}_\text{bounded}\underbrace{g(R)}_{\to0}-\underbrace{F(a)}_0g(a)=0</math>. נותר להוכיח שקיים <math>\lim_{R\to\infty}\int\limits_a^R F\cdot g'</math>, ז"א צריך להוכיח שהאינטגרל <math>\int\limits_a^\infty F\cdot g'</math> מתכנס. עפ"י משפט 8 מספיק להראות שהאינטגרל הזה מתכנס בהחלט. נתון ש-g מונוטונית ולכן <math>g'(x)\ge0</math> לכל <math>x>a</math> או <math>g'(x)\le0</math> לכל <math>x>a</math>. נניח ש-<math>\forall x>a:\ g'(x)\ge0</math> (ההוכחה במקרה השני דומה). יוצא שלכל <math>x>a</math> מתקיים <math>0\le|F(x)g'(x)|=|F(x)|g'(x)\le Mg'(x)</math> ושהאינטגרל של <math>Mg'(x)</math> הוא <math>\int\limits_a^\infty Mg'=[Mg(x)]_{x=a}^\infty=0-Mg(a)</math> כי נתון ש-<math>\lim_{x\to\infty} g(x)=0</math>. לסיכום הראנו ש-<math>\int\limits_a^\infty Mg'</math> מתכנס. ממבחן ההשוואה נסיק שמתכנס <math>\int\limits_a^\infty |F|\cdot g'</math> ולכן מתכנס <math>\int\limits_a^\infty F\cdot g'</math>. לכן קיים <math>\lim_{R\to\infty}\int\limits_a^R F\cdot g'</math> וסיימנו את ההוכחה. {{משל}} |
===דוגמאות=== | ===דוגמאות=== | ||
| − | * נראה כי לכל <math>\alpha>0</math> האינטגרל <math>\int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\mathrm dx</math> מתכנס: נגדיר <math>f(x)=\sin(x)\ \and\ g(x)=\frac1{x^\alpha}</math>. מכאן נובע כי ל-f יש אינטגרלים חלקיים חסומים: <math>\left|\int\limits_1^b f\right|=\left|\int\limits_1^b \sin\right|=\left|[-\cos(x)]_{x=1}^b\right|=|-\cos(b)+\cos(1)|\le2</math>. יתר על כן <math>g(x)=\frac1{x^\alpha}</math> פונקציה מונוטונית יורדת ובעלת נגזרת רציפה <math>-\alpha x^{-\alpha-1}</math> בקטע <math>[1,\infty)</math> ומתקיים <math>\lim_{x\to\infty} g(x)=0</math>. קיימנו את תנאי מבחן דיריכלה ולכן האינטגרל מתכנס. {{משל}} | + | * נראה כי לכל <math>\alpha>0</math> האינטגרל <math>\int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\mathrm dx</math> מתכנס: נגדיר <math>f(x)=\sin(x)\ \and\ g(x)=\frac1{x^\alpha}</math>. מכאן נובע כי ל-f יש אינטגרלים חלקיים חסומים: <math>\left|\int\limits_1^b f\right|=\left|\int\limits_1^b \sin\right|=\left|[-\cos(x)]_{x=1}^b\right|=|-\cos(b)+\cos(1)|\le2</math>. יתר על כן, <math>g(x)=\frac1{x^\alpha}</math> פונקציה מונוטונית יורדת ובעלת נגזרת רציפה <math>-\alpha x^{-\alpha-1}</math> בקטע <math>[1,\infty)</math> ומתקיים <math>\lim_{x\to\infty} g(x)=0</math>. קיימנו את תנאי מבחן דיריכלה ולכן האינטגרל מתכנס. {{משל}} |
| − | * נוכיח ש-<math>\int\limits_1^\infty\frac{\sin(x)}x\mathrm dx</math> אינו מתכנס בהחלט, ולמעשה <math>\int\limits_1^\infty\left|\frac{\sin(x)}x\right|\mathrm dx=\infty</math>: לכל <math>x\ge1</math>, מכיוון ש-<math>|\sin(x)|\le1</math>, <math>0\le\frac{\sin^2(x)}x\le\left|\frac{\sin(x)}x\right|</math>. ע"פ מבחן ההשוואה מספיק להראות ש-<math>\int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx</math> מתבדר. נעזר בזהות <math>\sin^2(x)=\frac{1-\cos(2x)}2</math> להראות ש-<math>\int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx=\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx</math>. קל להראות (בעזרת מבחן דיריכלה) כי <math>\int\limits_1^\infty\frac{\cos(2x)}{2x}\mathrm dx</math> מתכנס. כמו כן ידוע לנו כי <math>\int\limits_1^\infty\frac{\mathrm dx}{2x}=\infty</math>. עתה נניח בשלילה ש-<math>\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx</math> מתכנס. לפי משפט 1 <math>\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx+\int\limits_1^\infty\frac{\cos(2x)}{2x}\mathrm dx=\int\limits_1^\infty\frac{\mathrm dx}{2x}</math>, אבל זהו סכום של אינטגרלים מתכנסים השווה לאינטגרל שמתבדר, בסתירה. {{משל}} | + | * נוכיח ש-<math>\int\limits_1^\infty\frac{\sin(x)}x\mathrm dx</math> אינו מתכנס בהחלט, ולמעשה <math>\int\limits_1^\infty\left|\frac{\sin(x)}x\right|\mathrm dx=\infty</math>: לכל <math>x\ge1</math>, מכיוון ש-<math>|\sin(x)|\le1</math>, <math>0\le\frac{\sin^2(x)}x\le\left|\frac{\sin(x)}x\right|</math>. ע"פ מבחן ההשוואה מספיק להראות ש-<math>\int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx</math> מתבדר. נעזר בזהות <math>\sin^2(x)=\frac{1-\cos(2x)}2</math> להראות ש-<math>\int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx=\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx</math>. קל להראות (בעזרת מבחן דיריכלה) כי <math>\int\limits_1^\infty\frac{\cos(2x)}{2x}\mathrm dx</math> מתכנס. כמו כן, ידוע לנו כי <math>\int\limits_1^\infty\frac{\mathrm dx}{2x}=\infty</math>. עתה נניח בשלילה ש-<math>\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx</math> מתכנס. לפי משפט 1 <math>\int\limits_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx+\int\limits_1^\infty\frac{\cos(2x)}{2x}\mathrm dx=\int\limits_1^\infty\frac{\mathrm dx}{2x}</math>, אבל זהו סכום של אינטגרלים מתכנסים השווה לאינטגרל שמתבדר, בסתירה. {{משל}} |
| שורה 32: | שורה 32: | ||
כהשלמה לאינפי 1 נביא את משפט דיריכלה להתכנסות טורים. | כהשלמה לאינפי 1 נביא את משפט דיריכלה להתכנסות טורים. | ||
| − | בהוכחה נשתמש בסכימה בחלקים, שדומה לאינטגרציה בחלקים. | + | בהוכחה נשתמש בסכימה בחלקים, שדומה לאינטגרציה בחלקים. נתבונן בסכום <math>\sum_{n=1}^N a_nb_n</math> ונגדיר סכומים חלקיים <math>S_n=\sum_{k=1}^n a_k</math>. מכאן <math>\forall n:\ a_n=S_n-S_{n-1}</math>. נקבל {{left|<math>\begin{align}\sum_{n=1}^N a_nb_n&=S_1b_1+(S_2-S_1)b_2+(S_3-S_2)b_3+\dots+(S_N-S_{N-1})b_N\\&=S_1(b_1-b_2)+S_2(b_2-b_3)+\dots+S_{N-1}(b_{N-1}-b_N)+S_Nb_N\end{align}</math>}}ז"א <math>\sum_{n=1}^Na_nb_n=\sum_{n=1}^{N-1}S_n(b_n-b_{n+1})+S_Nb_N</math>, מה שנקרא סכימה בחלקים. |
==משפט 10 {{הערה|(משפט דיריכלה לטורים)}}== | ==משפט 10 {{הערה|(משפט דיריכלה לטורים)}}== | ||
| שורה 59: | שורה 59: | ||
משפט לייבניץ הוא מקרה פרטי של משפט דיריכלה: נגדיר <math>a_n=(-1)^{n+1}</math> (ולכן הסכומים החלקיים חסומים). מכאן נובע שעבור <math>b_n</math> מונוטונית יורדת שואפת לאפס הטור <math>\sum_{n=1}^\infty a_n b_n</math>, שהוא טור לייבניץ, מתכנס. | משפט לייבניץ הוא מקרה פרטי של משפט דיריכלה: נגדיר <math>a_n=(-1)^{n+1}</math> (ולכן הסכומים החלקיים חסומים). מכאן נובע שעבור <math>b_n</math> מונוטונית יורדת שואפת לאפס הטור <math>\sum_{n=1}^\infty a_n b_n</math>, שהוא טור לייבניץ, מתכנס. | ||
===דוגמה=== | ===דוגמה=== | ||
| − | נניח ש-<math>\{b_n\}</math> יורדת לאפס ונראה שהטור <math>\sum_{n=1}^\infty\cos(n)b_n</math> מתכנס. נגדיר <math>a_n=\cos(n)</math> ולכן מספיק להראות שהסכומים החלקיים <math>\sum_{n=1}^N a_n</math> חסומים. נסתמך על זהות טריגונומטרית האומרת ש-<math>\cos(\alpha)\sin(\beta)=\frac12\sin(\alpha+\beta)-\frac12\sin(\alpha-\beta)</math>. לפי זה לכל n מתקיים <math>\cos(n)\sin\left(\frac12\right)=\frac12\sin(n+ | + | נניח ש-<math>\{b_n\}</math> יורדת לאפס ונראה שהטור <math>\sum_{n=1}^\infty\cos(n)b_n</math> מתכנס. נגדיר <math>a_n=\cos(n)</math> ולכן מספיק להראות שהסכומים החלקיים <math>\sum_{n=1}^N a_n</math> חסומים. נסתמך על זהות טריגונומטרית האומרת ש-<math>\cos(\alpha)\sin(\beta)=\frac12\sin(\alpha+\beta)-\frac12\sin(\alpha-\beta)</math>. לפי זה לכל n מתקיים <math>\cos(n)\sin\left(\frac12\right)=\frac12\sin\left(n+\frac12\right)-\frac12\sin\left(n-\frac12\right)</math>. לכן |
{| | {| | ||
{{=|l=\sum_{n=1}^N\cos(n) | {{=|l=\sum_{n=1}^N\cos(n) | ||
| − | |r=\frac1{\sin(1/2)}\sum_{n=1}^N\frac12(\sin(n+ | + | |r=\frac1{\sin(1/2)}\sum_{n=1}^N\frac12\left(\sin\left(n+\frac12\right)-\sin\left(n-\frac12\right)\right) |
}} | }} | ||
{{=|r=-\frac12\frac{\sin(1-1/2)}{\sin(1/2)}+\frac12\frac{\sin(N+1/2)}{\sin(1/2)} | {{=|r=-\frac12\frac{\sin(1-1/2)}{\sin(1/2)}+\frac12\frac{\sin(N+1/2)}{\sin(1/2)} | ||
גרסה מ־17:38, 31 ביולי 2011
את משפט 7 לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-12.4.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.
תוכן עניינים
אינטגרל לא אמיתי, סוג I (המשך)
הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב-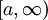 . נאמר ש-
. נאמר ש-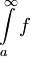 מתכנס בהחלט אם
מתכנס בהחלט אם 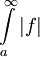 מתכנס. אם האינטגרל מתכנס אבל לא בהחלט נאמר שהוא מתכנס בתנאי.
מתכנס. אם האינטגרל מתכנס אבל לא בהחלט נאמר שהוא מתכנס בתנאי.
משפט 8
תהי f מוגדרת ואינטגרבילית מקומית ב-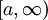 . אם
. אם 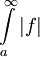 מתכנס אז
מתכנס אז 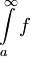 מתכנס. במילים: אם f אינטגרבילית בהחלט בקטע
מתכנס. במילים: אם f אינטגרבילית בהחלט בקטע 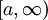 אז f אינטגרבילית בקטע.
אז f אינטגרבילית בקטע.
הוכחה
לפי המסקנה למשפט 7 מספיק להוכיח ש-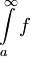 מקיים את תנאי קושי. לצורך זה יהי
מקיים את תנאי קושי. לצורך זה יהי  נתון. כיוון ש-
נתון. כיוון ש-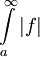 מתכנס הוא מקיים את תנאי קושי וקיים
מתכנס הוא מקיים את תנאי קושי וקיים 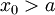 כך שאם
כך שאם 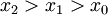 אז
אז 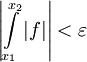 . נובע מיד ש-
. נובע מיד ש-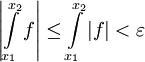 . קיימנו את תנאי קושי ל-
. קיימנו את תנאי קושי ל-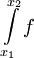 ולכן הוא מתכנס.
ולכן הוא מתכנס. 
גישה אחרת: נגדיר 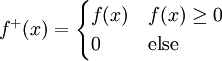 וכן
וכן 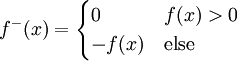 . לכן
. לכן 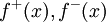 אי-שליליות. קל להראות שלכל x,
אי-שליליות. קל להראות שלכל x, 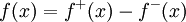 וכן
וכן 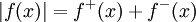 (גאומטרית:
(גאומטרית: 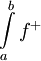 השטח שמעל ציר ה-x ו-
השטח שמעל ציר ה-x ו-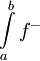 השטח שמתחת).
השטח שמתחת).
כעת, אם נתון ש-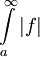 מתכנס, מבחן ההשוואה אומר שכיוון ש-
מתכנס, מבחן ההשוואה אומר שכיוון ש-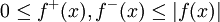 שני האינטגרלים
שני האינטגרלים 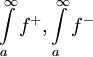 מתכנסים ונובע ממשפט 1 ש-
מתכנסים ונובע ממשפט 1 ש-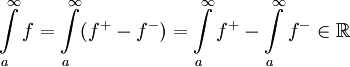 , כלומר
, כלומר 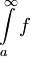 מתכנס.
מתכנס. 
דוגמאות
-
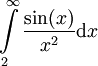 - מתכנס או מתבדר? נראה התכנסות ע"י הוכחת התכנסות בהחלט:
- מתכנס או מתבדר? נראה התכנסות ע"י הוכחת התכנסות בהחלט: 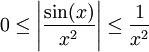 ולכן, עפ"י מבחן ההשוואה עם
ולכן, עפ"י מבחן ההשוואה עם 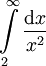 ,
, 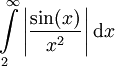 מתכנס.
מתכנס. 
- נבנה דוגמאות של f מוגדרת ורציפה ב-
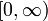 כך ש-
כך ש-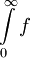 מתכנס אעפ"י ש-
מתכנס אעפ"י ש-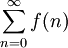 מתבדר, ולהיפך:
מתבדר, ולהיפך: 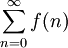 מתכנס ואילו
מתכנס ואילו 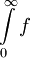 מתבדר. ובכן, אם
מתבדר. ובכן, אם 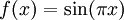 אז
אז ![\int\limits_0^\infty f=\lim_{R\to\infty}\int\limits_0^R\sin(\pi x)\mathrm dx=\lim_{R\to\infty}\left[\frac{-\cos(\pi x)}\pi\right]_{x=0}^R](/images/math/f/0/8/f0887ce8f0a8236594ee04c48e779c3c.png) ואין גבול, לכן האינטגרל מתבדר. לעומת זאת,
ואין גבול, לכן האינטגרל מתבדר. לעומת זאת, 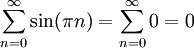 , שבוודאי מתכנס. לצד השני נגדיר פונקציה f ע"י הגרף
, שבוודאי מתכנס. לצד השני נגדיר פונקציה f ע"י הגרף 
אזי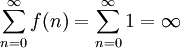 - מתבדר. לעומת זאת,
- מתבדר. לעומת זאת, 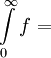 השטח שמתחת לגרף
השטח שמתחת לגרף 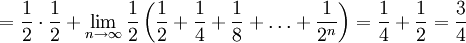

משפט 9 (מבחן דיריכלה)
נניח ש-f מוגדרת ורציפה ב-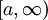 ונניח שהאינטגרלים החלקיים
ונניח שהאינטגרלים החלקיים  חסומים כאשר
חסומים כאשר 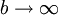 (ז"א קיים
(ז"א קיים 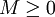 כך ש-
כך ש-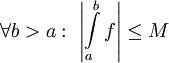 ). עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב-
). עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב-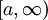 ו-
ו-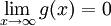 אזי
אזי 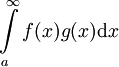 מתכנס.
מתכנס.
הוכחה
לכל 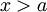 נגדיר
נגדיר 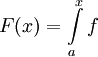 . כיוון ש-f רציפה המשפט היסודי אומר ש-
. כיוון ש-f רציפה המשפט היסודי אומר ש-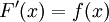 לכל
לכל 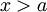 . יתר על כן, הנתונים שלנו גוררים ש-
. יתר על כן, הנתונים שלנו גוררים ש-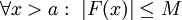 . כעת
. כעת ![\int\limits_a^\infty f\cdot g=\left[F(x)g(x)\right]_{x=a}^\infty-\int\limits_a^\infty F\cdot g'](/images/math/a/b/6/ab6aa2f4ea3f9863af9640e829e5bf85.png) . נראה שכל אחד מהמחוברים באגף ימין הם גבולות מתכנסים:
. נראה שכל אחד מהמחוברים באגף ימין הם גבולות מתכנסים: ![\lim_{R\to\infty} [F(x)g(x)]_{x=a}^R=\lim_{R\to\infty} \underbrace{F(R)}_\text{bounded}\underbrace{g(R)}_{\to0}-\underbrace{F(a)}_0g(a)=0](/images/math/a/e/3/ae34cc67126220653434348135942fc0.png) . נותר להוכיח שקיים
. נותר להוכיח שקיים 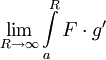 , ז"א צריך להוכיח שהאינטגרל
, ז"א צריך להוכיח שהאינטגרל 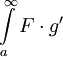 מתכנס. עפ"י משפט 8 מספיק להראות שהאינטגרל הזה מתכנס בהחלט. נתון ש-g מונוטונית ולכן
מתכנס. עפ"י משפט 8 מספיק להראות שהאינטגרל הזה מתכנס בהחלט. נתון ש-g מונוטונית ולכן 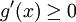 לכל
לכל 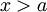 או
או 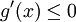 לכל
לכל 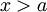 . נניח ש-
. נניח ש-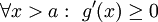 (ההוכחה במקרה השני דומה). יוצא שלכל
(ההוכחה במקרה השני דומה). יוצא שלכל 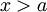 מתקיים
מתקיים 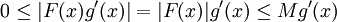 ושהאינטגרל של
ושהאינטגרל של 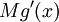 הוא
הוא ![\int\limits_a^\infty Mg'=[Mg(x)]_{x=a}^\infty=0-Mg(a)](/images/math/a/6/a/a6a1536516cd30bbd8ae2f63490ccce5.png) כי נתון ש-
כי נתון ש-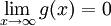 . לסיכום הראנו ש-
. לסיכום הראנו ש-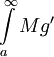 מתכנס. ממבחן ההשוואה נסיק שמתכנס
מתכנס. ממבחן ההשוואה נסיק שמתכנס 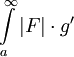 ולכן מתכנס
ולכן מתכנס 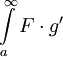 . לכן קיים
. לכן קיים 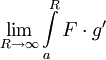 וסיימנו את ההוכחה.
וסיימנו את ההוכחה. 
דוגמאות
- נראה כי לכל
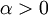 האינטגרל
האינטגרל 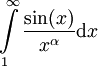 מתכנס: נגדיר
מתכנס: נגדיר 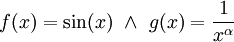 . מכאן נובע כי ל-f יש אינטגרלים חלקיים חסומים:
. מכאן נובע כי ל-f יש אינטגרלים חלקיים חסומים: ![\left|\int\limits_1^b f\right|=\left|\int\limits_1^b \sin\right|=\left|[-\cos(x)]_{x=1}^b\right|=|-\cos(b)+\cos(1)|\le2](/images/math/1/2/2/122de72231e8859f53630c9080c0943a.png) . יתר על כן,
. יתר על כן, 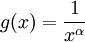 פונקציה מונוטונית יורדת ובעלת נגזרת רציפה
פונקציה מונוטונית יורדת ובעלת נגזרת רציפה 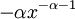 בקטע
בקטע 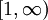 ומתקיים
ומתקיים 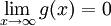 . קיימנו את תנאי מבחן דיריכלה ולכן האינטגרל מתכנס.
. קיימנו את תנאי מבחן דיריכלה ולכן האינטגרל מתכנס. 
- נוכיח ש-
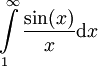 אינו מתכנס בהחלט, ולמעשה
אינו מתכנס בהחלט, ולמעשה 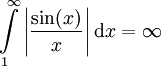 : לכל
: לכל 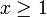 , מכיוון ש-
, מכיוון ש-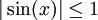 ,
, 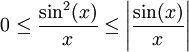 . ע"פ מבחן ההשוואה מספיק להראות ש-
. ע"פ מבחן ההשוואה מספיק להראות ש-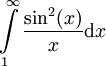 מתבדר. נעזר בזהות
מתבדר. נעזר בזהות 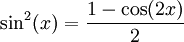 להראות ש-
להראות ש-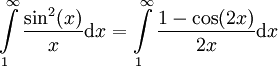 . קל להראות (בעזרת מבחן דיריכלה) כי
. קל להראות (בעזרת מבחן דיריכלה) כי 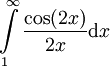 מתכנס. כמו כן, ידוע לנו כי
מתכנס. כמו כן, ידוע לנו כי 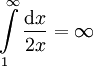 . עתה נניח בשלילה ש-
. עתה נניח בשלילה ש-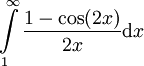 מתכנס. לפי משפט 1
מתכנס. לפי משפט 1 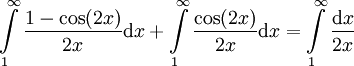 , אבל זהו סכום של אינטגרלים מתכנסים השווה לאינטגרל שמתבדר, בסתירה.
, אבל זהו סכום של אינטגרלים מתכנסים השווה לאינטגרל שמתבדר, בסתירה. 
כהשלמה לאינפי 1 נביא את משפט דיריכלה להתכנסות טורים.
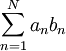 ונגדיר סכומים חלקיים
ונגדיר סכומים חלקיים 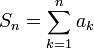 . מכאן
. מכאן 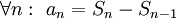 . נקבל
. נקבל 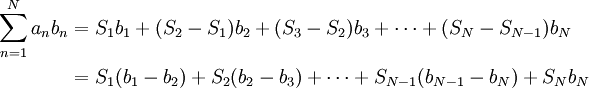
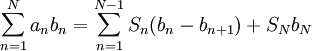 , מה שנקרא סכימה בחלקים.
, מה שנקרא סכימה בחלקים.
משפט 10 (משפט דיריכלה לטורים)
נניח שלטור 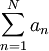 יש סכומים חלקיים
יש סכומים חלקיים 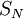 חסומים (כלומר
חסומים (כלומר 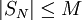 ). עוד נניח ש-
). עוד נניח ש-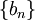 סדרה מונוטונית כך ש-
סדרה מונוטונית כך ש-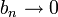 . אז
. אז 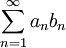 מתכנס.
מתכנס.
את ההמשך עשינו בהרצאה שאחריה:
הוכחה
לכל N מתקיים 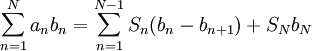 . נשאיף
. נשאיף 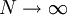 אזי
אזי 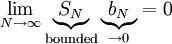 . נותר להוכיח ש-
. נותר להוכיח ש-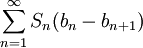 מתכנס, ונעשה זאת ע"י כך שנראה שהוא מתכנס בהחלט.
מתכנס, ונעשה זאת ע"י כך שנראה שהוא מתכנס בהחלט.
נסמן c כ-1 אם 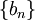 יורדת ו- יורדת ו-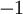 אחרת: אחרת:
|
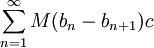
|
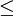
|
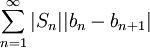
|
|||
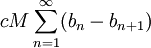
|

|
|||||
| הטור טלסקופי. | 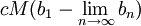
|

|
||||
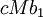
|

|
כלומר הסכום מתכנס. 
הערה
משפט לייבניץ הוא מקרה פרטי של משפט דיריכלה: נגדיר 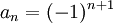 (ולכן הסכומים החלקיים חסומים). מכאן נובע שעבור
(ולכן הסכומים החלקיים חסומים). מכאן נובע שעבור  מונוטונית יורדת שואפת לאפס הטור
מונוטונית יורדת שואפת לאפס הטור 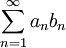 , שהוא טור לייבניץ, מתכנס.
, שהוא טור לייבניץ, מתכנס.
דוגמה
נניח ש-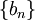 יורדת לאפס ונראה שהטור
יורדת לאפס ונראה שהטור 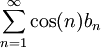 מתכנס. נגדיר
מתכנס. נגדיר 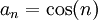 ולכן מספיק להראות שהסכומים החלקיים
ולכן מספיק להראות שהסכומים החלקיים 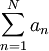 חסומים. נסתמך על זהות טריגונומטרית האומרת ש-
חסומים. נסתמך על זהות טריגונומטרית האומרת ש-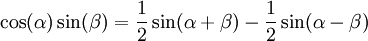 . לפי זה לכל n מתקיים
. לפי זה לכל n מתקיים 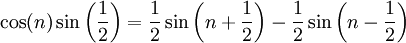 . לכן
. לכן
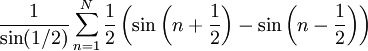
|

|
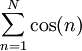
|
||||
| הטור טלסקופי, לכן: | 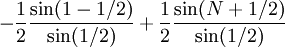
|

|
||||
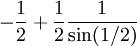
|
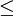
|
