משתמש:אור שחף/133 - הרצאה/12.4.11
תוכן עניינים
משפט 7
תהי F מוגדרת בקטע  אז
אז 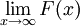 קיים ממש אם"ם F מקיימת את תנאי קושי ב-
קיים ממש אם"ם F מקיימת את תנאי קושי ב- .
.
=הוכחה
אם ידוע ש-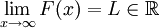 קל לקיים את תנאי קושי וכבר עשינו זאת. לצד השני נניח שתנאי קושי מתקיים עבור F. תחילה נראה ש-F חסומה ב-
קל לקיים את תנאי קושי וכבר עשינו זאת. לצד השני נניח שתנאי קושי מתקיים עבור F. תחילה נראה ש-F חסומה ב- . מתנאי קושי נובע שקיים
. מתנאי קושי נובע שקיים 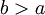 כך שלכל
כך שלכל 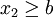 ,
, 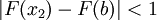 . מכאן שלכל
. מכאן שלכל 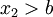
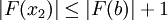 . לכן F חסומה בקטע
. לכן F חסומה בקטע 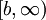 . כעת נתבונן בסדרת הערכים
. כעת נתבונן בסדרת הערכים 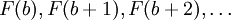 . זאת סדרה חסומה. עפ"י בולצאנו וירשטרס קיימת לה תת סדרה מתכנסת
. זאת סדרה חסומה. עפ"י בולצאנו וירשטרס קיימת לה תת סדרה מתכנסת 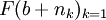 כאשר
כאשר 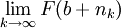 קיים ונקרא לו L.
טענה:
קיים ונקרא לו L.
טענה: 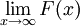 קיים ושווה ל-L. הוכחה: יהי
קיים ושווה ל-L. הוכחה: יהי 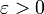 נתון. כיוון ש-
נתון. כיוון ש-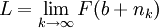 קיים
קיים 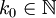 כך שלכל
כך שלכל 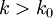 ,
, 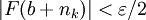 . כמו כן, עפ"י תנאי קושי קיים
. כמו כן, עפ"י תנאי קושי קיים 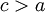 כך שאם
כך שאם 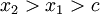 אז
אז 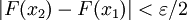 . נגדיר
. נגדיר 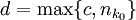 . צ"ל: לכל
. צ"ל: לכל 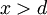 ,
, 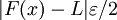 , מה שגורר
, מה שגורר 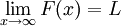 . ובכן אם
. ובכן אם 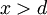 נוכל לבחור
נוכל לבחור 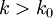 כך ש-
כך ש-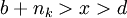 (כי
(כי ![b+n_k\xleftarrow[k\to\infty]{}\infty](/images/math/a/7/0/a702e409ce6a0c69655e07cbb29509c7.png) ). כעת לפי הבניה שלנו
). כעת לפי הבניה שלנו 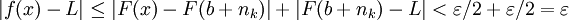 . נובע ש-
. נובע ש-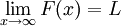 .
. 
מסקנה
תהי f מוגדרת ואינטגרבילית מקומית ב- . אזי האינטגרל עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \in\limits_a^\infty f
. אזי האינטגרל עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \in\limits_a^\infty f
מתכנס אם"ם האינטגרל מקיים את תנאי קושי: לכלקיים
כך שאם
אז
.
הוכחה
לכל 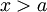 נגדיר
נגדיר 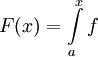 . לפי ההגדרה
. לפי ההגדרה 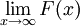 מתכנס אם"ם
מתכנס אם"ם 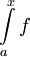 מתכנס...
מתכנס...
הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב- נאמר ש-
נאמר ש-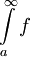 מתכנס בהחלט אם
מתכנס בהחלט אם 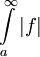 מתכנס. אם האינטגרל מתכנס לא בהחלט נאמר שהוא מתכנס בתנאי.
מתכנס. אם האינטגרל מתכנס לא בהחלט נאמר שהוא מתכנס בתנאי.
משפט 8
תהי f מוגדר ואינטגרבילית מקומית ב- . אם
. אם 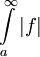 אז
אז 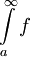 מתכנס. במילים: אם f אינטגרבילית בהחלט ב-
מתכנס. במילים: אם f אינטגרבילית בהחלט ב- אז f אינטגרבילית שם.
אז f אינטגרבילית שם.
הוכחה
לפי המסקנה למשפט 7 מספיק להוכיח ש-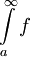 מקיים את תנאי קושי. לצורך זה יהי
מקיים את תנאי קושי. לצורך זה יהי 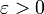 נתון. כיוון ש-
נתון. כיוון ש-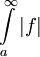 מתכנס אז הוא מקיים את תנאי קושי וקיים
מתכנס אז הוא מקיים את תנאי קושי וקיים 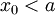 כך שאם
כך שאם 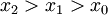 אז
אז 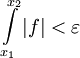 . נובע מיד ש-
. נובע מיד ש-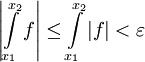 . קיימנו את תנאי קושי ל-
. קיימנו את תנאי קושי ל-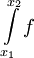 ולכן הוא מתכנס.
ולכן הוא מתכנס.  גישה אחרת: נגדיר
גישה אחרת: נגדיר 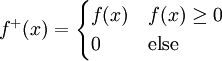 וכן
וכן 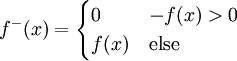 . לכן
. לכן  לא שליליות. בודקים שלכל x
לא שליליות. בודקים שלכל x 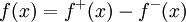 וכן
וכן 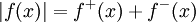 . (גאומטרית:
. (גאומטרית: 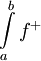 השטח שמעל ציר ה-x ו-
השטח שמעל ציר ה-x ו-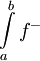 השטח שמתחת)
כעת אם נתון ש-עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limit_a^\infty|f|
השטח שמתחת)
כעת אם נתון ש-עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limit_a^\infty|f|
מתכנס. מבחן ההשוואה אומר שכיוון ש-...
עכשיו נובע ממשפט 1 ש-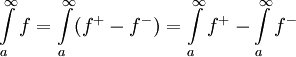 ...
...
דוגמאות
- ...
- נבנה דוגמאות של f מוגדרת ורציפה ב-
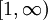 כך ש-
כך ש-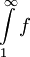 מתכנס אעפ"י ש-
מתכנס אעפ"י ש-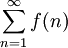 , ולהיפך:
, ולהיפך: 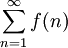 מתכנס ואילו
מתכנס ואילו 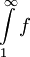 מתבדר. ובכן אם
מתבדר. ובכן אם 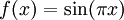 אז
אז ![\int\limits_0^\infty f=\lim_{R\to\infty}\int\limits_0^R\sin(\pi x)\mathrm dx=\lim_{R\to\infty}\left[\frac{-\cos(\pi x)}\pi\right]_{x=0}^R](/images/math/f/0/8/f0887ce8f0a8236594ee04c48e779c3c.png) ואין גבול. לכל האינטגרל מתבדר. לעומת זאת,
ואין גבול. לכל האינטגרל מתבדר. לעומת זאת, 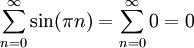 , שבוודאי מתכנס. לצד השני נגדיר f ע"י גרף (יטופל בהמשך) moveTo(1/2,0);lineTo(1,1);lineTo(3/2,0);lineTo(7/4,0);lineTo(2,1);lineTo(9/4,0);lineTo(25/8,0);...
, שבוודאי מתכנס. לצד השני נגדיר f ע"י גרף (יטופל בהמשך) moveTo(1/2,0);lineTo(1,1);lineTo(3/2,0);lineTo(7/4,0);lineTo(2,1);lineTo(9/4,0);lineTo(25/8,0);...
משפט 9 (מבחן דיריכלה)
נניח ש-f מוגדרת ורציפה ב- ונניח שהאינטגרלים החלקיים
ונניח שהאינטגרלים החלקיים 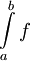 חסומים כאשר
חסומים כאשר 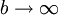 . ז"א קיים
. ז"א קיים 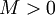 כך שלכל
כך שלכל 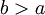
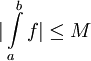 . עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב-
. עוד נניח ש-g מוגדרת, מונוטונית ובעלת נגזרת רציפה ב- ו-
ו-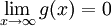 אזי
אזי 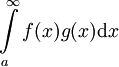 מתכנס.
מתכנס.
הוכחה
לכל 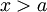 נגדיר
נגדיר 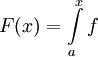 . כיוון ש-f רציפה המשפט היסודי אומר ש-
. כיוון ש-f רציפה המשפט היסודי אומר ש-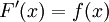 לכל
לכל 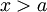 . יתר על כן, הנתונים שלנו גוררים שלכל
. יתר על כן, הנתונים שלנו גוררים שלכל 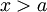
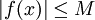 . כעת
. כעת ![\int\limits_a^\infty f\cdot g=\lim_{R\to\infty}\int\limits_a^Rf\cdot g=\lim_{R\to\infty}\left[F(x)g(x)\right]_{x=a}^R-\int\limits_a^\infty F\cdot g'](/images/math/c/7/0/c70567a2b05caba5becae0671486fd52.png) . נראה שלכל אחד מהביטויים הנ"ל יש גבול כאשר
. נראה שלכל אחד מהביטויים הנ"ל יש גבול כאשר 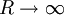 . ובכן עיבוד הנוסחה נכשל (שגיאת תחביר): \lim_{R\to\infty} [F(x)g(x)]_{x=a]^R=\lim_{R\to\infty} \underbrace{F(R)}_\text{bounded}\underbrace{g(R)}_{\to0}-\underbrace{F(a)}_0g(a)=0
. נותר להוכיח שקיים
. ובכן עיבוד הנוסחה נכשל (שגיאת תחביר): \lim_{R\to\infty} [F(x)g(x)]_{x=a]^R=\lim_{R\to\infty} \underbrace{F(R)}_\text{bounded}\underbrace{g(R)}_{\to0}-\underbrace{F(a)}_0g(a)=0
. נותר להוכיח שקיים 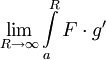 . ז"א צריך להוכיח שהאינטגרל עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limit_a^\infty F\cdot g'
. ז"א צריך להוכיח שהאינטגרל עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limit_a^\infty F\cdot g'
מתכנס עפ"י משפט 8 מספיק להראות שהאינטגרל הזה מתכנס בהחלט. נתון ש-g מונוטונית ולכןלכל
או
לכל
. כמקרה ראשון נניח ש-
. יוצא שלכל
מתקיים
ושהאינטגרל של
הוא
כי נתון ש-
בסיכון הראנו ש-
מתכנס. ממבחן ההשוואה נסיק שמתכנס
ולכן מתכנס
. לכן קיים
וסיימנו את ההוכחה.

דוגמה: לכל 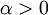
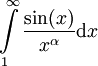 . הוכחה: נגדיר
. הוכחה: נגדיר 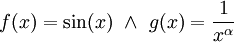 . אז ל-f יש אינטגרלים חלקיים חסומים:
. אז ל-f יש אינטגרלים חלקיים חסומים: ![|\int\limits_1^b f|=|\int\limits_1^b \sin|=|[-\cos(x)]_{x=1}^b|=|-\cos(b)+\cos(1)|\le2](/images/math/0/e/6/0e6e0e99be073b439c70d7b04dcf2047.png) . יתר על כן
. יתר על כן 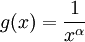 פונקציה מונוטונית יורדת ובעלת נגזרת רציפה עיבוד הנוסחה נכשל (פונקציה \alphax לא מוכרת): -\alphax^{-\alpha-1}
פונקציה מונוטונית יורדת ובעלת נגזרת רציפה עיבוד הנוסחה נכשל (פונקציה \alphax לא מוכרת): -\alphax^{-\alpha-1}
בקטעמתקיים
ז"א 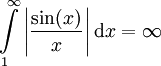 אבל לכל
אבל לכל 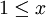
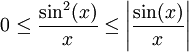 כי
כי 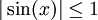 ולכן
ולכן 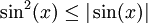 ואילו
ואילו 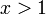 ולא מושפע ע"י הערך המוחלט. עפ"י מבחן ההשוואה מספיק להוכיח ש-
ולא מושפע ע"י הערך המוחלט. עפ"י מבחן ההשוואה מספיק להוכיח ש-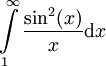 מתבדר. אמנם
מתבדר. אמנם 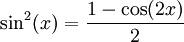 ולכן עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx=\int\limit_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx
ולכן עיבוד הנוסחה נכשל (פונקציה \limit לא מוכרת): \int\limits_1^\infty\frac{\sin^2(x)}x\mathrm dx=\int\limit_1^\infty\frac{1-\cos(2x)}{2x}\mathrm dx
שמתכנס עפ"י דיריכלה באותו נימוק כמו זה שהבאנו לאינטגרלוכידוע
מתבדר ל-
.
נוכיח בדרך השלילה שהאינטגרל שלנו 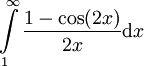 מתבדר. ובכן אם הוא מתכנס אז משפט אחד אומר ש-
מתבדר. ובכן אם הוא מתכנס אז משפט אחד אומר ש-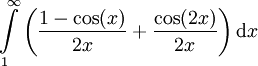 הוא סכום של אינטגרלים מתכנסים ולכן מתכנס. אבל סכום זה הוא
הוא סכום של אינטגרלים מתכנסים ולכן מתכנס. אבל סכום זה הוא 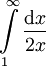 שמתבדר. הסתירה מוכיחה את הטענה.
שמתבדר. הסתירה מוכיחה את הטענה.
כהשלמה לאינפי 1 נביא את משפט דיריכלה להתכנסות טורים. בהוכחה נשתמש בסכימה בחלקים, שהיא דומה לאינטגרציה בחלקים. ובכן נתבונן בסכום 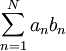 ונגדיר סכומים חלקיים
ונגדיר סכומים חלקיים 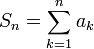 אז
אז 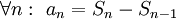 . אם כן
. אם כן 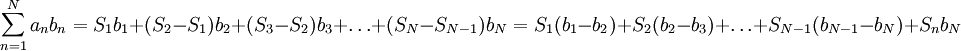 . ז"א
. ז"א 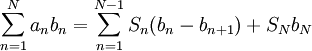 - סכימה בחלקים.
- סכימה בחלקים.
משפט 10 (משפט דיריכלה לטורים)
נתון 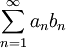 . נניח שלטור
. נניח שלטור 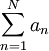 יש סכומים חלקיים חסומים
יש סכומים חלקיים חסומים 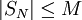 עוד נניח ש-
עוד נניח ש-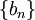 סדרה מונוטונית כך ש-
סדרה מונוטונית כך ש-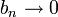 . אז
. אז 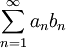 מתכנס.
מתכנס.