הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/15.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
(יצירת דף עם התוכן "דוגמה נוספת ל-<math>\int R(\cos(x),\sin(x))\mathrm dx</math>: <math>\int\frac{7\cos^3(x)\sin^2(x)-5\sin^4(x)}{2\cos^5(x)\sin^4(x)+4}\mathrm dx</math> י...") |
|||
| שורה 1: | שורה 1: | ||
| − | דוגמה נוספת ל-<math>\int R(\cos(x),\sin(x))\mathrm dx</math>: <math>\int\frac{7\cos^3(x)\sin^2(x)-5\sin^4(x)}{2\cos^5(x)\sin^4(x)+4}\mathrm dx</math> | + | =שיטות אינטגרציה {{הערה|(המשך)}}= |
| + | דוגמה נוספת ל-<math>\int R(\cos(x),\sin(x))\mathrm dx</math> (לא עלינו): <math>\int\frac{7\cos^3(x)\sin^2(x)-5\sin^4(x)}{2\cos^5(x)\sin^4(x)+4}\mathrm dx</math> | ||
| − | יש הצבה אוניברסלית: מציבים <math>t=\tan\left(\frac x2\right)</math> לכן <math>\mathrm dx=\frac{2\mathrm dt}{t^2+1}</math> וכן <math>\cos(x)=\frac{t^2 | + | יש הצבה אוניברסלית: מציבים <math>t=\tan\left(\frac x2\right)</math> לכן <math>\mathrm dx=\frac{2\mathrm dt}{t^2+1}</math> וכן <math>\cos(x)=\frac{1-t^2}{1+t^2}</math> ו-<math>\sin(x)=\frac{2t}{t^2+1}</math>. האינטגרל הופך לאינטגרל של פונקציה רציונלית של t (שאפשר לחשב עם שברים חלקיים). |
| − | ==דוגמאות | + | ==דוגמאות== |
| − | #<math>\int\frac{8\sin(x)-\cos(x)}{\sin(x)+2\cos(x)}\mathrm dx</math>: נציב t כנ"ל ונקבל <math>\int\frac{8\frac{2t}{1+t^2}-\frac{1-t^2}{1+t^2}}{\frac{2t}{1+t^2}+2\frac{1-t^2}{1+t^2}}\frac{2\mathrm dt}{1+t^2}=\int\frac{16t-1+t^2}{2t+2-2t^2}\cdot\frac{2\mathrm dt}{1+t^2}=-\int\frac{t^2+16t-1}{(t^2-t-1)(1+t^2)}\mathrm dt</math> ומכאן פותרים בשברים חלקיים. | + | #<math>\int\frac{8\sin(x)-\cos(x)}{\sin(x)+2\cos(x)}\mathrm dx</math>: נציב t כנ"ל ונקבל {{left|<math>\begin{align}\int\frac{8\frac{2t}{1+t^2}-\frac{1-t^2}{1+t^2}}{\frac{2t}{1+t^2}+2\frac{1-t^2}{1+t^2}}\cdot\frac{2\mathrm dt}{1+t^2}&=\int\frac{16t-1+t^2}{2t+2-2t^2}\cdot\frac{2\mathrm dt}{1+t^2}\\&=-\int\frac{t^2+16t-1}{(t^2-t-1)(1+t^2)}\mathrm dt\end{align}</math>}}ומכאן פותרים בשברים חלקיים.<br />''גישה יותר חכמה:'' מתקיים <math>R(-\cos(x),-\sin(x))=R(\cos(x),\sin(x))</math> ולכן נגדיר <math>t=\tan(x)\implies \mathrm dx=\frac{\mathrm dt}{1+t^2}</math>. האינטגרל הוא <math>\int\frac{8\tan(x)-1}{\tan(x)+2}\mathrm dx=\int\frac{8t-1}{t+2}\cdot\frac{\mathrm dt}{1+t^2}</math>. שוב פותרים שברים חלקיים, אלא שהפעם זה יותר פשוט. |
| − | #<math>\int\sec(x)\mathrm dx</math> ועם <math>t=\tan\left(\frac x2\right)</math> | + | # <math>\int\sec(x)\mathrm dx</math> ועם <math>t=\tan\left(\frac x2\right)</math> נקבל {{left|<math>\begin{align}\int&=\int\frac{1+t^2}{1-t^2}\frac{\mathrm dt}{1+t^2}\\&=\int\left(\frac{1/2}{1-t}+\frac{1/2}{1+t}\right)\mathrm dt\\&=-\frac12\ln|1-t|+\frac12\ln|1+t|+c\\&=\frac12\ln\left|\frac{1+\tan\left(\frac x2\right)}{1-\tan\left(\frac x2\right)}\right|+c\end{align}</math>}}''גישה אחרת:'' <math>\int=\int\frac{\cos(x)}{\cos^2(x)}\mathrm dx</math> נציב <math>y=\sin(x)</math> והאינטגרל הוא <math>\int\frac{\mathrm dy}{1-y^2}=\int\left(\frac{1/2}{1-y}+\frac{1/2}{1+y}\right)\mathrm dy=\frac12\ln\left|\frac{1+\sin(x)}{1-\sin(x)}\right|+c</math>.<br />''דרך המלך:'' <math>\int=\int\frac{\sec(x)(\sec(x)+\tan(x))}{\sec(x)+\tan(x)}\mathrm dx=\ln|\sec(x)+\tan(x)|+c</math>. |
| − | #<math>\int\sec^3(x)\mathrm dx</math> נציב <math>t=\tan( | + | # <math>\int\sec^3(x)\mathrm dx</math> נציב <math>t=\tan\left(\frac x2\right)</math> ונקבל <math>\int\frac{\left(1+t^2\right)^3}{\left(1-t^2\right)^3}\frac{2\mathrm dt}{1+t^2}=2\int\frac{\left(1+t^2\right)^2}{\left(1-t^2\right)^3}\mathrm dt</math> וניתן לעשות זאת, אבל זה לא נעים.<br />''דרך אחרת:'' <math>\int\frac{\cos(x)}{\cos^4(x)}\mathrm dx</math> ונציב <math>y=\sin(x)</math>. נקבל <math>\int\frac{\mathrm dy}{\left(1-y^2\right)^2}</math> וקל לפתור זאת ע"י שברים חלקיים.<br />''עוד דרך:''{{left|<math>\begin{align}\int&=\int\sec(x)\left(1+\tan^2(x)\right)\mathrm dx\\&=\int\sec(x)\mathrm dx+\int\sec(x)\tan(x)\mathrm dx\end{align}</math>}} נציב <math>y=\sin(x)</math> ושוב הגענו ל-<math>\int\frac{\mathrm dy}{\left(1-y^2\right)^2}</math>.<br />''ניסיון אחרון:''{{left|<math>\begin{align}\int&=\int\sec(x)\sec^2(x)\mathrm dx\\&=\sec(x)\tan(x)-\int\tan(x)\sec(x)\tan(x)\mathrm dx\\&=\sec(x)\tan(x)-\int\sec(x)(\sec^2(x)-1)\mathrm dx\\&=\sec(x)\tan(x)-\int\sec^3(x)\mathrm dx-\int\sec(x)\mathrm dx\end{align}</math><br /><math>\begin{array}{l l l}\implies&2\int\sec^3(x)\mathrm dx&=\sec(x)\tan(x)+\int\sec(x)\mathrm dx\\&&=\sec(x)\tan(x)+\ln|\sec(x)+\tan(x)|+c\end{array}</math>}} |
| − | + | ==אינטגרלים עם שורשים== | |
| − | לאינטגרל מהסוג <math>\int R\left(x,\left(\frac{ax+b}{cx+d}\right)^\frac nm | + | לאינטגרל מהסוג <math>\int R\left(x,\left(\frac{ax+b}{cx+d}\right)^\frac nm,\dots,\left(\frac{ax+b}{cx+d}\right)^\frac km\right)\mathrm dx</math>. תועיל הצבה: <math>\frac{ax+b}{cx+d}=t^m</math> |
| − | + | ===דוגמאות=== | |
| − | <math>\int\frac{\mathrm dx}{x(\sqrt x+\sqrt[5]{x^2})}=\int\frac{\mathrm dx}{x(x^\frac 5{10}+x^\frac | + | # <math>\int\frac{\mathrm dx}{x\left(\sqrt x+\sqrt[5]{x^2}\right)}=\int\frac{\mathrm dx}{x\left(x^\frac 5{10}+x^\frac 4{10}\right)}</math> נציב <math>x=t^{10}</math> אזי נקבל <math>\int\frac{10t^9\mathrm dt}{t^{10}(t^5+t^4)}=\int\frac{10\mathrm dt}{t^5(t+1)}</math> ופותרים בשברים חלקיים.<br />''דרך אחרת:'' <math>(1+t)(1-t+t^2-t^3+t^4)=1+t^5</math> (כי <math>1-t+t^2-t^3+t^4</math> טור הנדסי). לפי זה נקבל {{left|<math>\begin{align}\int\frac{10\mathrm dt}{t^5(t+1)}&=\int\left((1+t)(1-t+t^2-t^3+t^4)-t^5\right)\frac{10\mathrm dt}{(1+t)t^5}\\&=10\int\left(t^{-5}-t^{-4}+t^{-3}-t^{-2}+t^{-1}-(t+1)^{-1}\right)\mathrm dt\\&=\dots\end{align}</math>}} |
| − | #<math>\int\ | + | # <math>\int\sqrt[3]\frac{1-x}{1+x}\frac{\mathrm dx}x</math> נציב <math>t^3=\frac{1-x}{1+x}</math> ואז <math>x=\frac{1-t^3}{1+t^3}</math> וכך <math>\mathrm dx=\frac{(1+t^3)(-3t^2)-(1-t^3)(3t^2)}{\left(1+t^3\right)^2}\mathrm dt=\frac{-6t^2}{\left(1+t^3\right)^2}\mathrm dt</math> לכן <math>\int=\int t\frac{1+t^3}{1-t^3}\cdot\frac{-6t^2}{\left(1+t^3\right)^2}\mathrm dt=\int\frac{-6t^3\mathrm dt}{1-t^6}</math> נציב <math>y=t^2</math> ואז <math>\int=\int\frac{-3y\mathrm dy}{1-y^3}=\int\frac{-3y\mathrm dy}{(1-y)(1+y+y^2)}</math> ופותרים בשברים חלקיים. |
| − | + | ---- | |
| − | <math>\int \sqrt x(1+\sqrt[3]x)^4\mathrm dx</math> נציב <math>x=t^6</math> ונקבל <math>\int t^3(1+t^2)^4 | + | לאינטגרלים מהסוג <math>\int x^m(a+bx^n)^p\mathrm dx</math> עבור <math>a,b\in\mathbb R\ \and\ m,n,p\in\mathbb Q</math>: |
| − | + | * אם <math>p\in\mathbb Z</math> אז תועיל הצבה <math>x=t^{\gcd(n,m)}</math> (כאשר <math>\gcd(n,m)</math> הוא המספר הגדול ביותר עבורו <math>\frac n{\gcd(n,m)},\frac m{\gcd(n,m)}\in\mathbb Z</math>). למשל, עבור <math>\int \sqrt x(1+\sqrt[3]x)^4\mathrm dx</math> נציב <math>x=t^6</math> ונקבל <math>\int t^3\left(1+t^2\right)^4\cdot6t^5\mathrm dt</math>, שהוא אינטגרל של פולינום. | |
| − | אם <math>\frac{m+1}n\in\mathbb Z</math> אז תועיל הצבה <math>b+ax^n=t^q</math> עבור q המכנה של p. לדוגמה | + | * אם <math>\frac{m+1}n\in\mathbb Z</math> אז תועיל הצבה <math>b+ax^n=t^q</math> עבור q המכנה של p. לדוגמה, ל-<math>\int x^5\left(1+x^3\right)^\frac23\mathrm dx</math> נציב <math>1+x^3=t^3\implies x^5\mathrm dx=3t^2\frac{t^3-1}3\mathrm dt</math> ונקבל <math>\int t^2\left(3t^2\frac{t^3-1}3\right)\mathrm dt=\int\left(t^7-t^4\right)\mathrm dt=\dots</math>. |
| − | <math>\int x^5(1+x^3)^\frac23\mathrm dx</math> | + | |
===דוגמאות נוספות=== | ===דוגמאות נוספות=== | ||
| − | #<math>\int x^2\sqrt{4-x^2}\mathrm dx</math> נציב <math>x=2\sin(t)\ | + | # <math>\int x^2\sqrt{4-x^2}\mathrm dx</math> נציב <math>x=2\sin(t)\implies\mathrm dx=2\cos(t)\mathrm dt</math> ונקבל {{left|<math>\begin{align}\int&=\int4\sin^2(t)\sqrt{4-4\sin^2(t)}2\cos(t)\mathrm dt\\&=\int16\sin^2(t)\cos^2(t)\mathrm dt\\&=4\int(2\sin(t)\cos(t))^2\mathrm dt\\&=4\int\sin^2(2t)\mathrm dt\\&=4\int\frac{1-\cos(4t)}2\mathrm dt\\&=2t-\frac{\sin(4t)}2+c\\&=2\arcsin\left(\frac x2\right)-\frac{\sin\left(4\arcsin\left(\frac x2\right)\right)}2+c\end{align}</math>}} |
| − | #<math>\int\sqrt{x^2+a^2}\mathrm dx</math> עבור <math>a | + | # <math>\int\sqrt{x^2+a^2}\mathrm dx</math> עבור <math>a</math> קבוע: נציב <math>x=a\tan(\theta)\implies \mathrm dx=a\sec^2(\theta)\mathrm d\theta</math> ונקבל {{left|<math>\begin{align}\int&=\int\sqrt{a^2\tan^2(\theta)+a^2}a\sec^2(\theta)\mathrm d\theta\\&=\int a\sec(\theta)a\sec^2(\theta)\mathrm d\theta\\&=\int a^2\sec^3(\theta)\mathrm d\theta\\&=a^2\left(\frac12\sec(\theta)\tan(\theta)+\frac12\ln|\sec(\theta)+\tan(\theta)|\right)+c\\&=\frac{a^2}2\sqrt{1+\left(\frac xa\right)^2}\cdot\frac xa+\frac{a^2}2\ln\left|\sqrt{1+\left(\frac xa\right)^2}+\frac xa\right|+c\\&=\frac x2\sqrt{x^2+a^2}+\frac{a^2}2\ln\left|x+\sqrt{x^2+a^2}\right|-\underbrace{\frac{a^2}2\ln|a|+c}_\text{constant}\end{align}</math>}} |
| − | #<math>\int\sqrt{x^2-a^2}\mathrm dx</math> נציב <math>x=a\sec(\theta)</math> ונקבל <math>\int\sqrt{a^2\sec^2(\theta)-a^2}a\sec(\theta)\tan(\theta)\mathrm d\theta=\int a^2\sec(\theta)\tan^2(\theta)\ | + | # <math>\int\sqrt{x^2-a^2}\mathrm dx</math> עבור <math>a</math> קבוע: נציב <math>x=a\sec(\theta)</math> ונקבל {{left|<math>\begin{align}\int&=\int\sqrt{a^2\sec^2(\theta)-a^2}\cdot a\sec(\theta)\tan(\theta)\mathrm d\theta\\&=\int a^2\sec(\theta)\tan^2(\theta)\mathrm d\theta\\&=a^2\int \left(\sec^3(\theta)-\sec(\theta)\right)\mathrm d\theta\\&=\frac{a^2}2(\sec(\theta)\tan(\theta)+\ln|\sec(\theta)+\tan(\theta)|)-a^2\ln|\sec(\theta)+\tan(\theta)|+c\\&=\frac{a^2}2\frac xa\frac{x\sqrt{1-\left(\frac ax\right)^2}}a-\frac{a^2}2\ln\left|\frac xa+\frac{x\sqrt{1-\left(\frac ax\right)^2}}a\right|+c\\&=\frac x2\sqrt{x^2-a^2}-\frac{a^2}2\ln\left|x+\sqrt{x^2-a^2}\right|+\underbrace{\frac{a^2}2\ln|a|+c}_\text{constant}\end{align}</math>}} |
| − | =בחזרה לאינטגרל המסויים= | + | ==בחזרה לאינטגרל המסויים== |
כזכור, אם f רציפה ב-<math>[a,b]</math> אז קיימת לה פונקציה קדומה F בקטע זה, ומתקיימת נוסחת ניוטון-לייבניץ <math>\int\limits_a^b f=[F(x)]_{x=a}^b</math>. | כזכור, אם f רציפה ב-<math>[a,b]</math> אז קיימת לה פונקציה קדומה F בקטע זה, ומתקיימת נוסחת ניוטון-לייבניץ <math>\int\limits_a^b f=[F(x)]_{x=a}^b</math>. | ||
| − | ==אינטגרציה בחלקים באינטגרל המסויים== | + | ===אינטגרציה בחלקים באינטגרל המסויים=== |
כזכור מתחילים עם הזהות <math>(fg)'=f'g+fg'</math> ונקבל <math>\int\limits_a^b f'g+\int\limits_a^b fg'=[fg(x)]_{x=a}^b</math>. נעביר אגף לקבל <math>\int\limits_a^b fg=[fg(x)]_{x=a}^b-\int\limits_a^b f'g</math>. בכל אינטגרציה בחלקים באינטגרל מסויים יש שתי דרכים: | כזכור מתחילים עם הזהות <math>(fg)'=f'g+fg'</math> ונקבל <math>\int\limits_a^b f'g+\int\limits_a^b fg'=[fg(x)]_{x=a}^b</math>. נעביר אגף לקבל <math>\int\limits_a^b fg=[fg(x)]_{x=a}^b-\int\limits_a^b f'g</math>. בכל אינטגרציה בחלקים באינטגרל מסויים יש שתי דרכים: | ||
# להתעלם מהגבולות עד שנמצא פונקציה קדומה באינטגרל לא מסויים, ובסוף נחזיר את הגבול. | # להתעלם מהגבולות עד שנמצא פונקציה קדומה באינטגרל לא מסויים, ובסוף נחזיר את הגבול. | ||
| − | # להשתמש בנוסחה | + | # להשתמש בנוסחה הנ"ל. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ====דוגמאות==== | ||
| + | {{left| | ||
| + | # <math>\begin{align}\int\limits_0^\pi x\cos(x)\mathrm dx&=[x\sin(x)]_{x=0}^\pi-\int\limits_0^\pi\sin(x)\mathrm dx\\&=[x\sin(x)-\cos(x)]_{x=0}^\pi\\&=-2\end{align}</math> | ||
| + | # <math>\begin{align}\int\limits_0^1 x^{17}(1-x)^{13}\mathrm dx&=\left[\frac{(1-x)^{13}x^{18}}{18}\right]_{x=0}^1+\int\limits_0^1\frac{x^{18}}{18}13(1-x)^{12}\mathrm dx\\&=0+\frac{13}{18}\int\limits_0^1 x^{18}(1-x)^{12}\mathrm dx\\&=\frac{13}{18}\left[\frac{(1-x)^{12}x^{19}}{19}\right]_{x=0}^1+\frac{13}{18}\int\limits_0^1\frac{x^{19}}{19}12(1-x)^{11}\mathrm dx\\&=0+\frac{13\cdot12}{18\cdot19}\int\limits_0^1x^{19}(1-x)^{11}\mathrm dx\\&=\dots\\&=\frac{13\cdot12\cdot11\cdots1}{18\cdot19\cdot20\cdots30}\int\limits_0^1 x^{30}\\&=\frac{13!17!}{30!}\left[\frac{x^{31}}{31}\right]_{x=0}^1\\&=\frac1{31\binom{30}{13}}=\frac1{3\;712\;555\;350}\end{align}</math> | ||
| + | }} | ||
גם באינטגרציה ע"י הצבה באינטגרל מסויים יש שתי דרכים: | גם באינטגרציה ע"י הצבה באינטגרל מסויים יש שתי דרכים: | ||
# להתעלם מהגבולות ולפתור אינטגרל מסויים, ואח"כ להציב גבולות. | # להתעלם מהגבולות ולפתור אינטגרל מסויים, ואח"כ להציב גבולות. | ||
# להחליף את הגבולות כאשר מחליפים משתנים. נסביר זאת: | # להחליף את הגבולות כאשר מחליפים משתנים. נסביר זאת: | ||
| − | בהצבה מתחילים כלל השרשרת <math>\frac{\mathrm d}{\mathrm dx} | + | בהצבה מתחילים עם כלל השרשרת <math>\frac{\mathrm d}{\mathrm dx}F(\varphi(x))=F'(\varphi(x))\varphi'(x)=f(\varphi(x))\varphi'(x)</math> (כאשר F קדומה ל-f). לכן נציב <math>t=\varphi(x)</math> ונקבל <math>\int\limits_a^b f(\varphi(x))\varphi'(x)\mathrm dx=[F(\varphi(x))]_{x=a}^b=\int\limits_{\varphi(a)}^{\varphi(b)} f(t)\mathrm dt</math>. |
| − | + | ||
| − | + | ||
גרסה מ־22:45, 17 במרץ 2011
תוכן עניינים
שיטות אינטגרציה (המשך)
דוגמה נוספת ל-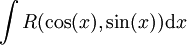 (לא עלינו):
(לא עלינו): 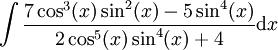
יש הצבה אוניברסלית: מציבים 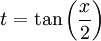 לכן
לכן 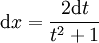 וכן
וכן 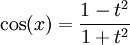 ו-
ו-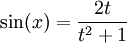 . האינטגרל הופך לאינטגרל של פונקציה רציונלית של t (שאפשר לחשב עם שברים חלקיים).
. האינטגרל הופך לאינטגרל של פונקציה רציונלית של t (שאפשר לחשב עם שברים חלקיים).
דוגמאות
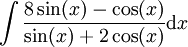 : נציב t כנ"ל ונקבל ומכאן פותרים בשברים חלקיים.
: נציב t כנ"ל ונקבל ומכאן פותרים בשברים חלקיים.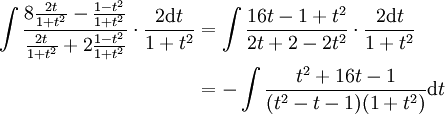
גישה יותר חכמה: מתקיים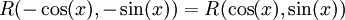 ולכן נגדיר
ולכן נגדיר 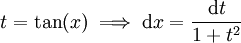 . האינטגרל הוא
. האינטגרל הוא 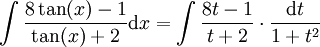 . שוב פותרים שברים חלקיים, אלא שהפעם זה יותר פשוט.
. שוב פותרים שברים חלקיים, אלא שהפעם זה יותר פשוט.-
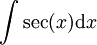 ועם
ועם 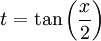 נקבל גישה אחרת:
נקבל גישה אחרת: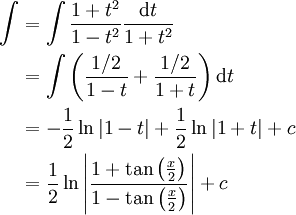
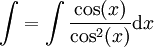 נציב
נציב 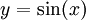 והאינטגרל הוא
והאינטגרל הוא 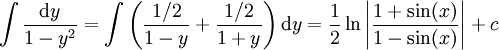 .
.
דרך המלך: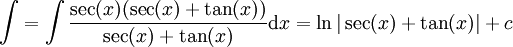 .
. -
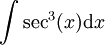 נציב
נציב 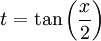 ונקבל
ונקבל 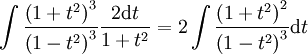 וניתן לעשות זאת, אבל זה לא נעים.
וניתן לעשות זאת, אבל זה לא נעים.
דרך אחרת: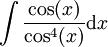 ונציב
ונציב 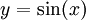 . נקבל
. נקבל 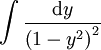 וקל לפתור זאת ע"י שברים חלקיים.
וקל לפתור זאת ע"י שברים חלקיים.
עוד דרך:נציב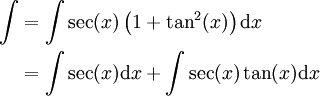
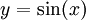 ושוב הגענו ל-
ושוב הגענו ל-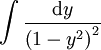 .
.
ניסיון אחרון: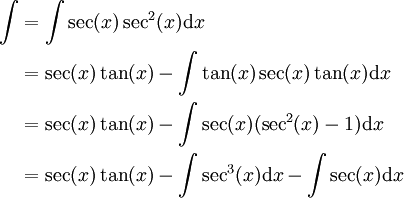
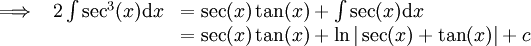
אינטגרלים עם שורשים
לאינטגרל מהסוג 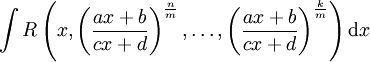 . תועיל הצבה:
. תועיל הצבה: 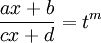
דוגמאות
-
![\int\frac{\mathrm dx}{x\left(\sqrt x+\sqrt[5]{x^2}\right)}=\int\frac{\mathrm dx}{x\left(x^\frac 5{10}+x^\frac 4{10}\right)}](/images/math/c/0/7/c07506ef53ca9089e19773c174974427.png) נציב
נציב 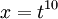 אזי נקבל
אזי נקבל 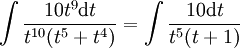 ופותרים בשברים חלקיים.
ופותרים בשברים חלקיים.
דרך אחרת: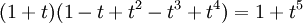 (כי
(כי 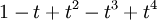 טור הנדסי). לפי זה נקבל
טור הנדסי). לפי זה נקבל 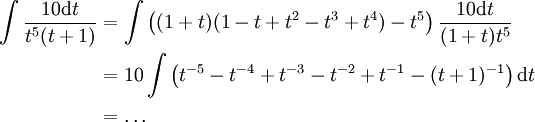
-
![\int\sqrt[3]\frac{1-x}{1+x}\frac{\mathrm dx}x](/images/math/1/1/9/1193c0ae304accbad212745a25485047.png) נציב
נציב 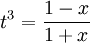 ואז
ואז 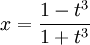 וכך
וכך 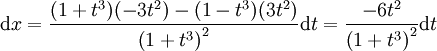 לכן
לכן 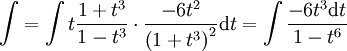 נציב
נציב 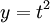 ואז
ואז 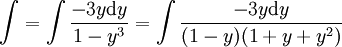 ופותרים בשברים חלקיים.
ופותרים בשברים חלקיים.
לאינטגרלים מהסוג 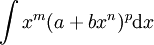 עבור
עבור 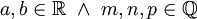 :
:
- אם
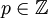 אז תועיל הצבה
אז תועיל הצבה 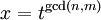 (כאשר
(כאשר 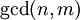 הוא המספר הגדול ביותר עבורו
הוא המספר הגדול ביותר עבורו 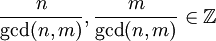 ). למשל, עבור
). למשל, עבור ![\int \sqrt x(1+\sqrt[3]x)^4\mathrm dx](/images/math/b/0/a/b0acb4c613639a4d30812ee9baad1d2e.png) נציב
נציב 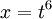 ונקבל
ונקבל 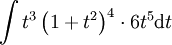 , שהוא אינטגרל של פולינום.
, שהוא אינטגרל של פולינום. - אם
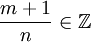 אז תועיל הצבה
אז תועיל הצבה 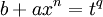 עבור q המכנה של p. לדוגמה, ל-
עבור q המכנה של p. לדוגמה, ל-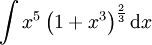 נציב
נציב 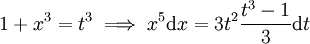 ונקבל
ונקבל 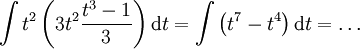 .
.
דוגמאות נוספות
-
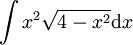 נציב
נציב 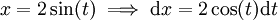 ונקבל
ונקבל 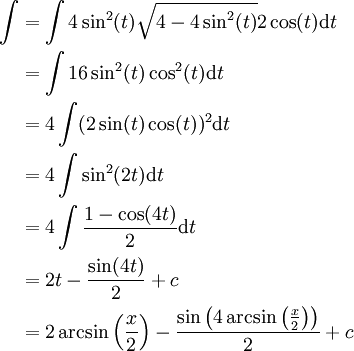
-
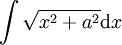 עבור
עבור  קבוע: נציב
קבוע: נציב 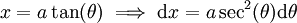 ונקבל
ונקבל 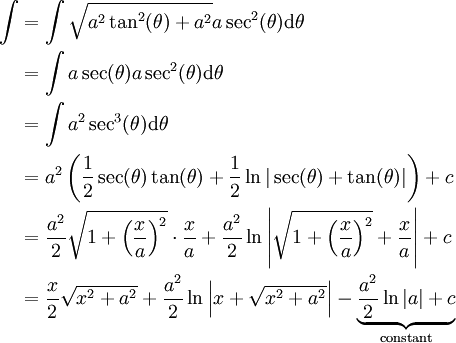
-
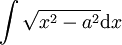 עבור
עבור  קבוע: נציב
קבוע: נציב 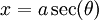 ונקבל
ונקבל 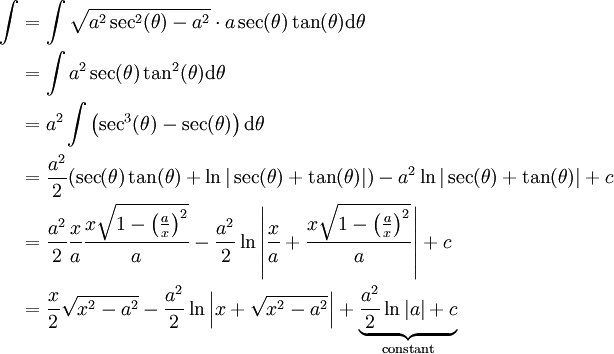
בחזרה לאינטגרל המסויים
כזכור, אם f רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז קיימת לה פונקציה קדומה F בקטע זה, ומתקיימת נוסחת ניוטון-לייבניץ
אז קיימת לה פונקציה קדומה F בקטע זה, ומתקיימת נוסחת ניוטון-לייבניץ ![\int\limits_a^b f=[F(x)]_{x=a}^b](/images/math/d/8/c/d8cac08df258c53a8179f89c2e76db6c.png) .
.
אינטגרציה בחלקים באינטגרל המסויים
כזכור מתחילים עם הזהות 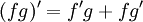 ונקבל
ונקבל ![\int\limits_a^b f'g+\int\limits_a^b fg'=[fg(x)]_{x=a}^b](/images/math/b/9/1/b91b957592b092e1185b1b91889f88e3.png) . נעביר אגף לקבל
. נעביר אגף לקבל ![\int\limits_a^b fg=[fg(x)]_{x=a}^b-\int\limits_a^b f'g](/images/math/f/6/c/f6c2d656cb9b9bd1c1debf3f12e3fec0.png) . בכל אינטגרציה בחלקים באינטגרל מסויים יש שתי דרכים:
. בכל אינטגרציה בחלקים באינטגרל מסויים יש שתי דרכים:
- להתעלם מהגבולות עד שנמצא פונקציה קדומה באינטגרל לא מסויים, ובסוף נחזיר את הגבול.
- להשתמש בנוסחה הנ"ל.
דוגמאות
גם באינטגרציה ע"י הצבה באינטגרל מסויים יש שתי דרכים:
- להתעלם מהגבולות ולפתור אינטגרל מסויים, ואח"כ להציב גבולות.
- להחליף את הגבולות כאשר מחליפים משתנים. נסביר זאת:
בהצבה מתחילים עם כלל השרשרת 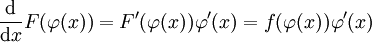 (כאשר F קדומה ל-f). לכן נציב
(כאשר F קדומה ל-f). לכן נציב 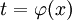 ונקבל
ונקבל ![\int\limits_a^b f(\varphi(x))\varphi'(x)\mathrm dx=[F(\varphi(x))]_{x=a}^b=\int\limits_{\varphi(a)}^{\varphi(b)} f(t)\mathrm dt](/images/math/2/1/a/21a1665c47a6b19fac01aa8c8bdea143.png) .
.
![\begin{align}\int\limits_0^\pi x\cos(x)\mathrm dx&=[x\sin(x)]_{x=0}^\pi-\int\limits_0^\pi\sin(x)\mathrm dx\\&=[x\sin(x)-\cos(x)]_{x=0}^\pi\\&=-2\end{align}](/images/math/c/7/c/c7cef2626cfbe18b5b55eac19c11fbfa.png)
![\begin{align}\int\limits_0^1 x^{17}(1-x)^{13}\mathrm dx&=\left[\frac{(1-x)^{13}x^{18}}{18}\right]_{x=0}^1+\int\limits_0^1\frac{x^{18}}{18}13(1-x)^{12}\mathrm dx\\&=0+\frac{13}{18}\int\limits_0^1 x^{18}(1-x)^{12}\mathrm dx\\&=\frac{13}{18}\left[\frac{(1-x)^{12}x^{19}}{19}\right]_{x=0}^1+\frac{13}{18}\int\limits_0^1\frac{x^{19}}{19}12(1-x)^{11}\mathrm dx\\&=0+\frac{13\cdot12}{18\cdot19}\int\limits_0^1x^{19}(1-x)^{11}\mathrm dx\\&=\dots\\&=\frac{13\cdot12\cdot11\cdots1}{18\cdot19\cdot20\cdots30}\int\limits_0^1 x^{30}\\&=\frac{13!17!}{30!}\left[\frac{x^{31}}{31}\right]_{x=0}^1\\&=\frac1{31\binom{30}{13}}=\frac1{3\;712\;555\;350}\end{align}](/images/math/b/3/9/b398631e66e50635c7a894a1400e8822.png)