הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/20.2.11"
(יצירת דף עם התוכן "בדיקה") |
|||
| שורה 1: | שורה 1: | ||
| − | + | == אינטגרציה == | |
| + | '''הגדרה שגוייה:''' אינטגרל הוא לא השטח שמתחת לגרף. למעשה, השטח שמתחת לגרף מוגדר להיות תוצאת האינטגרל (כפי שאנחנו מכירים מהחומר לבגרות). | ||
| + | |||
| + | דוגמת חישוב (ידני) של השטח: | ||
| + | |||
| + | (1) | ||
| + | |||
| + | ברור שטחי המלבנים בוודאי גדול משטח הגרף (נתעלם כרגע מהעובדה שלא הגדרנו את האינטגרל ולכן השטח לא מוגדר). | ||
| + | |||
| + | נחלק את הקטע <math>[0,1]</math>: | ||
| + | |||
| + | <math>0=x_0<x_1<x_2<\dots<x_n=1</math> | ||
| + | |||
| + | <math>x_k=k/n</math> | ||
| + | |||
| + | מעל כל תת קטע קטן <math>[x_{k-1},x_k]</math> | ||
| + | |||
| + | נבנה "מלבן חוסם" שגובהו <math>\left(k\over n\right)^2=x_k^2</math>. ביחד מלבנים אלו יוצרים שטח חוסם <math>\bar S=\sum_{k=1}^n\frac1n\left(k\over n\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3}</math> | ||
| + | |||
| + | כמו כן, מעל כל קטע קטן <math>[x_{k-1},x_k]</math> נבנה "מלבן חסום" שגובהו <math>\left(k-1\over n\right)^2=x_{k-1}^2</math> ביחד מלבנים אלה מהווים שטח חסום <math>\underline S=\frac1n\sum_{k=1}^n\left(k-1\over n\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{n(n+1)(2n+1)}{6n^3}</math> | ||
| + | |||
| + | כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-<math>\underline S\le A\le\bar S</math>. | ||
| + | |||
| + | (2) | ||
| + | |||
| + | ז"א <math>\frac{n(n+1)(2n+1)}{6n^3}\le A\le\frac{n(n+1)(2n+1)}{6n^3}</math>. | ||
| + | הדבר נכון לכל <math>n\in\mathbb N</math>. לכן נוכל להשאיף <math>n\to\infty</math> לקבל | ||
| + | <math>\frac13\le A\le\frac13</math> ולכן <math>A=\frac13</math> | ||
| + | |||
| + | === בניית האינטגרל לפי דרבו - אחר כך! === | ||
| + | |||
| + | '''הגדרה:''' תהי <math>f(x)</math> מוגדרת בקטע I. נאמר שהפונקציה <math>F(x)</math> קדומה ל-f ב-I אם <math>\forall x\in I:\ F'(x)=f(x)</math>. | ||
| + | |||
| + | ''דוגמה:'' | ||
| + | ... | ||
| + | |||
| + | '''משפט 0:''' אם <math>F(x)</math> ו-<math>G(x)</math> קדומות ל-<math>f(x)</math> בקטע I אז קיים קבוע c כך ש-<math>F(x)=G(x)+c</math> | ||
| + | |||
| + | '''הוכחה:''' נגדיר <math>H(x)=F(x)-G(x)</math> לכן <math>H'(x)=F'(x)-G'(x)</math> | ||
| + | |||
| + | .... | ||
| + | |||
| + | לפי תוצאה ממשפט לגראנג' <math>F(x)-G(x)=H(x)=c\implies F(x)=G(x)+c</math> | ||
| + | |||
| + | {{משל}} | ||
| + | |||
| + | ---- | ||
| + | '''הגדרה:''' תהי <math>f(x)\ge0</math> רציפה בקטע <math>[a,b]</math>. | ||
| + | ... | ||
| + | |||
| + | המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית): תהי <math>f(x)\ge0</math> מוגדרת ורציפה ב-<math>[a,b]</math>. לכל <math>x\in[a,b]</math> נגדיר <math>A(x)=\int\limits_a^x f(t)dt</math> אזי <math>f(x)=A'(x)</math> לכל <math>x\in[a,b]</math>. | ||
| + | |||
| + | 2) אם <math>F(x)</math> קדומה ל-<math>f(x)</math> ב-<math>[a,b]</math> אז <math>\int\limits_a^bf(t)dt=F(b)-F(a)</math>. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''הוכחה:''' (א) (3) | ||
| + | רואים <math>A(a)=0</math> | ||
| + | המטרה <math>A(b)=\int\limits_a^bf(t)dt</math>. | ||
| + | |||
| + | <math>A(x)</math> עולה | ||
| + | |||
| + | כעת לפי ההגדרה <math>A'(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math> | ||
| + | |||
| + | בציור <math>A(x+\Delta x}-A(x)</math> = השטח הארובה | ||
| + | <math>\Delta x</math> = בסיס הארובה | ||
| + | לכן <math>\frac{A(x+\Delta x)-A(x)}{\Delta x}</math> = הגובה הממוצע של הארובה. | ||
| + | |||
| + | כאשר <math>\Delta x\to0</math> זה שואף ל-<math>f(x)</math> שהיא <math>A(x)</math>. | ||
| + | |||
| + | (ב) נתונה פונקציה קדומה <math>F(x)</math> אבל מחלק א ידוע שגם <math>A(x)</math> פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-<math>F(x)=A(x)+c</math> | ||
| + | |||
| + | לכן <math>F(b)-F(a)=A(b)+c-\underbrace{(A(a)+c)}{=0}=A(b)=\int\limits_a^bf(x)dx</math> | ||
| + | |||
| + | === הגישה של דרבו === | ||
| + | תהי <math>f(x)</math> מוגדרת וחסומה <math>m\le F(x)\le M</math> בקטע <math>[a,b]</math>. נגדיר את התנודה של f ע"י <math>\Omega=M-m</math>. כעת נגדיר חלוקה P של <math>[a,b]</math> | ||
| + | |||
| + | <math>a=x_0<x_1<\dots<x_n=b</math> | ||
גרסה מ־14:19, 20 בפברואר 2011
אינטגרציה
הגדרה שגוייה: אינטגרל הוא לא השטח שמתחת לגרף. למעשה, השטח שמתחת לגרף מוגדר להיות תוצאת האינטגרל (כפי שאנחנו מכירים מהחומר לבגרות).
דוגמת חישוב (ידני) של השטח:
(1)
ברור שטחי המלבנים בוודאי גדול משטח הגרף (נתעלם כרגע מהעובדה שלא הגדרנו את האינטגרל ולכן השטח לא מוגדר).
נחלק את הקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
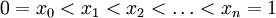
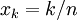
מעל כל תת קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png)
נבנה "מלבן חוסם" שגובהו עיבוד הנוסחה נכשל (שגיאת תחביר): \left(k\over n\right)^2=x_k^2 . ביחד מלבנים אלו יוצרים שטח חוסם עיבוד הנוסחה נכשל (שגיאת תחביר): \bar S=\sum_{k=1}^n\frac1n\left(k\over n\right)^2=\frac1{n^3}\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6n^3}
כמו כן, מעל כל קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) נבנה "מלבן חסום" שגובהו עיבוד הנוסחה נכשל (שגיאת תחביר): \left(k-1\over n\right)^2=x_{k-1}^2
נבנה "מלבן חסום" שגובהו עיבוד הנוסחה נכשל (שגיאת תחביר): \left(k-1\over n\right)^2=x_{k-1}^2
ביחד מלבנים אלה מהווים שטח חסום עיבוד הנוסחה נכשל (שגיאת תחביר): \underline S=\frac1n\sum_{k=1}^n\left(k-1\over n\right)^2=\frac1{n^3}\sum_{k=1}^n(k-1)^2=\frac1{n^3}\sum_{k=1}^{n-1}k^2=\frac{n(n+1)(2n+1)}{6n^3}
כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-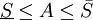 .
.
(2)
ז"א 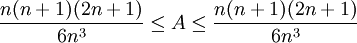 .
הדבר נכון לכל
.
הדבר נכון לכל 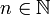 . לכן נוכל להשאיף
. לכן נוכל להשאיף 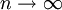 לקבל
לקבל
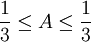 ולכן
ולכן 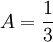
בניית האינטגרל לפי דרבו - אחר כך!
הגדרה: תהי  מוגדרת בקטע I. נאמר שהפונקציה
מוגדרת בקטע I. נאמר שהפונקציה 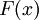 קדומה ל-f ב-I אם
קדומה ל-f ב-I אם 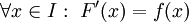 .
.
דוגמה: ...
משפט 0: אם 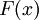 ו-
ו-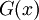 קדומות ל-
קדומות ל- בקטע I אז קיים קבוע c כך ש-
בקטע I אז קיים קבוע c כך ש-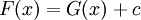
הוכחה: נגדיר 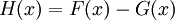 לכן
לכן 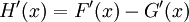
....
לפי תוצאה ממשפט לגראנג' 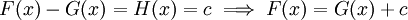

הגדרה: תהי 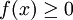 רציפה בקטע
רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
...
.
...
המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית): תהי 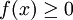 מוגדרת ורציפה ב-
מוגדרת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . לכל
. לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) נגדיר
נגדיר 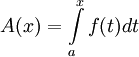 אזי
אזי 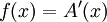 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) .
.
2) אם 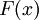 קדומה ל-
קדומה ל- ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 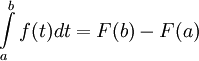 .
.
הוכחה: (א) (3)
רואים 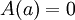 המטרה
המטרה 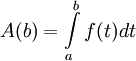 .
.
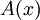 עולה
עולה
כעת לפי ההגדרה 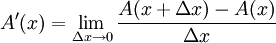
בציור עיבוד הנוסחה נכשל (שגיאת תחביר): A(x+\Delta x}-A(x)
= השטח הארובה
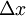 = בסיס הארובה
לכן
= בסיס הארובה
לכן 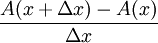 = הגובה הממוצע של הארובה.
= הגובה הממוצע של הארובה.
כאשר 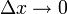 זה שואף ל-
זה שואף ל- שהיא
שהיא 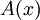 .
.
(ב) נתונה פונקציה קדומה 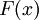 אבל מחלק א ידוע שגם
אבל מחלק א ידוע שגם 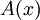 פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-
פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-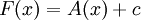
לכן 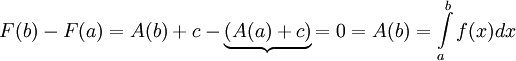
הגישה של דרבו
תהי  מוגדרת וחסומה
מוגדרת וחסומה 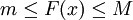 בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר את התנודה של f ע"י
. נגדיר את התנודה של f ע"י 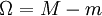 . כעת נגדיר חלוקה P של
. כעת נגדיר חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)