הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/20.2.11"
(אין הבדלים)
| |
גרסה מ־17:07, 20 בפברואר 2011
תוכן עניינים
אינטגרציה
הגדרה שגוייה: אינטגרל הוא לא השטח שמתחת לגרף. למעשה, השטח שמתחת לגרף מוגדר להיות תוצאת האינטגרל (כפי שאנחנו מכירים מהחומר לבגרות).
דוגמת חישוב (ידני) של השטח:
(1)
ברור שטחי המלבנים בוודאי גדול משטח הגרף (נתעלם כרגע מהעובדה שלא הגדרנו את האינטגרל ולכן השטח לא מוגדר).
נחלק את הקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
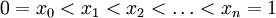
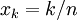
מעל כל תת קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png)
נבנה "מלבן חוסם" שגובהו 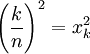 . ביחד מלבנים אלו יוצרים שטח חוסם
. ביחד מלבנים אלו יוצרים שטח חוסם 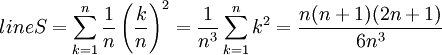
כמו כן, מעל כל קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) נבנה "מלבן חסום" שגובהו
נבנה "מלבן חסום" שגובהו 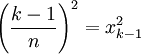 ביחד מלבנים אלה מהווים שטח חסום
ביחד מלבנים אלה מהווים שטח חסום 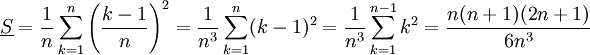
כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-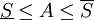 .
.
(2)
ז"א 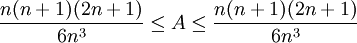 .
הדבר נכון לכל
.
הדבר נכון לכל 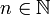 . לכן נוכל להשאיף
. לכן נוכל להשאיף 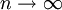 לקבל
לקבל
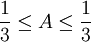 ולכן
ולכן 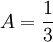
בניית האינטגרל לפי דרבו - אחר כך
הגדרה: תהי  מוגדרת בקטע I. נאמר שהפונקציה
מוגדרת בקטע I. נאמר שהפונקציה 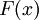 קדומה ל-f ב-I אם
קדומה ל-f ב-I אם 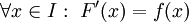 .
.
דוגמה: ...
משפט 0: אם 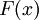 ו-
ו-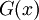 קדומות ל-
קדומות ל- בקטע I אז קיים קבוע c כך ש-
בקטע I אז קיים קבוע c כך ש-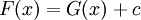
הוכחה: נגדיר 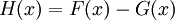 לכן
לכן 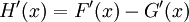
....
לפי תוצאה ממשפט לגראנג' 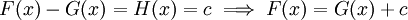

הגדרה: תהי 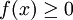 רציפה בקטע
רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
...
.
...
המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית): תהי 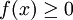 מוגדרת ורציפה ב-
מוגדרת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . לכל
. לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) נגדיר
נגדיר 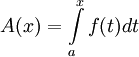 אזי
אזי 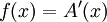 לכל
לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) .
.
2) אם 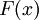 קדומה ל-
קדומה ל- ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 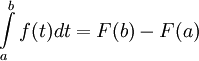 .
.
הוכחה: (א) (3)
רואים 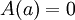 המטרה
המטרה 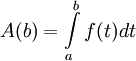 .
.
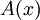 עולה
עולה
כעת לפי ההגדרה 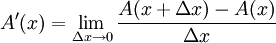
בציור 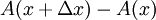 = השטח הארובה
= השטח הארובה
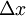 = בסיס הארובה
לכן
= בסיס הארובה
לכן 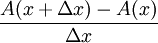 = הגובה הממוצע של הארובה.
= הגובה הממוצע של הארובה.
כאשר 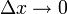 זה שואף ל-
זה שואף ל- שהיא
שהיא 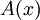 .
.
(ב) נתונה פונקציה קדומה 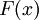 אבל מחלק א ידוע שגם
אבל מחלק א ידוע שגם 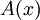 פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-
פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-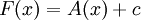
לכן 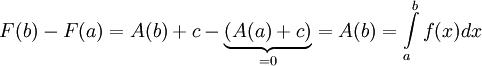
הגישה של דרבו
תהי  מוגדרת וחסומה
מוגדרת וחסומה 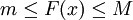 בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר את התנודה של f ע"י
. נגדיר את התנודה של f ע"י 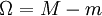 . כעת נגדיר חלוקה P של
. כעת נגדיר חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
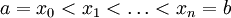
עוד נגדיר לכל  אורך תת קטע מספר k =
אורך תת קטע מספר k = 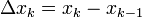
והפרמטר של P, 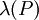 מוגדר ע"י
מוגדר ע"י 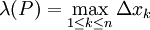
לכל k, 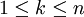 נגדיר
נגדיר
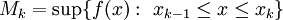 וכן
וכן 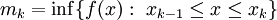 .
.
(4)
בהתאם לכך נגדיר "שטח חוסם"
0הסכום העליון
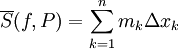 ושטח חסום תחתון
ושטח חסום תחתון
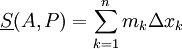
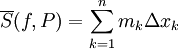
משפט 1: עבור כל חלוקה P
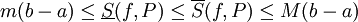
הוכחה: 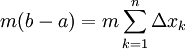 (כי
(כי 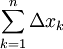 = סכום כל הרווחים בין n נקודות החלוקה = b-a)
= סכום כל הרווחים בין n נקודות החלוקה = b-a)
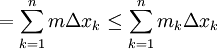 (כי לכל k מתקיים
(כי לכל k מתקיים 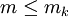 )
)
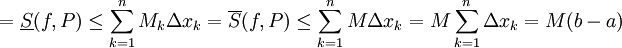
לפי משפט 1 המספרים 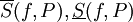 חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
לכן מוגדרים היטב ה"אינטגרל העליון" עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \overline\int\limits_a^b f(x)dx=\inf_P \overline S(f,P)
ו"האינטגרל התחתון" עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \underline\int\limits_a^b f(x)dx=\sup_P \underline S(f,P)
.
הגדרת האינטגרל לפי דרבו
תהי f(x) מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נאמר ש-f אינטגרבילית (דרבו) ב-
נאמר ש-f אינטגרבילית (דרבו) ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \underline\int\limits_a^b f(x)dx=\overline\int\limits_a^b f(x)dx
אם עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \underline\int\limits_a^b f(x)dx=\overline\int\limits_a^b f(x)dx
ואם הם שווים אז נגדירלהיות הערך המשותף של
ו-עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \overline\int f
.
דוגמהף בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כלהו נגדיר את פונקצית דיריכלה
כלהו נגדיר את פונקצית דיריכלה 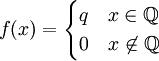 .
נקח חלוקה כלשהי ל-
.
נקח חלוקה כלשהי ל-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
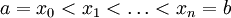 לכל k
לכל k
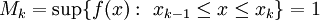 וכן
וכן 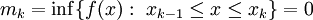
לכן עיבוד הנוסחה נכשל (שגיאת תחביר): \overline S(f,P)=\sum_{k=1}^n M_k\Delta x_k=\sum_{k=1)^n 1\Delta x_k=b-a
ואילו עיבוד הנוסחה נכשל (שגיאת תחביר): \underline S(f,P)=\sum_{k=1}^n m_k\Delta x_k=\sum_{k=1)^n 0\Delta x_k=0
.
מכאן עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \underline\int\limits_a^b f(x)dx=\sup_P \underline S(f,P)=0
ו-עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \overline\int\limits_a^b f(x)dx=\inf_P \overline S(f,P)=b-a
. הם לא שווים ולכן f לא אינטגרבילית.
הגדרה: תהי P חלוקה של קטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . חלוקה Q של
. חלוקה Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
משפט 2: תהי  מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . תהי P חלוקה של
. תהי P חלוקה של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-Q עידון של P ע"י הוספת r נקודות. אז
ו-Q עידון של P ע"י הוספת r נקודות. אז
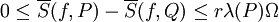
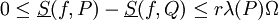
(כאשר 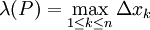 ו-
ו-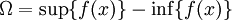 )
)
ז"א הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-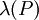
הוכחה: מקרה ראשון: 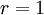 . ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת
. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת 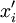 . כך ש-
. כך ש-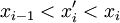 . בהתאם לכך נגדיר
. בהתאם לכך נגדיר 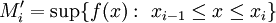 ו-
ו-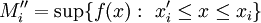 כעת בכל תת קטע
כעת בכל תת קטע ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) מתקיים
מתקיים 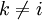 . לא שינינו כלום.
לכן
. לא שינינו כלום.
לכן 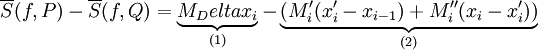
- תרומת קטע i ל-
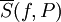
- תרומת קטע i ל-
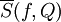
לפי עצם ההגדרות 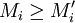 ו-
ו-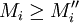 לכן
לכן