הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/20.2.11"
(←הוכחה) |
(←הוכחה) |
||
| שורה 128: | שורה 128: | ||
לפי ההגדרות <math>M_i\ge M_i^+,M_i^-</math> ולפיכך {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align}</math>}} | לפי ההגדרות <math>M_i\ge M_i^+,M_i^-</math> ולפיכך {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\ge M_i\Delta x_i-\Big(M_i(x_i'-x_{i-1})+M_i(x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i'-x_{i-1}+x_i-x_i')\Big)\\&=M_i\Big(\Delta x_i-(x_i-x_{i-1})\Big)\\&=0\end{align}</math>}} | ||
| − | {{הערה|את ההמשך עשינו ב[[משתמש:אור שחף/133 - הרצאה/22.2.11|הרצאה | + | {{הערה|את ההמשך עשינו ב[[משתמש:אור שחף/133 - הרצאה/22.2.11|הרצאה שאחריה]]:}} |
| − | כמו כן, <math>\overline S(f,P)-\overline S(f,Q)\le | + | כמו כן, |
| + | {{left|<math>\begin{align}\overline S(f,P)-\overline S(f,Q)&\le M_i(x_i-x_{i-1})-m_i(x_i-x_{i-1})\\&=(M_i-m_i)(x_i-x_{i-1})\\&\le\Omega(x_i-x_{i-1})\\&\le\underbrace{r}_{=1}\lambda(P)\Omega\end{align}</math>}} | ||
| − | מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר <math>\Omega\lambda(P)</math>. לכן מיד נסיק <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P)</math>. | + | מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר <math>\Omega\lambda(P)</math> בכל אחת מ-r המפעמים. לכן מיד נסיק <math>0\le\overline S(f,P)-\overline S(f,Q)\le r\Omega\lambda(P)</math>. |
ההוכחה לסכום תחתון דומה. {{משל}} | ההוכחה לסכום תחתון דומה. {{משל}} | ||
| + | |||
| + | ===מסקנה 1=== | ||
| + | נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של <math>[a,b]</math>. אזי <math>\underline S(f,P)\le\overline S(f,Q)</math>. | ||
| + | ====הוכחה==== | ||
| + | נבנה עידון משותף, ז"א <math>R=P\cup Q</math>. לפי משפט 2 מתקיים <math>\underline S(f,P)\le\underline S(f,R)\le \overline S(f,R)\le\overline S(f,Q)</math>. {{משל}} | ||
| + | |||
| + | ===מסקנה 2=== | ||
| + | עבור f כנ"ל מתקיים <math>\underline\int_a^b f(x)dx\le\overline{\int}_a^b f(x)dx</math>. | ||
| + | ====הוכחה==== | ||
| + | מסקנה 1 אומרת שלכ שתי חלוקות P,Q של <math>[a,b]</math> מתקיים <math>\underline S(f,P)\le\overline S(f,Q)</math> ולכן <math>\sup_P\underline S(f,P)\le\inf_Q\overline S(f,Q)</math>. כמו כן, לפי ההגדרה <math>\underline\int_a^b f(x)dx=\sup_Q\underline S(f,Q)</math> ו-<math>\inf_P\overline S(f,P)=\overline{\int}_a^b f(x)dx</math>. {{משל}} | ||
גרסה מ־12:33, 23 בפברואר 2011
תוכן עניינים
אינטגרציה
הגדרה שגוייה: אינטגרל הוא לא השטח שמתחת לגרף. עם זאת, האינטגרל נותן אינדיקציה טובה לשטח זה.
דוגמת חישוב (ידני) של שטח שמתחת לגרף
נתון הגרף (1). נחשב את השטח שמתחת לו. לצורך כך נחשב תחילה את השטח של המלבנים הגדולים והמלבנים הקטנים (החוסמים והחסומים).
ברור שסכום שטחי המלבנים גדול משטח הגרף. נחלק את הקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) :
:
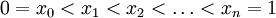
(באופן כללי 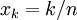 )
)
מעל כל תת קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) נבנה "מלבן חוסם" שגובהו
נבנה "מלבן חוסם" שגובהו 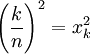 . ביחד מלבנים אלו יוצרים שטח חוסם
. ביחד מלבנים אלו יוצרים שטח חוסם 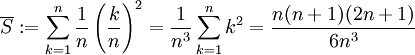
כמו כן, מעל כל קטע קטן ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) נבנה "מלבן חסום" שגובהו
נבנה "מלבן חסום" שגובהו 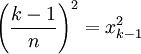 ביחד מלבנים אלה מהווים שטח חסום
ביחד מלבנים אלה מהווים שטח חסום 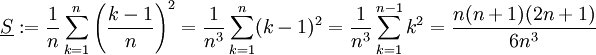
כעת אם A מציין את השטח שמתחת לגרף בוודאי ש-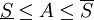 , ז"א
, ז"א 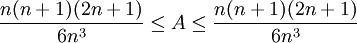 . הדבר נכון לכל
. הדבר נכון לכל 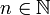 ולכן נוכל להשאיף את
ולכן נוכל להשאיף את 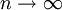 ולקבל
ולקבל
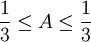 , לכן
, לכן 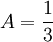 .
. 
הגדרה: תהי 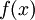 מוגדרת בקטע I. נאמר שהפונקציה
מוגדרת בקטע I. נאמר שהפונקציה 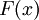 קדומה ל-f ב-I אם
קדומה ל-f ב-I אם 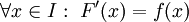 .
.
דוגמה: אם 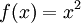 אז
אז 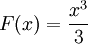 .
.
משפט 0
אם 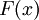 ו-
ו-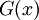 קדומות ל-
קדומות ל-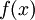 בקטע I אז קיים קבוע c כך ש-
בקטע I אז קיים קבוע c כך ש-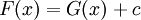
הוכחה
נגדיר 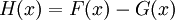 ולכן
ולכן 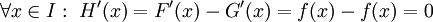 . לפי תוצאה ממשפט לגרנג'
. לפי תוצאה ממשפט לגרנג' 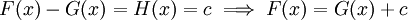 .
. 
הגדרה: תהי 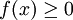 רציפה בקטע
רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נסמן ב-
. נסמן ב-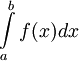 את השטח שמתחת לגרף.
את השטח שמתחת לגרף.
המשפט היסודי של חשבון אינטגרלי (בצורה אינטואיטיבית)
תהי 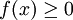 מוגדרת ורציפה ב-
מוגדרת ורציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
- לכל
![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) נגדיר
נגדיר 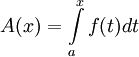 אזי
אזי ![\forall x\in[a,b]:\ f(x)=A'(x)](/images/math/1/3/7/13710ea0bb86814758afa8b4f8e1b17a.png) .
. - אם
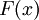 קדומה ל-
קדומה ל-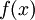 ב-
ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז 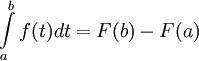 .
.
הוכחה
- גרף (3). רואים ש-
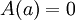 וננסה להוכיח ש-
וננסה להוכיח ש-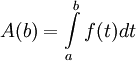 .
יהי x נתון. כעת לפי ההגדרה
.
יהי x נתון. כעת לפי ההגדרה 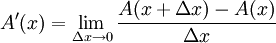 . בציור:
. בציור: 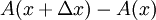 = שטח הארובה,
= שטח הארובה, 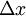 = בסיס הארובה, לכן
= בסיס הארובה, לכן 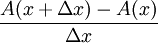 = הגובה הממוצע של הארובה.
לכן
= הגובה הממוצע של הארובה.
לכן 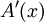 = הגובה הממוצע כאשר
= הגובה הממוצע כאשר 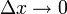 =
=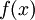 .
. 
- נתונה פונקציה קדומה
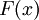 . מחלק 1 ידוע גם ש-
. מחלק 1 ידוע גם ש-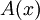 פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-
פונקציה קדומה. לפי משפט 0 יש קבוע c כך ש-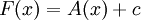 . לכן
. לכן 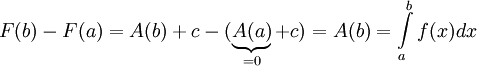 .
. 
האינטגרל לפי דרבו
הקדמה - הגדרות
תהי 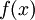 מוגדרת וחסומה ע"י
מוגדרת וחסומה ע"י 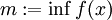 ו-
ו- 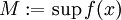 בקטע
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נגדיר את התנודה של f ע"י
. נגדיר את התנודה של f ע"י 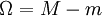 . כעת נגדיר חלוקה P של
. כעת נגדיר חלוקה P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
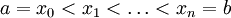
עוד נגדיר לכל 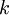 את אורך תת קטע מספר k להיות
את אורך תת קטע מספר k להיות 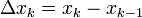 ואת הפרמטר של P להיות
ואת הפרמטר של P להיות 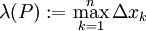 .
.
לכל k כך ש-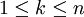 נגדיר
נגדיר
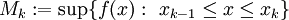 וכן
וכן 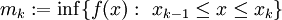 .
.
גרף (4).
בהתאם לכך נגדיר:
- שטח חוסם - הסכום העליון:
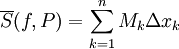
- שטח חסום - הסכום התחתון:
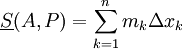
משפט 1
בסימונים הנ"ל, עבור כל חלוקה P מתקיים 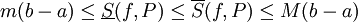 .
.
הוכחה
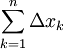 = סכום כל הרווחים בין n נקודות החלוקה = b-a = סכום כל הרווחים בין n נקודות החלוקה = b-a
|
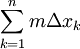
|

|
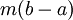
|
|||
לכל k מתקיים 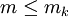 . .
|
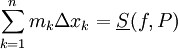
|
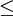
|
||||
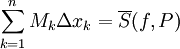
|
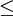
|
|||||
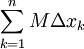
|
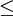
|
|||||
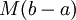
|

|

נשים לב כי לפי משפט 1 המספרים 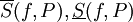 חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
חסומים מלעיל ומלרע באופן ב"ת (בלתי תלוי) ב-P (אבל בוודאי תלוי ב-f).
לכן מוגדרים היטב ה"אינטגרל העליון" 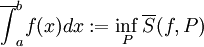 ו"האינטגרל התחתון"
ו"האינטגרל התחתון" 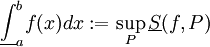 .
.
הגדרת האינטגרל לפי דרבו
תהי 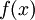 מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נאמר ש-f אינטגרבילית לפי דרבו ב-
. נאמר ש-f אינטגרבילית לפי דרבו ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אם
אם 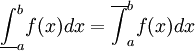 ואם הם שווים אז נגדיר
ואם הם שווים אז נגדיר 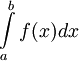 להיות הערך המשותף של
להיות הערך המשותף של 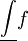 ו-
ו-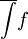 .
.
דוגמה
בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כלשהו נגדיר את פונקצית דיריכלה
כלשהו נגדיר את פונקצית דיריכלה 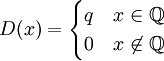 .
נקח חלוקה כלשהי ל-
.
נקח חלוקה כלשהי ל-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: 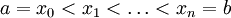 .
.
לכל k מתקיים 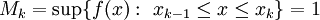 וכן
וכן 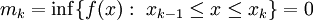 . לכן
. לכן 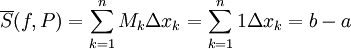 ואילו
ואילו 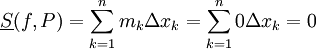 .
.
מכאן 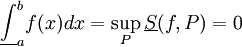 ו-
ו-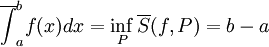 . הם לא שווים ולכן f לא אינטגרבילית.
. הם לא שווים ולכן f לא אינטגרבילית. 
הגדרה: תהי P חלוקה של קטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . חלוקה Q של
. חלוקה Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
נקראת עידון או העדנה של P אם Q מכילה את כל נקודות החלוקה של P ועוד נקודות.
משפט 2
תהי 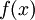 מוגדרת וחסומה ב-
מוגדרת וחסומה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . תהי P חלוקה של
. תהי P חלוקה של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ו-Q עידון של P ע"י הוספת r נקודות. אז
ו-Q עידון של P ע"י הוספת r נקודות. אז
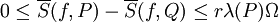
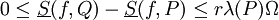
(נזכיר ש-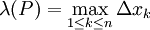 ו-
ו-![\Omega=\sup_{x\in[a,b]} f(x)-\inf_{x\in[a,b]} f(x)](/images/math/2/4/1/2419d29a1233ecbb399ae08750e1ce1e.png) )
)
כלומר, הסכום העליון יורד והסכום התחתון עולה ע"י עידון אבל השינוי בהם קטן מ-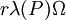 .
.
הוכחה
מקרה ראשון: 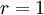 . ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת
. ז"א Q מתקבלת מ-P ע"י הוספת נקודה אחת 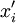 כך ש-
כך ש-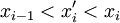 עבור i כלשהו. בהתאם לכך נגדיר
עבור i כלשהו. בהתאם לכך נגדיר 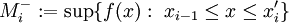 ו-
ו-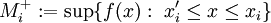 .
כמו כן, לא שינינו כל תת קטע
.
כמו כן, לא שינינו כל תת קטע ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) עבור
עבור 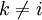 כלשהו. לכן
כלשהו. לכן 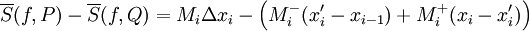
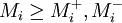 ולפיכך
ולפיכך 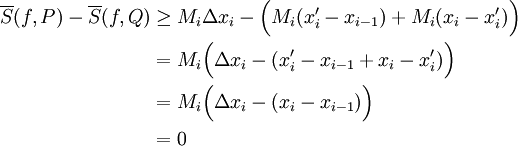
את ההמשך עשינו בהרצאה שאחריה:
כמו כן,
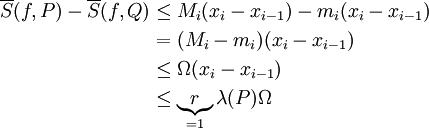
מקרה כללי: Q מתקבלת מ-P ע"י הוספת r נקודות. נוסיף אותן אחת אחת. הסכום העליון יורד, אבל לא יותר מאשר 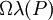 בכל אחת מ-r המפעמים. לכן מיד נסיק
בכל אחת מ-r המפעמים. לכן מיד נסיק 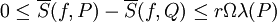 .
.
ההוכחה לסכום תחתון דומה. 
מסקנה 1
נקח f כנ"ל ונניח ש-P ו-Q הן שתי חלוקות כלשהן של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . אזי
. אזי 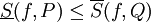 .
.
הוכחה
נבנה עידון משותף, ז"א 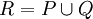 . לפי משפט 2 מתקיים
. לפי משפט 2 מתקיים 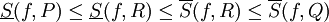 .
. 
מסקנה 2
עבור f כנ"ל מתקיים 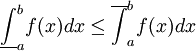 .
.
הוכחה
מסקנה 1 אומרת שלכ שתי חלוקות P,Q של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים
מתקיים 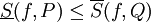 ולכן
ולכן 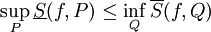 . כמו כן, לפי ההגדרה
. כמו כן, לפי ההגדרה 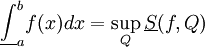 ו-
ו-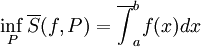 .
. 