משתמש:אור שחף/133 - הרצאה/3.5.11
את רשימת המשפטים לאינטגרלים לא אמיתיים מסוג II לא סיימנו בהרצאה הקודמת ולכן השלמנו אותו ב-3.5.11. חלק זה מופיע בסיכום ההרצאה הקודמת ולא בדף הנוכחי.
אינטגרל לא אמיתי, סוג II (המשך)
דוגמה
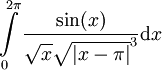 - מתכנס או מתבדר?
- מתכנס או מתבדר?
נסמן 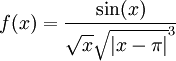 . לפונקציה יש נקודת אי רציפות סליקה באפס כי
. לפונקציה יש נקודת אי רציפות סליקה באפס כי 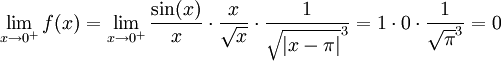 . כמו כן יש סינגולריות רק ב-
. כמו כן יש סינגולריות רק ב-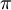 ונרשום:
ונרשום: 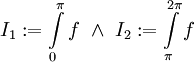 .
.
f אי-שלילית בקטע ![[0,\pi]](/images/math/e/1/8/e1868564b62b4e2f1c063321df289469.png) . לכן נגדיר
. לכן נגדיר 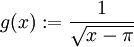 ונחשב
ונחשב 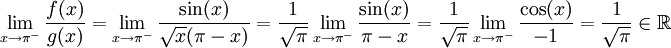 ולכן
ולכן 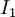 מתכנס אם
מתכנס אם 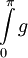 מתכנס, מה שאכן מתקיים:
מתכנס, מה שאכן מתקיים: ![\int\limits_0^\pi g=\int\limits_0^\pi(\pi-x)^{-1/2}\mathrm dx=\left[-2\sqrt{\pi-x}\right]_{x=0}^\pi=2\sqrt\pi](/images/math/3/7/4/374029fe4970b1abb0ecde4e5723cc60.png) . באותו אופן אפשר להוכיח התכנסות
. באותו אופן אפשר להוכיח התכנסות 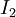 (השוואה עם
(השוואה עם 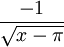 ). מכאן שאינטגרל הנתון מתכנס.
). מכאן שאינטגרל הנתון מתכנס. 
נושא שני:
סדרות וטורים של פונקציות
הגדרה: תהי 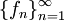 סדרת פונקציות המוגדרות כולן בקטע
סדרת פונקציות המוגדרות כולן בקטע 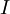 . לכל
. לכל 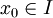 נקבל סדרת מספרים
נקבל סדרת מספרים 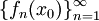 ואפשר לדון ב-
ואפשר לדון ב-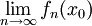 . נגדיר את "תחום ההתכנסות"
. נגדיר את "תחום ההתכנסות" 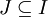 של הסדרה כ-
של הסדרה כ-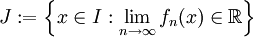 . כמו כן מוגדרת "פונקציה גבולית"
. כמו כן מוגדרת "פונקציה גבולית" 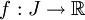 כך ש-
כך ש-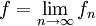 .
.
יש 2 נקודות מבט בהן ניתן להסתכל על סדרת פונקציות:
- סדרת פונקציות
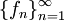 היא פשוט אינסוף סדרות של מספרים
היא פשוט אינסוף סדרות של מספרים 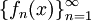 , עם
, עם 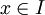 לכל סדרה. זהו מבט נקודתי.
לכל סדרה. זהו מבט נקודתי. - סדרת פונקציות היא, כשמה, סדרה של פונקציות ששואפות לפונקציה חדשה - הפונקציה הגבולית. זהו מבט פונקציונלי.
הגדרה: נניח שיש לנו סדרת פונקציות 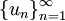 על I. אפשר לבנות טור
על I. אפשר לבנות טור 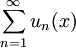 כאשר התכנסות הטור נקבעת עפ"י הסכומים החלקיים
כאשר התכנסות הטור נקבעת עפ"י הסכומים החלקיים 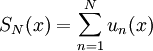 וה-
וה-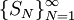 סדרת פונקציות על I. תחום ההתכנסות ל-
סדרת פונקציות על I. תחום ההתכנסות ל-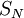 , לפי ההגדרה,
, לפי ההגדרה, 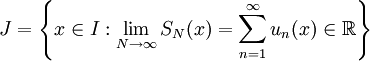 . כמו כן הפונקציה הגבולית של הסדרה היא
. כמו כן הפונקציה הגבולית של הסדרה היא 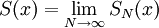 .
.
דוגמאות
-
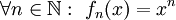 . זאת סדרת פונקציות על
. זאת סדרת פונקציות על 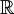 ומתקיים
ומתקיים 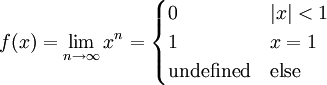 . לפיכך תחום ההתכנסות הוא הקטע
. לפיכך תחום ההתכנסות הוא הקטע ![J=(-1,1]](/images/math/b/6/0/b604e8a4aaf52c7e068790f5319abbee.png) . נשים לב כי יש לפונקציה הגבולית נקודת אי-רציפות ב-
. נשים לב כי יש לפונקציה הגבולית נקודת אי-רציפות ב-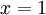 אעפ"י שכל ה-
אעפ"י שכל ה-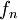 רציפות בנקודה זו.
רציפות בנקודה זו. - נחשב את הפונקציה הגבולית עבור
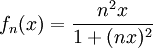 . עבור
. עבור 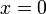 מתקיים
מתקיים 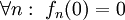 . עבור
. עבור 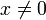 נקבל
נקבל 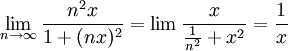 . לכן הפונקציה הגבולית היא
. לכן הפונקציה הגבולית היא 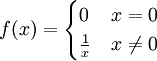 .
. - הטור הנדסי
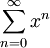 שווה ל-
שווה ל-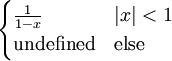 . תחום ההתכנסות הוא
. תחום ההתכנסות הוא 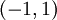 .
. - נבדוק למה שווה הטור
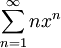 עבור
עבור 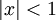 :
: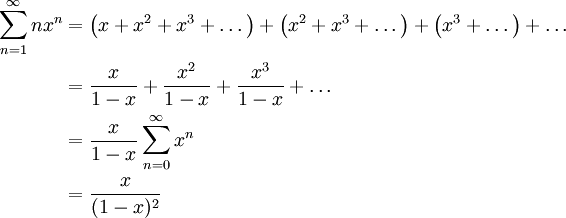

גישה אחרת (מבט פונקציונלי): נגדיר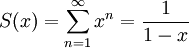 . אם יש צדק בעולם
. אם יש צדק בעולם 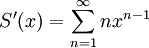 ולכן
ולכן 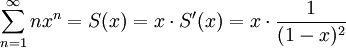 , אלא שאנו זקוקים למשפט כדי להצדיק את גזירת הטור איבר-איבר אינסוף פעמים (כלומר משפט האומר ש-
, אלא שאנו זקוקים למשפט כדי להצדיק את גזירת הטור איבר-איבר אינסוף פעמים (כלומר משפט האומר ש-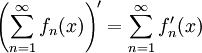 ), ועוד לא הוכחנו כזה דבר (אך נעיר שזה נכון).
), ועוד לא הוכחנו כזה דבר (אך נעיר שזה נכון). - נגדיר
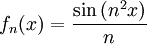 . לכן הפונקציה הגבולית היא
. לכן הפונקציה הגבולית היא 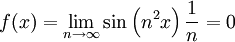 . אם יש צדק בעולם אז
. אם יש צדק בעולם אז 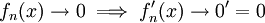 , אלא שצדק נמצא בחלל ובפרט
, אלא שצדק נמצא בחלל ובפרט 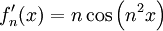 ולכן
ולכן 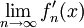 לא קיים לאף
לא קיים לאף 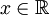 .
. - נתבונן בטור
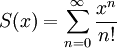 ונוכיח כי
ונוכיח כי 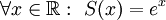 . נעשה זאת באמצעות טורי טיילור:
. נעשה זאת באמצעות טורי טיילור: 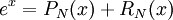 וכבר הראנו בקורס אינפי 1 ש-
וכבר הראנו בקורס אינפי 1 ש-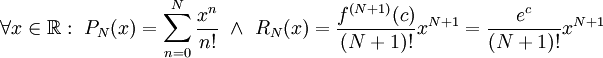 עבור c כלשהו בין 0 ל-x. כעת הטור הנתון מקיים
עבור c כלשהו בין 0 ל-x. כעת הטור הנתון מקיים 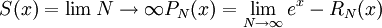 . כדי להראות ש-
. כדי להראות ש-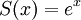 נותר להוכיח ש-
נותר להוכיח ש-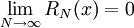 . ובכן נקח
. ובכן נקח 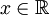 כרצונינו ונשים לב כי
כרצונינו ונשים לב כי 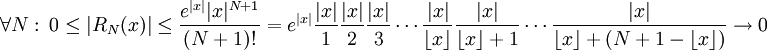
וכך הוכחנו בעזרת המבט הנקודתי. עתה ננסה להוכיח גם מנקודת מבט פונקציונלית:
עתה ננסה להוכיח גם מנקודת מבט פונקציונלית: 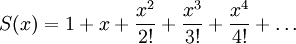 ולכן
ולכן 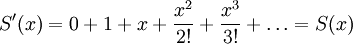 . נגדיר
. נגדיר 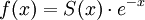 ולכן
ולכן 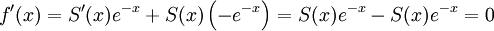 ומכאן ש-f פונקציה קבועה. נסמן
ומכאן ש-f פונקציה קבועה. נסמן 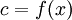 ונובע ש-
ונובע ש-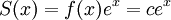 . מהגדרת S נובע כי
. מהגדרת S נובע כי 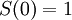 ז"א
ז"א 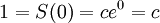 , ומכאן נובע ש-
, ומכאן נובע ש-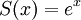 ובפרט
ובפרט 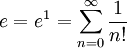 . ו"הוכחנו" את הטענה (לצערנו גזרנו טור אינסופי איבר-איבר, אבל כאמור, אין לנו משפט שאומר שזה נכון).
. ו"הוכחנו" את הטענה (לצערנו גזרנו טור אינסופי איבר-איבר, אבל כאמור, אין לנו משפט שאומר שזה נכון).
טענה: e אינו רציונלי.
הוכחה: נניח בשלילה ש-e רצינלי ונסמן 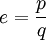 עבור
עבור 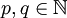 . לכן
. לכן 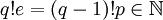 , אבל
, אבל 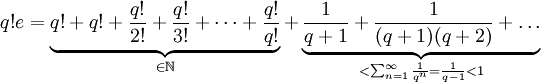 , כלומר
, כלומר 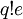 הוא מספר טבעי השווה למספר טבעי ועוד מספר לא שלם, בסתירה.
הוא מספר טבעי השווה למספר טבעי ועוד מספר לא שלם, בסתירה. 
הגדרה: תהי 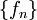 סדרת פונקציות בקטע I כך שלכל
סדרת פונקציות בקטע I כך שלכל 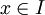 קיים הגבול
קיים הגבול 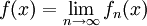 . ניתן שתי הגדרות שקולות לשאיפה של
. ניתן שתי הגדרות שקולות לשאיפה של 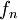 ל-f במידה ושווה ב-I:
ל-f במידה ושווה ב-I:
- לכל
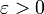 קיים
קיים 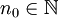 כך שאם
כך שאם 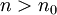 אז
אז 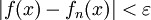 לכל
לכל 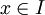 .
. -
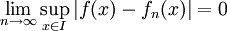 .
.