משתמש:אור שחף/133 - הרצאה/5.4.11
תוכן עניינים
אינטגרל לא אמיתי
הגדרה: תהי f מוגדרת בקטע מהסוג  \. נאמר ש-f אינטגרבילית מקומית ב-
\. נאמר ש-f אינטגרבילית מקומית ב- אם לכל
אם לכל 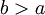 f אינטגרבילית ב-
f אינטגרבילית ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) (locally integrable function).
הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב-
(locally integrable function).
הגדרה: תהי f מוגדרת ואינטגרבילית מקומית ב- . נגדיר
. נגדיר 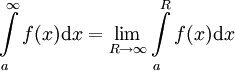 .
אם הגבול קיים אומרים שהאינטגרל מתכנס ו-f אינטגרבילית ב-
.
אם הגבול קיים אומרים שהאינטגרל מתכנס ו-f אינטגרבילית ב- ואם הגגבול לא קים אומרים שהאינטגרל מתבדר \, ו-f לא אינטגרבילית בקטע.
ואם הגגבול לא קים אומרים שהאינטגרל מתבדר \, ו-f לא אינטגרבילית בקטע.
דוגמאות חישוב
-
![\int\limits_1^\infty xe^{-x}\mathrm dx=\lim_{R\to\infty}\int\limits_1^R xe^{-x}\mathrm dx=\lim_{R\to\infty}\left[x'\cdot(-x)e^{-x}\right]_{x=1}^R-\int\limits_1^R -e^{-x}\mathrm dx=\lim_{R\to\infty}-Re^{-R}+e^{-1}-[e^x]_{x=1}^R=\frac2e](/images/math/b/8/3/b839d59813dbeda548756381064f2c53.png) . דרך קיצור:
. דרך קיצור: ![\int\limits_1^\infty xe^{-x}\mathrm dx=[-xe^{-x}]_{x=1}^\infty+\int\limits_1^\infty -e^{-x}\mathrm dx=e^{-1}-[e^{-x}]_{x=1}^\infty=\frac2e](/images/math/1/9/1/1913e67771121c7487f3a4d783d7be64.png) .
. -
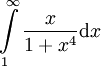 . נציב
. נציב 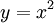 ואז כאשר
ואז כאשר 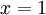 נקבל
נקבל 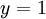 וכאשר
וכאשר 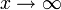 נקבל
נקבל 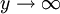 ולכן
ולכן ![\int=\int\limits_1^\infty \frac{\mathrm dy}{1+y^2}\mathrm dy=[\frac12\arctan(y)]_{y=1}^\infty=...](/images/math/6/7/9/679c97ae918c75e9754e78cf450ac70c.png) .
. - עבור
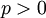 נחשב
נחשב 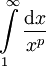 עבור
עבור 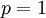 זה
זה ![\int\limits_1^\infty \frac{\mathrm dx}x=[\ln|x|]_{x=1}^\infty=\infty](/images/math/8/d/d/8ddf8650a95bc1fa2455f4b884991c83.png) - מתבדר. עבור
- מתבדר. עבור 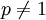 נקבל
נקבל ![[\frac{x^{-p+1}}{-p+1}]_1^\infty=\lim_{x\to\infty}\frac{x-p+1}{-p+1}-\frac1{-p+1}=\begin{cases}\frac1{p-1}&p>1\\\infty&p<1\end{cases}](/images/math/8/0/7/807fea699247b2131b7fd347bf6e6ebd.png) , כלומר האינטגרל מתכנס
, כלומר האינטגרל מתכנס 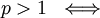 . הערה: עבור
. הערה: עבור 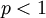 מתקבל
מתקבל 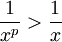 בקטע
בקטע 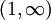 . לכן מבין הפונקציות
. לכן מבין הפונקציות 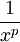 , הפונקציה המינימלית שעבורה האינטגרל על
, הפונקציה המינימלית שעבורה האינטגרל על 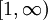 מתבדר היא
מתבדר היא  . אבל יש פונקציה מסדר גודל יותר קטן מ-
. אבל יש פונקציה מסדר גודל יותר קטן מ- שעבורן האינטגרל מתבדר, למשל
שעבורן האינטגרל מתבדר, למשל ![\int\limits_2^\infty\frac x{x\ln(x)}\mathrm dx=\int\limits_2^\infty\frac{1/x}{\ln(x)}\mathrm dx=[\ln(\ln(x))]_{x=2}^\infty=\infty](/images/math/7/3/8/7389d6df908bc69953ae54d7a34cf3d8.png) . "קל לבדוק" שעבור
. "קל לבדוק" שעבור 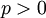 האינטגרל
האינטגרל 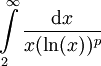 מתכנס אם"ם
מתכנס אם"ם 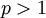 .
. - נניח ש-f מוגדרת ורציפה ב-
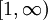 ונניחי ש-
ונניחי ש-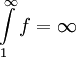 . נבנה פונקציה
. נבנה פונקציה 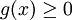 רציפה ב-
רציפה ב-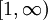 מסדר גודל יותר קטן מ-f: ז"א
מסדר גודל יותר קטן מ-f: ז"א 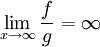 ועדיין
ועדיין 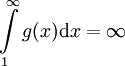 . ובכן נגדיר
. ובכן נגדיר 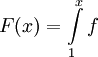 אז כמובן ש-
אז כמובן ש-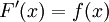 ולפי הנתון
ולפי הנתון 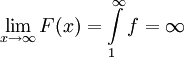 נגדיר
נגדיר 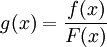 וכן
וכן 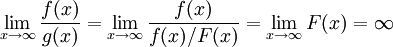 ז"א g מסדר גודל קטן מ-f. כעת עיבוד הנוסחה נכשל (שגיאת תחביר): \int\limits_1^\infty g=\int\limits_1^\infty\frac{f(x)}{F(x)}\mathrm dx=\int\limits_1^\infty \frac{F'(x)}{F(x)}}\mathrm dx=[\ln(F(x))]_{x=1}^\infty=\infty
ז"א g מסדר גודל קטן מ-f. כעת עיבוד הנוסחה נכשל (שגיאת תחביר): \int\limits_1^\infty g=\int\limits_1^\infty\frac{f(x)}{F(x)}\mathrm dx=\int\limits_1^\infty \frac{F'(x)}{F(x)}}\mathrm dx=[\ln(F(x))]_{x=1}^\infty=\infty
.
- נניח ש-
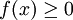 רציפה ב-
רציפה ב-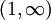 ו-
ו-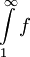 מתכנס. אז קיימת
מתכנס. אז קיימת 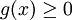 מסדר גודל דגול מ-F כך ש-
מסדר גודל דגול מ-F כך ש-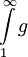 מתכנס.
מתכנס.
בנייה: נגדיר 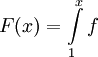 לכן
לכן 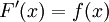 לכן
לכן 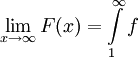 קיים ושווה ל-L. נגדיר
קיים ושווה ל-L. נגדיר 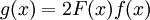 אז g מגדר גודל כמו f וזה לא עוזר, אלא יש להגדיר
אז g מגדר גודל כמו f וזה לא עוזר, אלא יש להגדיר 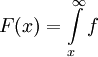 אז שוב
אז שוב 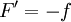 וכיוון שהאינטגרל של f מתכנס,
וכיוון שהאינטגרל של f מתכנס, 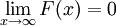 . נגדיר
. נגדיר 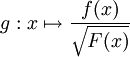 חילקנו את f בפונקציה ששואפת ל-0 באינסוף, ולכן g מסדר גודל יותר גדול מ-f. יתר על כן
חילקנו את f בפונקציה ששואפת ל-0 באינסוף, ולכן g מסדר גודל יותר גדול מ-f. יתר על כן ![\int\limits_1^\infty g=\int\limits_1^\infty\frac{f(x)}\sqrt{F(x)}\mathrm dx=\int\limits_1^\infty\frac{-F(x)}\sqrt{F(x)}\mathrm dx=[-2\sqrt{F(x)}]_{x=1}^\infty=2\sqrt{F(x)}=2\sqrt{\int\limits_1^\infty f}](/images/math/6/7/1/671aae9cf9af70057fb6906c4b84b956.png)
-
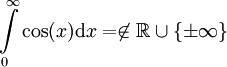 , כלומר האינטגרל מתבדר לחלוטין.
, כלומר האינטגרל מתבדר לחלוטין. - נתבונן באינטגרל
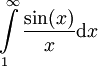 - מתכנס או מתבדר? נוכיך שמתכנס בעזרת משפט לייבניץ על טורים. נבחר N טבעי ןנבטא את האינטגרל החלקי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): \int\limits_1^{N\pi}\sinc(x)\mathrm dx=\sum_{k=1}^N \int\limits_{(k-1)\pi}^{k\pi}\sinc(x)\mathrm dx=\sum_{k=1}^N a_k
- מתכנס או מתבדר? נוכיך שמתכנס בעזרת משפט לייבניץ על טורים. נבחר N טבעי ןנבטא את האינטגרל החלקי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): \int\limits_1^{N\pi}\sinc(x)\mathrm dx=\sum_{k=1}^N \int\limits_{(k-1)\pi}^{k\pi}\sinc(x)\mathrm dx=\sum_{k=1}^N a_k
. טענה: המספרים 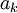 מקיימים:
מקיימים:
-
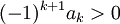
-
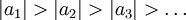 (ולכן הטור שמתפתח הוא טור לייבניץ. הוכחה:
(ולכן הטור שמתפתח הוא טור לייבניץ. הוכחה: - עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): \int\limits_{(k-1)\pi}^{k\pi}\sinc(x)\mathrm dx
. אם k א"ז אז 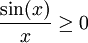 בקטע
בקטע ![[(k-1)\pi,k\pi]](/images/math/e/a/2/ea2a8ada2777316098b00da46203bf30.png) ואם k זוגי אז
ואם k זוגי אז 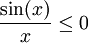 בקטע. לכן הטענה הראשונה מתקיימת.
בקטע. לכן הטענה הראשונה מתקיימת.
- לכל k טבעי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): |a_k|=\left|\int\limits_{(k-1)\pi}^{k\pi}\sinc(x)\mathrm dx\right|=\int\limits_{(k-1)\pi}^{k\pi}\frac{|\sin(x)|}x\mathrm dx
כי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): \sinc(x) בעלת סימן קבוע ב-. נציב
על מנת לקבל
ומכיוון ש-
זה שווה ל-
ואילו
, לכן הטענה השנייה מתקיימת. נותר לנו לבדוק ש-
. ואכן
. לסיכום
וה-
יוצרים טור לייבניץ. ע"פ משפט ליבניץ הטור
מתכנס, נאמר ל-L. טענה - עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): \int_1^\infty \sinc(x)\mathrm dx=L
. הוכחה: יהי 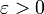 נתון. לפי הנתון קיים
נתון. לפי הנתון קיים 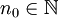 כך שלכל
כך שלכל 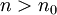 מתקיים
מתקיים 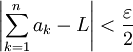 . כמו כן
. כמו כן 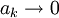 ולכן קיים
ולכן קיים 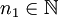 כך שלכל
כך שלכל 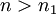 מתקיים
מתקיים 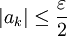 . כעת נגדיר
. כעת נגדיר 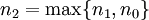 . אם
. אם 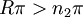 אזי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): |\int_1^{R\pi} \sinc(x)\mathrm dx-L|=|\int\limits_1^{\lfloor R\rfloor\pi} \sinc(x)\mathrm dx+\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx-L|=|\sum_{k=1}^{\lfloor R\rfloor} a_k-L+\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx|\le|\sum_{k=1}^{\lfloor R\rfloor} a_k-L|+|\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx|
\le\frac\varepsilon2+a_{\lfloor R\rfloor}<\varepsilon
אזי עיבוד הנוסחה נכשל (פונקציה \sinc לא מוכרת): |\int_1^{R\pi} \sinc(x)\mathrm dx-L|=|\int\limits_1^{\lfloor R\rfloor\pi} \sinc(x)\mathrm dx+\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx-L|=|\sum_{k=1}^{\lfloor R\rfloor} a_k-L+\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx|\le|\sum_{k=1}^{\lfloor R\rfloor} a_k-L|+|\int\limits_{\lfloor R\rfloor\pi}^{R\pi} \sinc(x)\mathrm dx|
\le\frac\varepsilon2+a_{\lfloor R\rfloor}<\varepsilon
משפט 1
נניח שהפונקציות f ו-g מוגדרות ואינטגרביליות בקטע  ו-c מספר קבוע. אזי הפונקציה
ו-c מספר קבוע. אזי הפונקציה 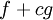 אינטגרבילית ב-
אינטגרבילית ב- ומתקיים
ומתקיים 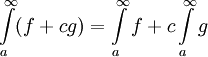 .
.
הוכחה
לפי הגדרה 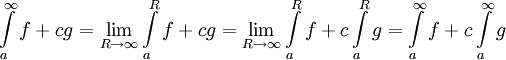

משפט 2
תהי f מוגדר ואינטגרבילית מקומית ב- ויהי
ויהי 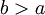 . אזי האינטגרל
. אזי האינטגרל 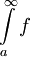 מתכנס אם"ם
מתכנס אם"ם  מתכנס, ואם כן
מתכנס, ואם כן 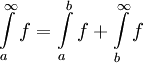 . ההוכחה פשוטה מדי.
. ההוכחה פשוטה מדי.
משפט 3
- תהי f מוגדרת ועולה בקטע
 אזי
אזי 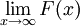 קיים אם"ם
קיים אם"ם 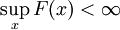 , ואם כן
, ואם כן 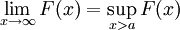 .
. - תהי f מוגדרת ואינטגרבילית מקומית ב-
 . עוד נניח ש-
. עוד נניח ש-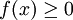 בקטע זה, אזי
בקטע זה, אזי 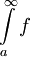 מתכנס אם"ם האינטגרלים החלקיים
מתכנס אם"ם האינטגרלים החלקיים 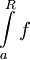 חסומים מלעיל.
חסומים מלעיל.
הוכחות
- נניח
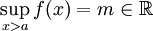 . טענה:
. טענה: 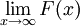 קיים ושווה ל-m. הוכחה: לפי אפיון החסם העליון, אם
קיים ושווה ל-m. הוכחה: לפי אפיון החסם העליון, אם 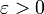 נתון אזי קיים
נתון אזי קיים 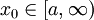 כך ש-
כך ש-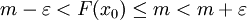 לכן עבור כל
לכן עבור כל 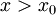 מתקיים (מכיוון ש-f עולה)
מתקיים (מכיוון ש-f עולה) 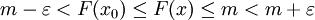 . בפרט, לכל
. בפרט, לכל 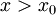 מתקיים
מתקיים 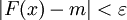 ולכן
ולכן 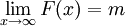 ואם
ואם 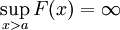 (לא חסום) אז לכל
(לא חסום) אז לכל 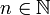 קיים
קיים 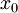 כך ש-
כך ש-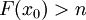 . כעת, אם
. כעת, אם 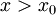 אז
אז 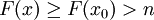 . נובע ש-
. נובע ש-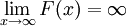 ואין גבול במובן הצר.
ואין גבול במובן הצר. - לכל
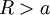 נגדיר
נגדיר 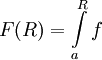 . כיוון ש-
. כיוון ש-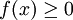 לכל
לכל 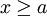 ,
, 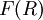 עולה עם R. האינטגרל הלא אמיתי
עולה עם R. האינטגרל הלא אמיתי 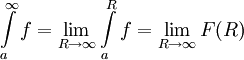 וראינו בחלק 1 שהגבול של
וראינו בחלק 1 שהגבול של 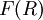 קיים אם"ם
קיים אם"ם 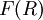 חסומה מלעיל, ז"א אם"ם
חסומה מלעיל, ז"א אם"ם 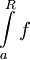 חסום מלעיל כאשר
חסום מלעיל כאשר 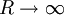 .
. 
מסקנה
מתוך ההוכחה ראינו שאם האינטגרל מתבדר אז הוא מתכנס במובן הרחב ל-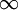 .
.