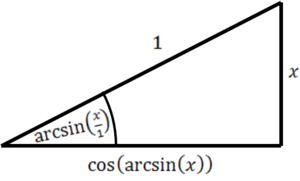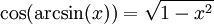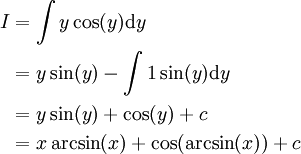הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - הרצאה/6.3.11"
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
מ (←דוגמאות חישוב) |
מ |
||
| שורה 1: | שורה 1: | ||
=האינטגרל הלא מסויים= | =האינטגרל הלא מסויים= | ||
| − | '''הגדרה:''' אינטגרל מסויים הוא אינטגרל עם גבולות <math>\int\limits_a^b f</math> שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות - <math>\int f</math>, שפתרונו פשוט <math>F(x)+c</math> עבור F פונקציה קדומה ל-f. | + | '''הגדרה:''' אינטגרל מסויים הוא אינטגרל עם גבולות <math>\int\limits_a^b f</math> שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות - <math>\int f</math>, שפתרונו פשוט <math>F(x)+c</math> עבור F פונקציה קדומה ל-f וקבוע c. |
==אינטגרלים פשוטים== | ==אינטגרלים פשוטים== | ||
| שורה 6: | שורה 6: | ||
<math>\begin{array}{l r|l} | <math>\begin{array}{l r|l} | ||
| − | \underline{f(x)} && \underline{\int f(x)\mathrm dx\ {\color{Gray}-\text{ constant}}}\\ | + | \underline{f(x)} && \underline{\int f(x)\mathrm dx\ {\color{Gray}-\text{constant}}}\\ |
c && cx\\ | c && cx\\ | ||
| שורה 26: | שורה 26: | ||
===בדיקות=== | ===בדיקות=== | ||
# נבדוק <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac1x</math> (עבור <math>x\ne0</math>): לפי ההגדרה <math>\ln|x|=\begin{cases}\ln(x)&x>0\\\ln(-x)&x<0\end{cases}</math>. לכן עבור <math>x>0</math> מתקיים <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac\mathrm d{\mathrm dx}\ln(x)=\frac1x</math> ועבור <math>x<0</math>, <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac\mathrm d{\mathrm dx}\ln(-x)=-\frac1{-x}=\frac1x</math>. {{משל}} | # נבדוק <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac1x</math> (עבור <math>x\ne0</math>): לפי ההגדרה <math>\ln|x|=\begin{cases}\ln(x)&x>0\\\ln(-x)&x<0\end{cases}</math>. לכן עבור <math>x>0</math> מתקיים <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac\mathrm d{\mathrm dx}\ln(x)=\frac1x</math> ועבור <math>x<0</math>, <math>\frac\mathrm d{\mathrm dx}\ln|x|=\frac\mathrm d{\mathrm dx}\ln(-x)=-\frac1{-x}=\frac1x</math>. {{משל}} | ||
| − | # <math>\frac\mathrm d{\mathrm dx}\frac1a\arctan\left(\frac xa\right)=\frac1a\frac1{1+\left(\frac xa\right)^2}\frac1a=\frac1{a^2+x^2}</math> {{משל}} | + | # <math>\frac\mathrm d{\mathrm dx}\frac1a\arctan\left(\frac xa\right)=\frac1a\frac1{1+\left(\frac xa\right)^2}\frac1a=\frac1{a^2+x^2}</math>. {{משל}} |
| − | # <math>\frac\mathrm d{\mathrm dx}\arcsin\left(\frac xa\right)=\frac1\sqrt{1-\left(\frac xa\right)^2}\frac1a=\frac1\sqrt{a^2-x^2}</math> {{משל}} | + | # <math>\frac\mathrm d{\mathrm dx}\arcsin\left(\frac xa\right)=\frac1\sqrt{1-\left(\frac xa\right)^2}\frac1a=\frac1\sqrt{a^2-x^2}</math>. {{משל}} |
===דוגמאות חישוב=== | ===דוגמאות חישוב=== | ||
| שורה 37: | שורה 37: | ||
# <math>\int\sin\left(x^2\right)\mathrm dx\ne\frac{-\cos(x^2)}{2}+c</math><div dir="rtl" align="right">(למעשה, האינטגרל הזה לא אלמנטרי)</div> | # <math>\int\sin\left(x^2\right)\mathrm dx\ne\frac{-\cos(x^2)}{2}+c</math><div dir="rtl" align="right">(למעשה, האינטגרל הזה לא אלמנטרי)</div> | ||
# <math>\int3^xe^x\mathrm dx=\int(3e)^x\mathrm dx=\frac{(3e)^x}{\ln(3e)}+c=\frac{(3e)^x}{1+\ln(3)}+c</math> | # <math>\int3^xe^x\mathrm dx=\int(3e)^x\mathrm dx=\frac{(3e)^x}{\ln(3e)}+c=\frac{(3e)^x}{1+\ln(3)}+c</math> | ||
| − | # <math>\int\tan(x)\mathrm dx=\int(\sec^2(x)-1)\mathrm dx=\tan(x)-x+c</math> | + | # <math>\int\tan^2(x)\mathrm dx=\int(\sec^2(x)-1)\mathrm dx=\tan(x)-x+c</math> |
| − | # <math>\int\frac{1+\cos(x)}{1+\cos^2(2x)}\mathrm dx= | + | # <math>\int\frac{1+\cos(x)}{1+\cos^2(2x)}\mathrm dx=?</math><div dir="rtl" align="right">(הפונקציה אלמנטרית אבל האינטגרל לא ידוע לנו. המסר הוא שהאינטגרציה קשה)</div> |
# <span id="partial_fraction_example"><!-- אל תמחקו span זה. הוא משמש להפנייה לסעיף זה של הדוגמה --></span><math>\begin{align}\int\frac1{(x-3)(x-4)}\mathrm dx&=\int\frac{(x-3)-(x-4)}{(x-3)(x-4)}\mathrm dx\\&=\int\frac{\mathrm dx}{x-4}-\int\frac{\mathrm dx}{x-3}\\&=\ln|x-4|-\ln|x-3|+c\end{align}</math> | # <span id="partial_fraction_example"><!-- אל תמחקו span זה. הוא משמש להפנייה לסעיף זה של הדוגמה --></span><math>\begin{align}\int\frac1{(x-3)(x-4)}\mathrm dx&=\int\frac{(x-3)-(x-4)}{(x-3)(x-4)}\mathrm dx\\&=\int\frac{\mathrm dx}{x-4}-\int\frac{\mathrm dx}{x-3}\\&=\ln|x-4|-\ln|x-3|+c\end{align}</math> | ||
}} | }} | ||
| שורה 45: | שורה 45: | ||
==אינטגרציה בחלקים== | ==אינטגרציה בחלקים== | ||
| − | כזכור, אם f ו-g פונקציות גזירות אז <math>\frac\mathrm d{\mathrm dx}f(x)g(x)=f(x)g'(x)+f'(x)g(x)</math>. אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה: | + | כזכור, אם f ו-g פונקציות גזירות אז <math>\frac\mathrm d{\mathrm dx}f(x)g(x)=f(x)g'(x)+f'(x)g(x)</math>. אם {{ltr|f'}} ו-{{ltr|g'}} רציפות נוכל להפוך את זה לנוסחת אינטגרציה: |
<math>\int f(x)g'(x)\mathrm dx=f(x)g(x)-\int f'(x)g(x)\mathrm dx</math>. | <math>\int f(x)g'(x)\mathrm dx=f(x)g(x)-\int f'(x)g(x)\mathrm dx</math>. | ||
| שורה 54: | שורה 54: | ||
# <math>\int x^3\ln(x)\mathrm dx=\frac{x^4}4\ln(x)-\int\frac1x\frac{x^4}4\mathrm dx=\frac{x^4}4\ln(x)-\frac{x^4}{16}+c</math>. | # <math>\int x^3\ln(x)\mathrm dx=\frac{x^4}4\ln(x)-\int\frac1x\frac{x^4}4\mathrm dx=\frac{x^4}4\ln(x)-\frac{x^4}{16}+c</math>. | ||
# <math>\int\ln(x)\mathrm dx=\int1\ln(x)\mathrm dx=x\ln(x)-\int\frac1xx\mathrm dx=x\ln(x)-x+c</math>. | # <math>\int\ln(x)\mathrm dx=\int1\ln(x)\mathrm dx=x\ln(x)-\int\frac1xx\mathrm dx=x\ln(x)-x+c</math>. | ||
| − | # <math>\begin{align}\int e^x\cos(x)\mathrm dx&=e^x\sin(x)-\int e^x\sin(x)\mathrm dx\\&=e^x\sin(x)+e^x\cos(x) | + | # <math>\begin{align}\int e^x\cos(x)\mathrm dx&=e^x\sin(x)-\int e^x\sin(x)\mathrm dx\\&=e^x\sin(x)+e^x\cos(x)-\int e^x\cos(x)\mathrm dx\end{align}</math> ולכן <math>\int e^x\cos(x)\mathrm dx=\frac{e^x}2\Big(\sin(x)+\cos(x)\Big)+c</math>. |
==שיטת ההצבה/שינוי משתנים== | ==שיטת ההצבה/שינוי משתנים== | ||
| שורה 67: | שורה 67: | ||
# <math>\int\frac{\ln(x)}x\mathrm dx</math>: נציב <math>y=\ln(x)</math> ואז <math>\mathrm dy=\frac1x\mathrm dx</math> ונובע ש-<math>I=\int y\mathrm dy=\frac{y^2}2+c=\frac12(\ln(x))^2+c</math>. | # <math>\int\frac{\ln(x)}x\mathrm dx</math>: נציב <math>y=\ln(x)</math> ואז <math>\mathrm dy=\frac1x\mathrm dx</math> ונובע ש-<math>I=\int y\mathrm dy=\frac{y^2}2+c=\frac12(\ln(x))^2+c</math>. | ||
# <math>\int\frac x\sqrt{x^2+1}\mathrm dx</math>: נציב <math>y=x^2+1\implies\mathrm dy=2x\mathrm dx</math> ולכן <math>I=\int\frac{\tfrac12\mathrm dy}\sqrt y=\frac12\int y^{-\frac12}\mathrm dy=y^{\frac12}+c=\sqrt{x^2+1}+c</math>. | # <math>\int\frac x\sqrt{x^2+1}\mathrm dx</math>: נציב <math>y=x^2+1\implies\mathrm dy=2x\mathrm dx</math> ולכן <math>I=\int\frac{\tfrac12\mathrm dy}\sqrt y=\frac12\int y^{-\frac12}\mathrm dy=y^{\frac12}+c=\sqrt{x^2+1}+c</math>. | ||
| − | # <math>\int\tan(x)\mathrm dx</math>: עבור <math>y=\cos(x)</math> נקבל <math>I=\int\frac{\sin(x)}{\cos(x)}\mathrm dx=\int\frac{-\mathrm dy}y=-\ln|y|+c=-\ln|\cos(x)|+c</math>. | + | # <math>\int\tan(x)\mathrm dx</math>: עבור <math>y=\cos(x)</math> נקבל <math>I=\int\frac{\sin(x)}{\cos(x)}\mathrm dx=\int\frac{-\mathrm dy}y=-\ln|y|+c=-\ln|\cos(x)|+c=\ln|\sec(x)|+c</math>. |
# <math>\int\cot(x)\mathrm dx=\int\frac{\cos(x)}{\sin(x)}\mathrm dx=\ln|\sin(x)|+c</math>. | # <math>\int\cot(x)\mathrm dx=\int\frac{\cos(x)}{\sin(x)}\mathrm dx=\ln|\sin(x)|+c</math>. | ||
#<math>\int\frac{f'(x)}{f(x)}\mathrm dx</math>: נציב <math>y=f(x)</math> ונקבל <math>I=\int\frac{\mathrm dy}y=\ln|y|+c=\ln|f(x)|+c</math>.<br />לכן ניתן להוכיח שוב את סעיף 4: <math>\int\tan(x)\mathrm dx=-\int\frac{\cos'(x)}{\cos(x)}\mathrm dx=-\ln|\cos(x)|+c</math>. | #<math>\int\frac{f'(x)}{f(x)}\mathrm dx</math>: נציב <math>y=f(x)</math> ונקבל <math>I=\int\frac{\mathrm dy}y=\ln|y|+c=\ln|f(x)|+c</math>.<br />לכן ניתן להוכיח שוב את סעיף 4: <math>\int\tan(x)\mathrm dx=-\int\frac{\cos'(x)}{\cos(x)}\mathrm dx=-\ln|\cos(x)|+c</math>. | ||
# <math>\int\frac{f'(x)}{f^2(x)}\mathrm dx</math>: נציב <math>y=f(x)</math> ונקבל <math>I=\int\frac{\mathrm dy}{y^2}=-\frac1y+c=-\frac1{f(x)}+c</math>. | # <math>\int\frac{f'(x)}{f^2(x)}\mathrm dx</math>: נציב <math>y=f(x)</math> ונקבל <math>I=\int\frac{\mathrm dy}{y^2}=-\frac1y+c=-\frac1{f(x)}+c</math>. | ||
# <math>\int\frac{x^5\mathrm dx}\sqrt{1-x^3}</math>: נציב <math>y=1-x^3</math> ואז <math>\frac{(1-y)\mathrm dy}{-3}=x^5\mathrm dx</math>. מכאן ש-<math>I=\int\frac{\frac{1-y}{-3}\mathrm dy}\sqrt y=\int\left(\frac13\sqrt y-\frac1{\sqrt y}\right)\mathrm dy=\frac29\sqrt{1-x^3}^3-\frac23\sqrt{1-x^3}+c</math>. | # <math>\int\frac{x^5\mathrm dx}\sqrt{1-x^3}</math>: נציב <math>y=1-x^3</math> ואז <math>\frac{(1-y)\mathrm dy}{-3}=x^5\mathrm dx</math>. מכאן ש-<math>I=\int\frac{\frac{1-y}{-3}\mathrm dy}\sqrt y=\int\left(\frac13\sqrt y-\frac1{\sqrt y}\right)\mathrm dy=\frac29\sqrt{1-x^3}^3-\frac23\sqrt{1-x^3}+c</math>. | ||
| − | # <math>\int\arcsin(x)\mathrm dx</math>: נציב <math>y=\arcsin(x)</math> ומכאן ש-<math>\mathrm dx=\cos(y)\mathrm dy</math>. לבסוף, {{left|<math>\begin{align}I&=\int y\cos(y)\mathrm dy\\&=y\sin(y)-\int1\sin(y)\mathrm dy\\&=y\sin(y)+\cos(y)\\&=x\arcsin(x)+\cos(\arcsin(x))+c\end{align}</math>}} | + | # <math>\int\arcsin(x)\mathrm dx</math>: נציב <math>y=\arcsin(x)</math> ומכאן ש-<math>\mathrm dx=\cos(y)\mathrm dy</math>. לבסוף, {{left|[[קובץ:חישושב קוסינוס של ארקסינוס.png|שמאל|300px|ממוזער|ממשפט פיתגורס ומהסרטוט נובע כי <math>\cos(\arcsin(x))=\sqrt{1-x^2}</math>]]<math>\begin{align}I&=\int y\cos(y)\mathrm dy\\&=y\sin(y)-\int1\sin(y)\mathrm dy\\&=y\sin(y)+\cos(y)+c\\&=x\arcsin(x)+\cos(\arcsin(x))+c\end{align}</math>}} ולכן <math>I=x\arcsin(x)+\sqrt{1-x^2}+c</math>.<br />דרך אחרת: <math>I=\int1\arcsin(x)\mathrm dx=x\arcsin(x)-\int\frac x\sqrt{1-x^2}\mathrm dx</math>. נגדיר <math>y=1-x^2</math> ושוב נקבל {{left|<math>\begin{align}I&=x\arcsin(x)-\int\frac x\sqrt{1-x^2}\mathrm dx\\&=x\arcsin(x)+\int\frac{\mathrm dy}{2\sqrt y}\\&=x\arcsin(x)-\sqrt y+c\\&=x\arcsin(x)+\sqrt{1-x^2}+c\end{align}</math>}} |
# <math>\int e^\sqrt x\mathrm dx</math>: נציב <math>y=\sqrt x\implies\mathrm dy=\frac{\mathrm dx}{2\sqrt x}</math> ולכן <math>I=\int 2ye^y\mathrm dy=2ye^y-\int2e^y\mathrm dy=2\sqrt xe^\sqrt x-2e^\sqrt x+c</math>. | # <math>\int e^\sqrt x\mathrm dx</math>: נציב <math>y=\sqrt x\implies\mathrm dy=\frac{\mathrm dx}{2\sqrt x}</math> ולכן <math>I=\int 2ye^y\mathrm dy=2ye^y-\int2e^y\mathrm dy=2\sqrt xe^\sqrt x-2e^\sqrt x+c</math>. | ||
# <math>\int\sin(x)\cos(x)\mathrm dx</math>: נבחר <math>y=\sin(x)</math> כדי לקבל <math>I=\int y\mathrm dy=\frac12y^2+c=\frac12\sin^2(x)+c</math>.<br />שיטה אחרת: <math>y=\cos(x)</math> ואז <math>I=\int-y\mathrm dy=-\frac12\cos^2(x)+c</math>.<br />שיטה אחרונה: <math>I=\int\frac12\sin(2x)\mathrm dx=-\frac14\cos(2x)+c</math>.<br />קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל: <math>\frac12\sin^2(x)-\left(-\frac12\cos^2(x)\right)=\frac12\left(\cos^2(x)+\sin^2(x)\right)=\frac12</math>. | # <math>\int\sin(x)\cos(x)\mathrm dx</math>: נבחר <math>y=\sin(x)</math> כדי לקבל <math>I=\int y\mathrm dy=\frac12y^2+c=\frac12\sin^2(x)+c</math>.<br />שיטה אחרת: <math>y=\cos(x)</math> ואז <math>I=\int-y\mathrm dy=-\frac12\cos^2(x)+c</math>.<br />שיטה אחרונה: <math>I=\int\frac12\sin(2x)\mathrm dx=-\frac14\cos(2x)+c</math>.<br />קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל: <math>\frac12\sin^2(x)-\left(-\frac12\cos^2(x)\right)=\frac12\left(\cos^2(x)+\sin^2(x)\right)=\frac12</math>. | ||
גרסה מ־13:05, 11 ביולי 2011
תוכן עניינים
האינטגרל הלא מסויים
הגדרה: אינטגרל מסויים הוא אינטגרל עם גבולות  שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות -
שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות - 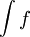 , שפתרונו פשוט
, שפתרונו פשוט 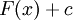 עבור F פונקציה קדומה ל-f וקבוע c.
עבור F פונקציה קדומה ל-f וקבוע c.
אינטגרלים פשוטים

בדיקות
- נבדוק
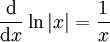 (עבור
(עבור 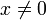 ): לפי ההגדרה
): לפי ההגדרה 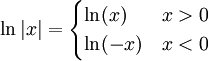 . לכן עבור
. לכן עבור 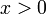 מתקיים
מתקיים 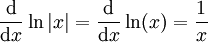 ועבור
ועבור 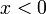 ,
, 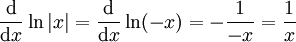 .
. 
-
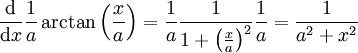 .
. 
-
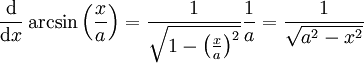 .
. 
דוגמאות חישוב
-
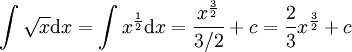
-
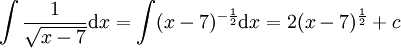
-
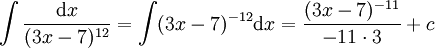 (מהפיכת כלל השרשרת)
(מהפיכת כלל השרשרת) -
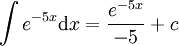
-
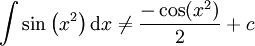 (למעשה, האינטגרל הזה לא אלמנטרי)
(למעשה, האינטגרל הזה לא אלמנטרי) -
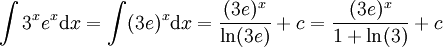
-
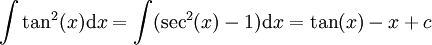
-
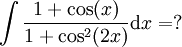 (הפונקציה אלמנטרית אבל האינטגרל לא ידוע לנו. המסר הוא שהאינטגרציה קשה)
(הפונקציה אלמנטרית אבל האינטגרל לא ידוע לנו. המסר הוא שהאינטגרציה קשה) -
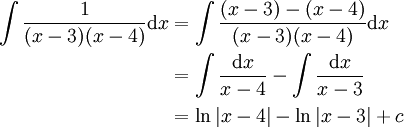
כלל פשוט: האינטגרל לינארי, כלומר 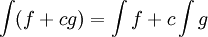 .
.
אינטגרציה בחלקים
כזכור, אם f ו-g פונקציות גזירות אז 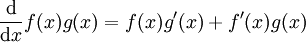 . אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
. אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
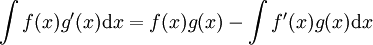 .
.
דוגמאות חישוב
-
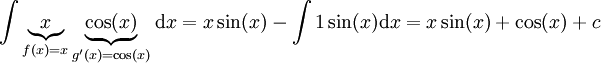 . אם ננסה לפתור אינטגרל זה בדרך הפוכה נקבל
. אם ננסה לפתור אינטגרל זה בדרך הפוכה נקבל 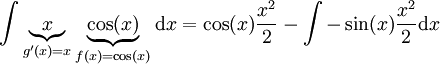 , ואינטגרל זה יותר קשה מהאינטגרל המקורי.
, ואינטגרל זה יותר קשה מהאינטגרל המקורי. -
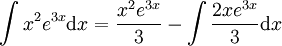 . נעשה שוב אינטגרציה בחלקים:
. נעשה שוב אינטגרציה בחלקים: 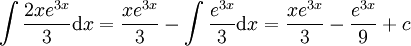 ובסה"כ
ובסה"כ 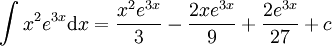 .
. -
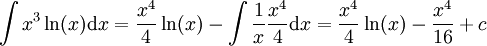 .
. -
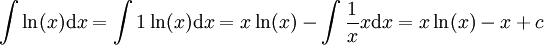 .
. -
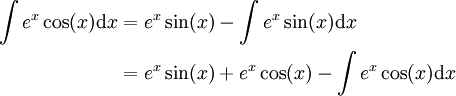 ולכן
ולכן 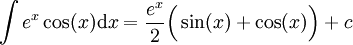 .
.
שיטת ההצבה/שינוי משתנים
נתחיל עם כלל השרשרת: 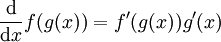 . לכן אם F קדומה ל-f אז
. לכן אם F קדומה ל-f אז 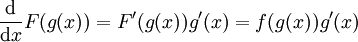 ולפיכך
ולפיכך 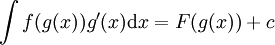 .
.
דרך פורמלית וכללית לפתרון: נתון 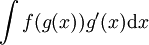 . ע"י הגדרה
. ע"י הגדרה 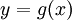 נקבל
נקבל 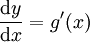 . נעביר אגף:
. נעביר אגף: 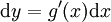 , נחזור לאינטגרל ונקבל
, נחזור לאינטגרל ונקבל 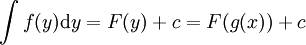 .
.
דוגמאות חישוב
בכל אחת מהדוגמאות הבאות נסמן את האינטגרל שיש לחשב כ-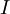 :
:
-
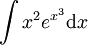 : נציב
: נציב 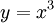 ולכן
ולכן 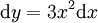 ולפיכך
ולפיכך 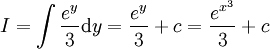 .
. -
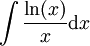 : נציב
: נציב 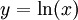 ואז
ואז 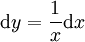 ונובע ש-
ונובע ש-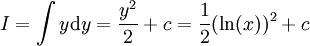 .
. -
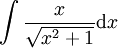 : נציב
: נציב 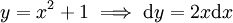 ולכן
ולכן 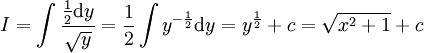 .
. -
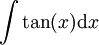 : עבור
: עבור 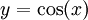 נקבל
נקבל 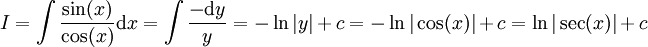 .
. -
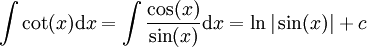 .
. 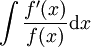 : נציב
: נציב 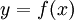 ונקבל
ונקבל 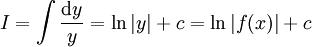 .
.
לכן ניתן להוכיח שוב את סעיף 4: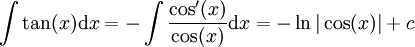 .
.-
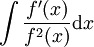 : נציב
: נציב 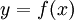 ונקבל
ונקבל 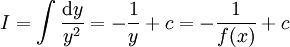 .
. -
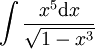 : נציב
: נציב 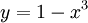 ואז
ואז 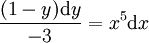 . מכאן ש-
. מכאן ש-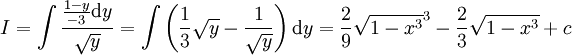 .
. -
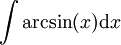 : נציב
: נציב 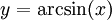 ומכאן ש-
ומכאן ש-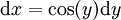 . לבסוף, ולכן
. לבסוף, ולכן 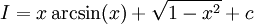 .
.
דרך אחרת: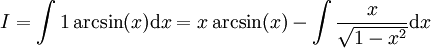 . נגדיר
. נגדיר 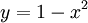 ושוב נקבל
ושוב נקבל 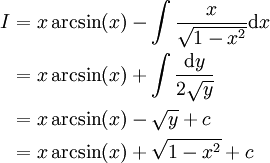
-
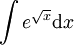 : נציב
: נציב 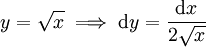 ולכן
ולכן 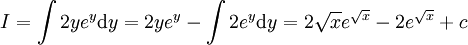 .
. -
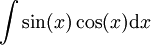 : נבחר
: נבחר 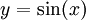 כדי לקבל
כדי לקבל 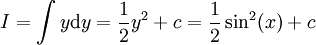 .
.
שיטה אחרת: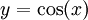 ואז
ואז 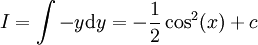 .
.
שיטה אחרונה: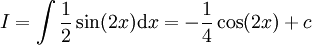 .
.
קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל: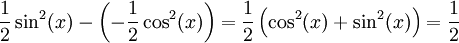 .
.