משתמש:אור שחף/133 - הרצאה/6.3.11
הגדרה: אינטגרל מסויים הוא אינטגרל עם גבולות  שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות -
שלמדנו עד עכשיו - גבול של סכומי רימן וסכומי דרבו. אם f רציפה ניתן, לפעמים, לחשב את האינטגרל לפי נוסחת ניוטון-לייבניץ. השלב העיקרי בחישוב זה הוא מציאת הפונקציה הקדומה, ולכן הגדירו אינטגרל לא מסויים - ללא גבולות - 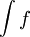 , שפתרונו פשוט
, שפתרונו פשוט 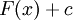 עבור F פונקציה קדומה ל-f.
עבור F פונקציה קדומה ל-f.
טבלה של אינטגרלים פשוטים:
עיבוד הנוסחה נכשל (שגיאת לקסינג): \begin{array}{l|l} f(x) & \int f(x)\mathrm dx\text{\color{gray}+constant}\\ \hline c & cx\\ x^\alpha\quad(\alpha\ne-1) & \frac{x^{\alpha+1}}{\alpha+1}\\ x^{-1} & \ln|x|\\ \sin(x) & -\cos(x)\\ \cos(x) & \sin(x)\\ \sec^2(x) & \tan(x)\\ e^x & e^x\\ a^x\quad(1\ne a>0) & \frac{a^x}{\ln(a)}\\ \frac1{1+x^2} & \arctan\left(\frac xa\right)\\ \frac1\sqrt{1-x^2} & \arcsin(x)\\ \frac1\sqrt{a^2-x^2} & \arcsin\left(\frac xa\right) \end{array}
תוכן עניינים
בדיקות
- נבדוק
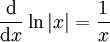 (עבור
(עבור 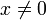 ): לפי ההגדרה
): לפי ההגדרה 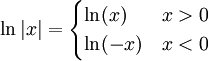 . לכן עבור
. לכן עבור 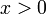 מתקיים
מתקיים 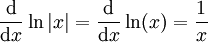 ועבור
ועבור 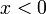 ,
, 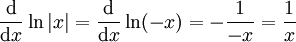 .
. 
- עיבוד הנוסחה נכשל (שגיאת תחביר): \begin{align}\frac\mathrm d{\mathrm dx}\frac1a\arctan\left(\frac xa\right)=\frac1a\frac1{1+\left(\frac xa\right)^2\frac1a\end{align}
דוגמאות חישוב
-
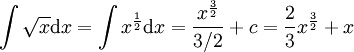
-
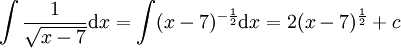
-
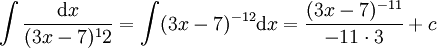 (מהפיכת כלל השרשרת)
(מהפיכת כלל השרשרת) -
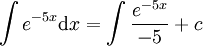
-
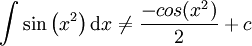 (למעשה, האינטגרל לא אלמנטרי)
(למעשה, האינטגרל לא אלמנטרי) -
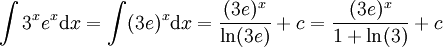
-
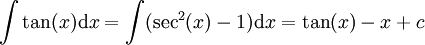
-
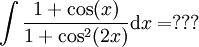 (למרות שהפונקציה אלמנטרית אנו לא יודעים. המסר הוא שהאינטגרציה קשה)
(למרות שהפונקציה אלמנטרית אנו לא יודעים. המסר הוא שהאינטגרציה קשה) - עיבוד הנוסחה נכשל (שגיאת תחביר): \frac{\mathrm dx}{(x-3)(x-4)}=\int\frac{(x-3)-(x-4)}{(x-3)(x-4)}\mathrm dx=\int\frac1\{\mathrm dx}{x-3}+\frac{\mathrm dx}{x-4}=\ln|x-3|+\ln|x-4|+c
כלל פשוט: האינטגרל לינארי, כלומר 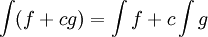 .
.
אינטגרציה בחלקים
כזכור, אם f ו-g פונקציות גזירות אז 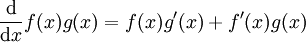 . אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
. אם f' ו-g' רציפות נוכל להפוך את זה לנוסחת אינטגרציה:
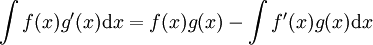 .
.
דוגמאות חישוב
-
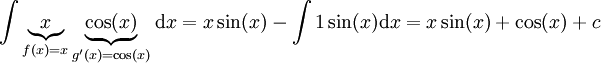 . אם ננסה לפתור אינטגרל זה בדרך הפוכה
. אם ננסה לפתור אינטגרל זה בדרך הפוכה 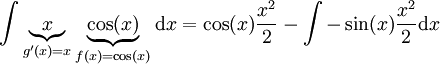 , ואינטגרל זה יותר קשה מהאינטגרל המקורי.
, ואינטגרל זה יותר קשה מהאינטגרל המקורי. -
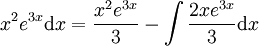 . נעשה שוב אינטגרציה בחלקים: עיבוד הנוסחה נכשל (שגיאת תחביר): \int\frac{2xe^{3x}}3\mathrm dx=\frac{xe^{3x}3-\int\frac{e^{3x}}3\mathrm dx=\frac{xe^{3x}3-\frac{e^{3x}}9+c
. נעשה שוב אינטגרציה בחלקים: עיבוד הנוסחה נכשל (שגיאת תחביר): \int\frac{2xe^{3x}}3\mathrm dx=\frac{xe^{3x}3-\int\frac{e^{3x}}3\mathrm dx=\frac{xe^{3x}3-\frac{e^{3x}}9+c
ובסה"כ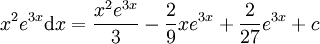
-
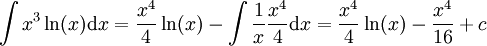
-
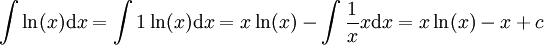
-
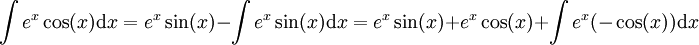 ולכן
ולכן 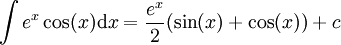
שיטת ההצבה או שינוי משתנים
נתחיל עם כלל השרשרת 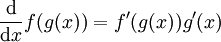 , לכן אם F קדומה ל-f אז
, לכן אם F קדומה ל-f אז 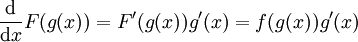 ולפיכך
ולפיכך 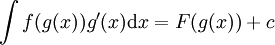
יש דרך פורמלית לפתור 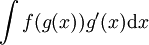 ע"י "הצבה"
ע"י "הצבה" 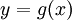 . אם כן
. אם כן 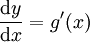 . נעביר אגף
. נעביר אגף 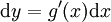 . נחזור לאינטגרל ונקבל
. נחזור לאינטגרל ונקבל 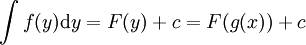
דוגמאות חישוב
-
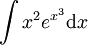 . נציב
. נציב 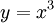 ולכן
ולכן 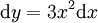 ולכן האינטגרל שווה ל-
ולכן האינטגרל שווה ל-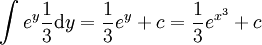
-
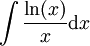 . נציב
. נציב 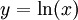 ואז
ואז 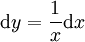 והאינטגרל הוא
והאינטגרל הוא 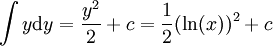
-
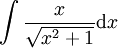 . נציב
. נציב 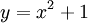 והאינטגרל שווה ל-
והאינטגרל שווה ל-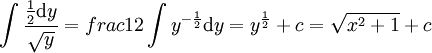
-
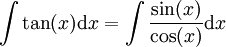 ועבור
ועבור 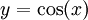 נקבל
נקבל 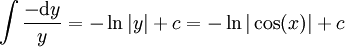
-
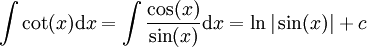
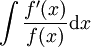 . נציב
. נציב 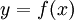 ונקבל
ונקבל 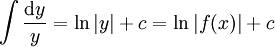 . לכן ניתן להוכיח שוב את סעיף
. לכן ניתן להוכיח שוב את סעיף 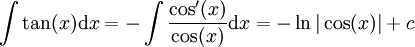 .
.-
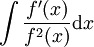 . נציב
. נציב 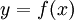 ונקבל
ונקבל 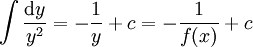
-
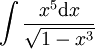 . נציב
. נציב 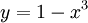 ואז
ואז 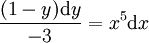 . האינטגרל שווה ל-
. האינטגרל שווה ל-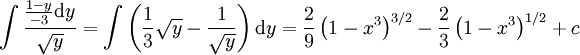
-
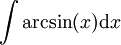 נציב
נציב 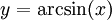 ומכאן ש-
ומכאן ש-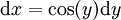 מכאן שהאינטגרל הוא עיבוד הנוסחה נכשל (פונקציה \amthrm לא מוכרת): \int y\cos(y)\mathrm dy=y\sin(y)-\int1\sin(y)\amthrm dy=y\sin(y)+\cos(y)=x\arcsin(x)+\cos(\arcsin(x))+c
מכאן שהאינטגרל הוא עיבוד הנוסחה נכשל (פונקציה \amthrm לא מוכרת): \int y\cos(y)\mathrm dy=y\sin(y)-\int1\sin(y)\amthrm dy=y\sin(y)+\cos(y)=x\arcsin(x)+\cos(\arcsin(x))+c
. גרף (1). דרך אחרת: 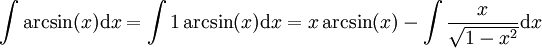 . נגדיר
. נגדיר 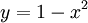 ונקבל
ונקבל 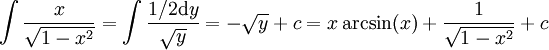
-
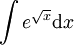 . נציב
. נציב 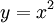 לקבל
לקבל 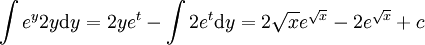 .
. -
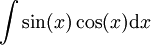 . נבחר
. נבחר 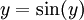 לקבל
לקבל 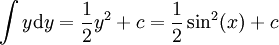 . שיטה אחרת:
. שיטה אחרת: 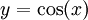 ו-עיבוד הנוסחה נכשל (פונקציה \iny לא מוכרת): \iny-y\mathrm dy=-\frac12\cos^2(x)+c
ו-עיבוד הנוסחה נכשל (פונקציה \iny לא מוכרת): \iny-y\mathrm dy=-\frac12\cos^2(x)+c
. שיטה אחרונה: 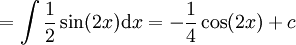 . קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל:
. קיבלנו 3 תשובות שונות באותו תרגיל, אך אין סתירה כי ההפרש בין כל שתי תשובות הוא גודל קבוע. למשל: