משתמש:אור שחף/133 - תרגול/1.5.11
תוכן עניינים
אינטגרלים לא אמיתיים
מקרה ראשון
לפחות אחד מגבולות האינטגרל הוא אינסוף.
דוגמה 1
הראה כי 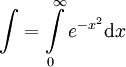 מתכנס ומצא חסם עליון.
מתכנס ומצא חסם עליון.
פתרון
ברור כי 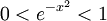 עבור הקטע
עבור הקטע ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , שם נפעיל את האינטגרל:
, שם נפעיל את האינטגרל: 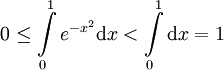 . עבור הקטע
. עבור הקטע 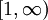 , שם ברור כי מתקיים
, שם ברור כי מתקיים 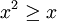 , לכן
, לכן 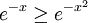 ואז עיבוד הנוסחה נכשל (פונקציה \limtis לא מוכרת): \int\limits_1^\infty e^{-x^2}\mathrm dx\le\int\limtis_1^\infty e^{-x}\mathrm dx=\left[-e^{-x}\right]_{x=1}^\infty=\frac1e
. לכן בסה"כ
ואז עיבוד הנוסחה נכשל (פונקציה \limtis לא מוכרת): \int\limits_1^\infty e^{-x^2}\mathrm dx\le\int\limtis_1^\infty e^{-x}\mathrm dx=\left[-e^{-x}\right]_{x=1}^\infty=\frac1e
. לכן בסה"כ 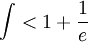 .
.
מבחן דיריכלה
f ו-g רציפות. אם
- f יורדת לאפס.
- הנגגזרת של f רציפה.
-
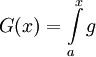 חסומה.
חסומה.
אזי 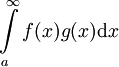 מתכנס.
מתכנס.
דוגמה 2
הוכיחו כי לכל 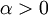 האינטגרל עיבוד הנוסחה נכשל (פונקציה \matghm לא מוכרת): \int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\matghm dx
האינטגרל עיבוד הנוסחה נכשל (פונקציה \matghm לא מוכרת): \int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\matghm dx
מתכנס.
פתרון
נסמן 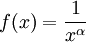 וכן
וכן 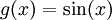 . עבור
. עבור 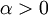 ברור כי f רציפה בקטע,
ברור כי f רציפה בקטע, 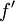 רציפה ן-f יורדת לאפס. ברור כי g רציפה. נוכיח כי G חסומה
רציפה ן-f יורדת לאפס. ברור כי g רציפה. נוכיח כי G חסומה ![\left|\int\limits_a^x\sin\right|=\left|[\cos(t)]_{t=1}^x\right|=|\cos(x)+1|\le2](/images/math/7/c/7/7c7cfa13b78e72fb2983593cdae0be90.png) . מסכנה: ממשפט דיריכלה עיבוד הנוסחה נכשל (פונקציה \matghm לא מוכרת): \int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\matghm dx
.
. מסכנה: ממשפט דיריכלה עיבוד הנוסחה נכשל (פונקציה \matghm לא מוכרת): \int\limits_1^\infty\frac{\sin(x)}{x^\alpha}\matghm dx
. 
אינטגרלים לא אמיתיים - סוג שני
במקרה זה מסתכלים בסביבה של נקודת אי-רציפות.
הגדרה: נניח f אינטגרבילית בכל תת קטע ![[\alpha,\beta]](/images/math/1/3/a/13ac621dab037fd260a54755bb2382a3.png) של
של ![(a,b]](/images/math/a/3/3/a33b8ca44ded30abf82b7dca332e9a96.png) וכן לא חסומה בסביבת a. אם קיים
וכן לא חסומה בסביבת a. אם קיים 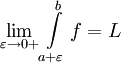 אז
אז 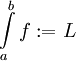 . באופן דומה מגדירים עבור גבול אינטגרציה עליון.
. באופן דומה מגדירים עבור גבול אינטגרציה עליון.
אם 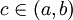 נקודת אי-רציפות נרשום
נקודת אי-רציפות נרשום 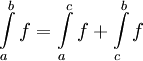 . ושוב באופן דומה לאינטגרל לא אמיתי מסוג I שני האינטגרלים צריכים להתכנס.
. ושוב באופן דומה לאינטגרל לא אמיתי מסוג I שני האינטגרלים צריכים להתכנס.
כלל ידוע: 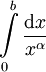 מתכנס אם"ם
מתכנס אם"ם 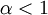 .
.
דוגמה 3
יהי 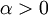 . הוכיחו כי
. הוכיחו כי 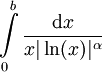 מתכנס אם"ם
מתכנס אם"ם 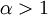 .
.
פתרון
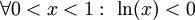 ואז
ואז 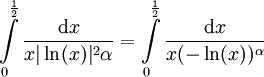 .
.
נעשה הצבה 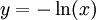 ואז
ואז 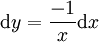 . לפיכך מספיק לפתור את האינטגרל (נסתכל תחילה על האינטגרל הלא מסויים). עבור
. לפיכך מספיק לפתור את האינטגרל (נסתכל תחילה על האינטגרל הלא מסויים). עבור 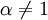 :
: 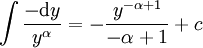 ועבור
ועבור 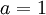 :
: 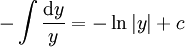 .
.
נחזור ל-x: (עבור המקרה 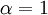 ) נקבל
) נקבל ![\int\limits_0^\frac12\frac{\mathrm dx}{x|\ln(x)|^\alpha}=[-\ln|\ln(x)||]_{x\to0+}^\frac12=\infty](/images/math/f/d/2/fd2d859ffd865b2c3ecfa7ab4f22c233.png) .
.
עבור 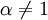 נקבל
נקבל 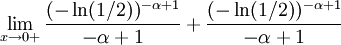 .
.
את המקרה הנ"ל החלק לשני תת מקרים:
- אם
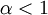 , כלומר
, כלומר 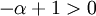 אז
אז 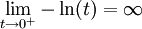 ולכן
ולכן 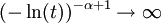 .
. - אם
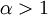 , כלומר
, כלומר 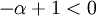 , אזי ברור כי
, אזי ברור כי 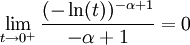 .
.

מבחן ההשוואה לאינטגרל לא אמיתי מסוג II
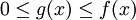 אז אם
אז אם  מתכנס גם
מתכנס גם 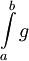 מתכנס.\
מתכנס.\
מבחן ההשוואה הגבולי
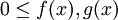 וכן
וכן 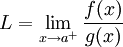 .
.
- אם
 נאמר ש-
נאמר ש- ו-
ו-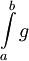 מתבדרים או מתכנסים יחדיו.
מתבדרים או מתכנסים יחדיו. - אם
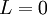 אז התכנסות
אז התכנסות 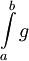 גוררת התכנסות
גוררת התכנסות  .
. - אם
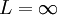 אז התכנסות
אז התכנסות  גוררת התכנסות
גוררת התכנסות 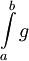 .
.
דוגמה 4
קבעו התכנסות של 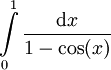 .
.
פתרון
נשווה ל-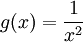 .
. 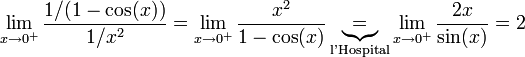 .
ידוע כי
.
ידוע כי 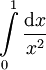 מתבדר ולכן האינטגרל הנתון מתבדר גם כן.
מתבדר ולכן האינטגרל הנתון מתבדר גם כן. 
דוגמה 5
קבעו התכנסות 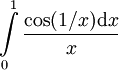 .
.
פתרון
קל לעבור מסוג II לסוג I ע"י הצבה 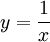 . לכן
. לכן 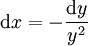 . נקבל
. נקבל 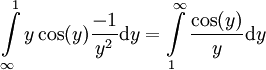 . ניתן להראות כי אינטגרל זה מתכנס בדומה למה שעשינו עם
. ניתן להראות כי אינטגרל זה מתכנס בדומה למה שעשינו עם 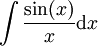 , בעזרת מבחן דיריכלה.
, בעזרת מבחן דיריכלה.
דוגמה 6
הוכיחו התכנסות בתנאי של 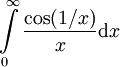 .
.
פתרון
מצאנו כבר כי 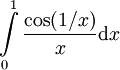 מתכנס. נותר לבדוק התכנסות בקטע
מתכנס. נותר לבדוק התכנסות בקטע 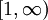 . תחילה נבדוק התכנסות בהחלט:
ברור כי
. תחילה נבדוק התכנסות בהחלט:
ברור כי 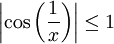 . אם רוצים להשתמש במבחן ההשוואה צריך ביטוי קטן ממנו להראות התבדרות. למשל
. אם רוצים להשתמש במבחן ההשוואה צריך ביטוי קטן ממנו להראות התבדרות. למשל 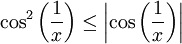 ואז
ואז 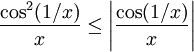 . צד שמאל מתבדר ולכן אין התכנסות בהחלט.
. צד שמאל מתבדר ולכן אין התכנסות בהחלט.
נמשיך בתרגול הבא.