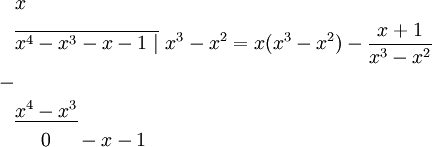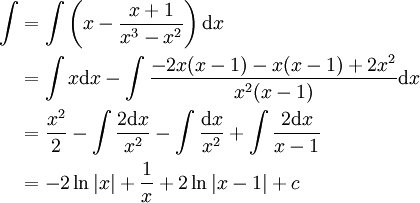משתמש:אור שחף/133 - תרגול/13.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - תרגול
תוכן עניינים
שיטות אינטגרציה (המשך)
דוגמה 0
פתור 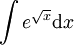 .
.
פתרון
נשתמש בשיטת ההצבה:
נציב 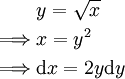
|
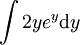
|

|
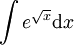
|
|||
| אינטגרציה בחלקים: | 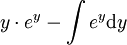
|

|
||||
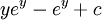
|

|
|||||
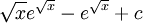
|

|

אינטגרלים של פונקציות רציונליות
נמצא אינטגרלים לפונקציות מהצורה 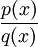 כאשר
כאשר 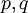 פולינומים. למשל, האינטגרלים
פולינומים. למשל, האינטגרלים 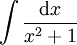 ו-
ו-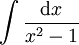 . פתרון שני האינטגרלים יכול להיות שונה כי האינטגרל הראשון אי-פריק ב-
. פתרון שני האינטגרלים יכול להיות שונה כי האינטגרל הראשון אי-פריק ב-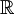 , בעוד שהשני כן פריק.
, בעוד שהשני כן פריק.
דוגמה 1
נפתור 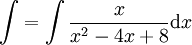 .
.
פתרון
באופן כללי, אם מעלת המונה היא n ומעלת המכנה היא n+1 נכוון ל-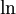 (כי
(כי 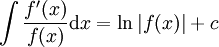 ). ואכן, אם
). ואכן, אם 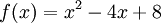 אז
אז 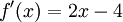 . נשנה את המונה כך שיהיה
. נשנה את המונה כך שיהיה 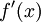 :
:
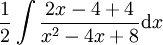
|

|
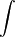
|
||||
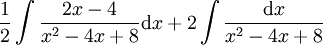
|

|
|||||
כאשר המכנה הוא פולינום אי פריק נכוון ל-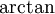 ( (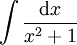 ): ):
|
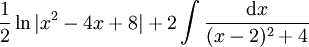
|

|
||||
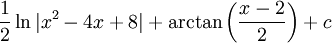
|

|

לעומת זאת, אם המכנה הוא פולינום פריק (ואנו יודעים לפרק אותו) ניתן להשתמש בשיטת "פירוק לשברים" שמטרתה להוריד את דרגת המכנה - מחפשים A,B שיקיימו 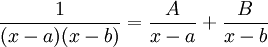 .
.
דוגמה 2
נחשב 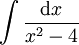 .
.
פתרון
קל לראות שהמכנה פריק ושווה ל-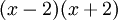 . עתה מחפשים A,B כנ"ל ומקבלים
. עתה מחפשים A,B כנ"ל ומקבלים 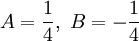 . לכן האינטגרל הוא
. לכן האינטגרל הוא 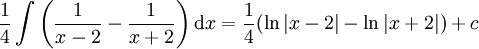 .
. 
דוגמה 3
נמצא 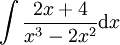 .
.
פתרון
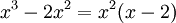 ולכן
ולכן 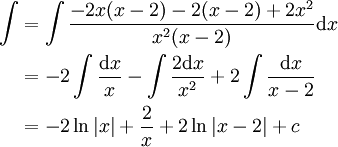

דוגמה 4
נחשב 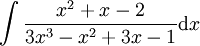 .
.
פתרון
אפשר לראות שהמכנה שווה ל-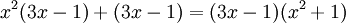 . ברור כי עבור
. ברור כי עבור 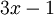 יש שורש
יש שורש  , בעוד של-
, בעוד של-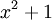 אין שורשים ממשיים. לכן יש למצוא A,B,C עבורם האינטגרנד הוא
אין שורשים ממשיים. לכן יש למצוא A,B,C עבורם האינטגרנד הוא 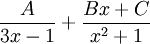 . נקבל
. נקבל 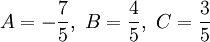 ולכן
ולכן 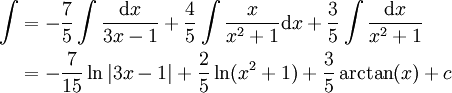

כלל: כאשר הפונקציה רציונלית ומעלת המונה גדולה מהמכנה נפנה לחילוק פולינומים.
דוגמה 5
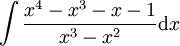
פתרון
נחלק: