הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/22.5.11"
(←אינטגרציה איבר-איבר בסדרות) |
מ (←מבחן ה-M של ווירשטראס) |
||
| שורה 21: | שורה 21: | ||
==מבחן ה-M של ווירשטראס== | ==מבחן ה-M של ווירשטראס== | ||
| − | יהי <math>\sum f_n(x)</math> טור פונקציות בקטע I. אם קיים טור | + | יהי <math>\sum f_n(x)</math> טור פונקציות בקטע I. אם קיים טור מתכנס של מספרים חיוביים <math>\sum a_n</math> כך שלכל n גדול מספיק ולכל <math>x\in I</math> מתקיים <math>|f_n(x)|\le a_n</math> אז <math>\sum f_n(x)</math> מתכנס במ"ש ב-I. |
| + | |||
==דוגמה 4== | ==דוגמה 4== | ||
הוכח כי <math>\sum_{n=1}^\infty x^n(1-x)^n</math> מתכנס במ"ש ב-<math>[0,1]</math>. | הוכח כי <math>\sum_{n=1}^\infty x^n(1-x)^n</math> מתכנס במ"ש ב-<math>[0,1]</math>. | ||
גרסה מ־19:06, 18 ביוני 2011
תוכן עניינים
התכנסות במ"ש (המשך)
משפט דיני
אם  סדרת פונקציות רציפה המוגדרת בקטע
סדרת פונקציות רציפה המוגדרת בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ומתכנסת נקודתית בקטע זה לפונקציה רציפה f. בנוסף
ומתכנסת נקודתית בקטע זה לפונקציה רציפה f. בנוסף  סדרה עולה לכל
סדרה עולה לכל ![x\in[a,b]](/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png) . אזי
. אזי  מתכנסת במ"ש ב-
מתכנסת במ"ש ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .
.
דוגמה 1
בדוק הכנסות עבור הסדרה ![f_n(x)=\sqrt[n]{\sin(x)}](/images/math/6/1/5/615da40819a44ed7f00931c4a693c793.png) בקטע
בקטע
פתרון
נישם לב שעבור x בקטע 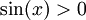 . קל לראות גם שפונקצית הגבול
. קל לראות גם שפונקצית הגבול ![\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}\sqrt[n]{\sin(x)}=1](/images/math/e/9/f/e9fa75dca80bd3466f49d47d789843b1.png) . ברור כי
. ברור כי  רציפות ובקטע מתקיים
רציפות ובקטע מתקיים ![\sqrt[n+1]{\sin(x)}\ge\sqrt[n]{\sin(x)}](/images/math/2/c/3/2c3528b548e323548058668b8d613d35.png) . ברור כי פונקציה הגבול רציפה ולכן מתקיימים תנאי משפט דיני, מכאן שההתכנסות במ"ש.
. ברור כי פונקציה הגבול רציפה ולכן מתקיימים תנאי משפט דיני, מכאן שההתכנסות במ"ש. 
פתרון
נשים לב שנתון קטע פתוח, לכן לא ניתן להשתמש בתנאי דיני. ברור לנו שפונקצית הגבול 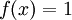 ומכיוון ש-
ומכיוון ש-![\sup_{x\in(0,\pi)}\left|1-\sqrt[n]{\sin(x)}\right|=1\ne0](/images/math/a/c/5/ac57619d7616844ec4df52447554b9ce.png) .
. 
דוגמה 2
קבעו אם הטור 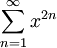 מתכנס ב-
מתכנס ב-![\left[-\frac34,\frac34\right]](/images/math/f/9/c/f9cb8580f69fec764b3cd383f7ee8ad1.png) .
.
פתרון
נשתמש בטור הנדסי, נרשום 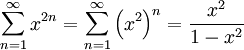 ולכן יש התכנסות לפונקציה רציפה בקטע. ברור שאיברי הטור פונקציות רציפות ואי שליליות (ולכן מתקיימת מונוטוניות). מסקנה: לפי משפט דיני ההתכנסות במ"ש.
ולכן יש התכנסות לפונקציה רציפה בקטע. ברור שאיברי הטור פונקציות רציפות ואי שליליות (ולכן מתקיימת מונוטוניות). מסקנה: לפי משפט דיני ההתכנסות במ"ש. 
דוגמה 3 משיעור קודם
הוכח או הפרך: אם ![f_n:[a,b]\to[c,d]](/images/math/4/a/9/4a9541b49b92a67090b89ac221d9bcd5.png) סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן
סדרת פונקציות המתכנסת במ"ש לפונקצית הגבול f וכן ![g:[c,d]\to\mathbb R](/images/math/4/7/e/47e54f5c5ac4f2174d7fe3833509cbd4.png) פונקציה רציפה אז
פונקציה רציפה אז 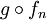 היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול
היא סדרת פונקציות המתכנסות במ"ש לפונקצית הגבול 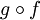 .
.
פתרון
נשים לב כי g רציפה בקטע סגור ולכן רציפה במ"ש. כלומר לכל  יש
יש 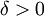 כך שאם
כך שאם 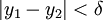 אז
אז 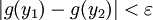 . בנוסף נתון ש-
. בנוסף נתון ש- מתכנסת במ"ש ולכן יש N כך שלכל
מתכנסת במ"ש ולכן יש N כך שלכל 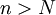 מתקיים
מתקיים 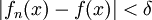 (בפרט אפשר לבחור
(בפרט אפשר לבחור 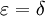 .
נשים לב ש-
.
נשים לב ש-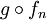 מוגדרת היטב ושם לכל
מוגדרת היטב ושם לכל 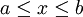 ובפרט עבור
ובפרט עבור 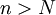 מתקיים
מתקיים 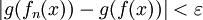 .
.
מבחן ה-M של ווירשטראס
יהי 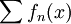 טור פונקציות בקטע I. אם קיים טור מתכנס של מספרים חיוביים
טור פונקציות בקטע I. אם קיים טור מתכנס של מספרים חיוביים 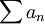 כך שלכל n גדול מספיק ולכל
כך שלכל n גדול מספיק ולכל 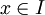 מתקיים
מתקיים 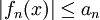 אז
אז 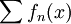 מתכנס במ"ש ב-I.
מתכנס במ"ש ב-I.
דוגמה 4
הוכח כי 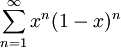 מתכנס במ"ש ב-
מתכנס במ"ש ב-![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
פתרון
נרשום את הטור כ-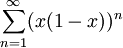 נסמן
נסמן 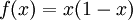 ונחסום אותה:
ונחסום אותה: 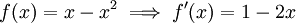 ו-
ו-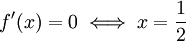 , שהיא מקסימום כי
, שהיא מקסימום כי 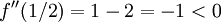 . נותר לבדוק את קצוות הקטע:
. נותר לבדוק את קצוות הקטע: ![x\in[0,1]\implies0\le x(1-x)\le\frac14\implies f_n(x)=(x(1-x))^n\le\left(\frac14\right)^n](/images/math/2/c/0/2c046b1ea348743b82a4d619594dc0fc.png) . לפי מבחן ה-M של ווירשטרס
. לפי מבחן ה-M של ווירשטרס 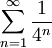 מתכנס (כי זהו טור הנדסי) ולכן מקבילים כי הטור
מתכנס (כי זהו טור הנדסי) ולכן מקבילים כי הטור 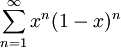 מתכנס במ"ש.
מתכנס במ"ש.
אינטגרציה איבר-איבר בסדרות
אם  סדרת פונקציות רציפות המתכנסות במ"ש. לפונקציות f בקטע I אז f אינטגרבילית בקטע ומתקיים
סדרת פונקציות רציפות המתכנסות במ"ש. לפונקציות f בקטע I אז f אינטגרבילית בקטע ומתקיים 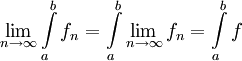
דוגמה 5
קבע האם 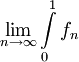 מתכנס כאשר
מתכנס כאשר 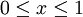 ו-
ו-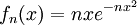 . נציב
. נציב 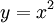 ואז
ואז ![\int\limits_0^1 f_n=\frac12\int\limits_0^1ne^{-ny}\mathrm dy=\frac12\left[\frac{ne^{-ny}}{-n}\right]_{y=0}^1=-\frac12e^{-n}+\frac12\to\frac12](/images/math/c/1/1/c11c030a7d46358eb3d199db12d92788.png) עבור צד ימין
עבור צד ימין 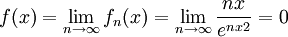 (השיוויון האחרון לפי לופיטל) ולכן ברור כי
(השיוויון האחרון לפי לופיטל) ולכן ברור כי 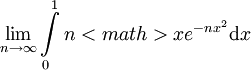 </math> ז"א אכן לא מתקיים שיוויון.
</math> ז"א אכן לא מתקיים שיוויון.
נראה ש- לא מתכנסת במ"ש.
לא מתכנסת במ"ש.
=פתרון
ברור כי פונקצית הגבול היא 0. נשתש במבחן ה-M (כי כל גישה אחרת דורשת חלוקה לקטעים). נחפש מקסימום ל-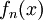 :
: 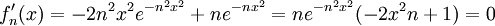 ונקבל
ונקבל 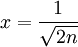 . מתקיים
. מתקיים 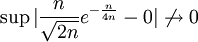 .
.
![\left[\frac\pi4,\frac34\pi\right]](/images/math/6/a/8/6a888a05d616bb2de9b623b457418224.png)