הבדלים בין גרסאות בדף "משתמש:אור שחף/133 - תרגול/29.5.11"
(←דוגמה 1) |
|||
| שורה 1: | שורה 1: | ||
=סכומי טורים= | =סכומי טורים= | ||
| − | '''תזכורת:''' (אינטגרציה איבר איבר בסדרות) אם <math>f_n</math> סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-<math>[a,b]</math>, אז f אינטגרבילית ומתקיים <math>\lim_{n\to\infty}\int\limits_a^b f_n=\int\limits_a^b f</math>. באופן דומה ננסח עבור גזירה איבר-איבר בסדרות: <math>f_n</math> סדרת פונקציות גזירות ורציפות ב-<math>[a,b]</math> המתכנסת בנקודה אחת <math>x_0\in[a,b]</math> ל-<math>f(x_0)</math>. אם <math>f_n'</math> סדרת פונקציות המתכנסות במ"ש ב-<math>[a,b]</math> אז <math>f</math> גזירה <math>\lim_{n\to\infty} f_n'(x)=f'(x)=\left(\lim_{n\to\infty}f_n(x)\right)'</math> | + | '''תזכורת:''' (אינטגרציה איבר איבר בסדרות) אם <math>f_n</math> סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-<math>[a,b]</math>, אז f אינטגרבילית ומתקיים <math>\lim_{n\to\infty}\int\limits_a^b f_n=\int\limits_a^b f</math>. באופן דומה ננסח עבור גזירה איבר-איבר בסדרות: <math>f_n</math> סדרת פונקציות גזירות ורציפות ב-<math>[a,b]</math> המתכנסת בנקודה אחת לפחות <math>x_0\in[a,b]</math> ל-<math>f(x_0)</math>. אם <math>f_n'</math> סדרת פונקציות המתכנסות במ"ש ב-<math>[a,b]</math> אז <math>f</math> גזירה <math>\lim_{n\to\infty} f_n'(x)=f'(x)=\left(\lim_{n\to\infty}f_n(x)\right)'</math>. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | יהי <math> | + | באופן דומה נגדיר עבור טורים. עבור אינטגרציה, לדוגמה: יהי <math>\sum_{n=1}^\infty f_n(x)</math> טור של פונקציות רציפות ב-<math>[a,b]</math> המתכנס במ"ש בקטע לפונקצית סכום <math>S(x)</math>, אזי טור המספרים מתכנס ומתקיים <math>\sum_{n=0}^\infty \int\limits_a^b f_n=\int\limits_a^b \sum_{n=0}^\infty=\int\limits_a^b S</math>. |
| − | + | ||
| − | + | ||
גזירה איבר איבר של טורי פונקציות: יהיו <math>f_n</math> פונציות גזירות רציפות ב-<math>[a,b]</math> כך שהטור <math>\sum_{n=0}^\infty f_n(x)</math> מתכנס ב-<math>x_0\in[a,b]</math> ל-<math>S(x_0)</math> אם טור הנגזרות <math>\sum_{n=0}^\infty f_n'(x)</math> מתכנס במידה שווה בקטע אז מתקיים <math>\sum_{n=0}^\infty f_n'(x)=S'(x)=\left(\sum_{n=0}^\infty f_n(x)\right)'</math>. | גזירה איבר איבר של טורי פונקציות: יהיו <math>f_n</math> פונציות גזירות רציפות ב-<math>[a,b]</math> כך שהטור <math>\sum_{n=0}^\infty f_n(x)</math> מתכנס ב-<math>x_0\in[a,b]</math> ל-<math>S(x_0)</math> אם טור הנגזרות <math>\sum_{n=0}^\infty f_n'(x)</math> מתכנס במידה שווה בקטע אז מתקיים <math>\sum_{n=0}^\infty f_n'(x)=S'(x)=\left(\sum_{n=0}^\infty f_n(x)\right)'</math>. | ||
| − | ==דוגמה | + | ==דוגמה 1== |
| − | <math>\sum_{n= | + | <ol> |
| + | <li> הוכיחו שלכל <math>t\in(0,1)</math> מתקיים <math>\ln(1+t)=\sum_{n=1}^\infty (-1)^{n+1}\frac{t^n}n</math>. | ||
| + | |||
===פתרון=== | ===פתרון=== | ||
| − | + | ידוע ש-<math>\ln(1+t)=\int\limits_0^t\frac{\mathrm dx}{1+x}</math> וש-<math>\frac1{1+x}=\sum_{n=0}^\infty (-1)^nx^n</math> (לפי נוסחת סכום סדרה הנדסית). מספיק להראות שהטור הנ"ל מתכנס במ"ש בקטע <math>[0,a]</math> ואז נוכל לעשות אינטגרציה איבר-איבר. נשתמש במבחן ה-M של ויירשראס: <math>|(-1)^nx^n|\le a^n</math> לכל <math>x\in[0,a]</math>. אם <math>0<a<1</math> אזי <math>\sum_{n=0}^\infty a^n</math> מתכנס ולכן <math>\sum_{n=0}^\infty (-1)^nx^n</math> מתכנס במ"ש. | |
| − | + | עתה יהי <math>t\in(0,1)</math> ונסתכל על הקטע מהצורה <math>[0,t]</math>, שם הראנו שהטור הנ"ל מתכנס במ"ש ולכן {{left|<math>\begin{align}\ln(1+t)&=\int\limits_0^t\frac{\mathrm dx}{1+x}\\&=\int\limits_0^t \sum_{n=0}^\infty (-1)^nx^n \mathrm dx\\&=\sum_{n=0}^\infty \int\limits_0^t (-1)^nx^n\mathrm dx\\&=\sum_{n=0}^\infty\left[(-1)^n\frac{x^{n+1}}{n+1}\right]_{x=0}^t\\&=\sum_{n=0}^\infty \frac{(-1)^nt^{n+1}}{n+1}\\&=\sum_{n=1}^\infty(-1)^{n+1}\frac{t^n}n\end{align}</math>}}{{משל}} | |
| − | <math> | + | </li> |
| + | <li> חשבו <math>\sum_{n=1}^\infty (-1)^n \frac1{2^nn}</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
===פתרון=== | ===פתרון=== | ||
| − | + | נעזר בסעיף 1. ברור כי <math>t=\frac12</math> נמצא בקטע <math>(0,1)</math>, ולכן נציב: <math>\sum_{n=1}^\infty\frac{(-1)^n}{2^nn}=-\sum_{n=1}^\infty(-1)^{n+1}\frac{\left(\frac12\right)^n}n=-\ln\left(1\tfrac12\right)</math>. {{משל}} | |
| + | </li> | ||
| + | </ol> | ||
| − | + | ==דוגמה 2== | |
| + | יטופל בהמשך: | ||
| + | <div style="opacity:0.5;"> | ||
| + | חשבו את סכום הטור <math>\sum_{n=1}^\infty\frac n{(n+1)x^n}</math> עבור <math>x>1</math>. | ||
| − | + | ===פתרון=== | |
| + | ראשית נוכיח שהטור <math>\sum_{n=1}^\infty x^n</math> מתכנס במ"ש ב-<math>(0,1)</math>. יהי <math>0<x_0<1</math> ולכן <math>\left|x^n\right|\le x_0^n</math> לכל <math>\frac1x\in[0,x_0]</math>. כמו כן <math>\sum_{n=1}^\infty x_0^n</math> מתכנס כי <math>0<x_0<1</math> והטור הנדסי, לכן, ממבחן ה-M של ויירשטראס, הטור <math>\sum_{n=1}^\infty x^n=\frac1{1-x}</math> מתכנס במ"ש ב-<math>[0,x_0]</math>. עתה נוכל לעשות אינטגרציה איבר-איבר: <math>\int\limits_0^x\frac{\mathrm dt}{1-t}=\int\limits_0^x\sum_{n=1}^\infty t^n\mathrm dt=\sum_{n=1}^\infty\int\limits_0^x t^n\mathrm dt=\sum_{n=2}^\infty\frac{x^{n+1}}{n+1}</math>. כמו כן, ברור כי <math>\int\limits_0^x\frac{\mathrm dt}{1-t}=[-\ln(1-t)]_{t=0}^x=-\ln(1-x)</math>. נשאר לחלק ב-x ואז לגזור. | ||
| + | </div> | ||
| − | |||
| − | |||
==דוגמה 3== | ==דוגמה 3== | ||
| − | + | מהו סכום הטור <math>\sum_{n=1}^\infty\frac n{x^n}</math> עבור <math>x<1</math>? | |
| + | |||
===פתרון=== | ===פתרון=== | ||
| − | + | נשים לב שאם נגדיר<math>f_n(x)=\frac1{x^n}</math> אזי <math>f_n'(x)=(x^{-n})'=-n\cdot x^{-n-1}=\frac{-n}{x^{n+1}}</math>. כמו כן <math>\sum_{n=1}^\infty f_n(x)=\sum_{n=1}^\infty \frac1{x^n}=\frac{1/x}{1-1/x}=\frac1{x-1}</math>. נבדוק את התנאים לגזירה איבר-איבר. דרוש ש-<math>\sum f_n'(x)</math> יתכנס במ"ש. | |
| + | |||
| + | נעזר במבחן ה-M של ויירשראס. אם <math>x>1</math> אז יש <math>1<a<x</math> שם מתקיים <math>\left|\frac{-n}{x^{n+1}}\right|\le\frac n{a^{n+1}}</math>. הטור <math>\sum_{n=1}^\infty \frac n{a^{n+1}}</math> טור מתכנס עפ"י מבחן המנה של ד'לאמר (או מבחן השורש של קושי). | ||
| + | |||
| + | נסיק שהטור <math>\sum_{n=1}^\infty\frac{-n}{x^{n+1}}</math> מתכנס במ"ש ולכן <math>\left(\sum_{n=1}^\infty \frac1{x^n}\right)'=\sum_{n=1}^\infty \left(\frac1{x^n}\right)'=\sum_{n=1}^\infty \frac{-n}{x^{n+1}}</math> וגם <math>\left(\sum_{n=1}^\infty \frac1{x^n}\right)'=\left(\frac1{x-1}\right)'=\frac{-1}{(x-1)^2}</math>. לסיכום <math>\sum_{n=1}^\infty \frac{-n}{x^{n+1}}=\frac{-1}{(x-1)^2}</math>, ולפיכך <math>\sum_{n=1}^\infty\frac n{x^n}=\frac x{(x-1)^2}</math>. {{משל}} | ||
| + | |||
| + | =טורי חזקות= | ||
| + | רדיוס ההתכנסות של טור חזקות <math>\sum_{n=1}^\infty a_nx^n</math> הוא <math>R=\frac1{\displaystyle\limsup_{n\to\infty}\sqrt[n]{|a_n|}}</math>, והוא מתכנס בהחלט ב-<math>(x_0-R,x_0+R)</math>. לגבי התכנסות בקצוות הקטע, יש לבדוק בנפרד. | ||
| − | |||
==דוגמה 4== | ==דוגמה 4== | ||
| − | + | מצאו את תחום התכנסות של הטור <math>\sum_{n=1}^\infty\frac{x^n}\sqrt[3]n</math>. | |
| + | |||
| + | ===פתרון=== | ||
| + | אכן מדובר על טור חזקות כי כאשר המקדם הכללי הוא <math>a_n=\frac1\sqrt[3]n</math>. לכן רדיוס ההתכנסות הוא <math>R=\frac1{\displaystyle\limsup_{n\to\infty}\sqrt[n]\tfrac1\sqrt[3]n}=\left(1/\limsup_{n\to\infty}\sqrt[n]n\right)^{-3}=1</math>. ז"א כאשר <math>|x|<1</math> הטור מתכנס. נשאר לבדוק האם יש התכנסות בקצוות <math>x=\pm1</math>. עבור <math>x=1</math> הטור הוא <math>\sum_{n=1}^\infty \frac{1^n}\sqrt[3]n</math>, שמתבדר כי הוא גדול מ-<math>\sum_{n=1}^\infty\frac1n=\infty</math>. עבור <math>x=-1</math> ברור שהטור מתכנס, לפי משפט לייבניץ. לסיכום, תחום ההתכנסות הוא <math>[-1,1)</math>. {{משל}} | ||
| + | |||
| + | ==דוגמה 5== | ||
| + | מצאו את תחום ההתכנסות של <math>\sum_{n=0}^\infty n!x^{n!}</math>. | ||
| + | |||
| + | ===פתרון=== | ||
| + | נשים לב כי הטור הנתון אינו טור חזקות, ולכן "נתקן" אותו. נגדיר <math>a_n=\begin{cases}n&\exists k:\ n=k!\\0&\text{else}\end{cases}</math>. נקבל את הטור <math>\sum_{n=0}^\infty a_n x^n</math>. נשים לב שאכן במקרה הזה נצטרך לחשב <math>\limsup</math> (ולא סתם <math>\lim</math>). <math>1/\limsup_{n\to\infty}\sqrt[n]{a_n}=1/\lim_{n\to\infty}\sqrt[n]n=1/1=1</math> ולכן רדיוס ההתכנסות הוא 1. נבדוק בקצוות: ב-1 הטור הוא <math>\sum_{n=0}^\infty n!\cdot 1^{n!}\to\infty</math>. עבור <math>x=-1</math> הטור הוא <math>\sum_{n=0}^\infty n!(-1)^{n!}</math>, שגם שואף לאינסוף כי <math>n!</math> זוגי לכל <math>n>1</math>. לסיכום, תחום ההתכנסות הוא <math>(-1,1)</math>. {{משל}} | ||
גרסה מ־14:55, 1 ביולי 2011
תוכן עניינים
סכומי טורים
תזכורת: (אינטגרציה איבר איבר בסדרות) אם  סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-
סדרת פונקציות רציפות המתכנסות במ"ש לפונקציה f ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , אז f אינטגרבילית ומתקיים
, אז f אינטגרבילית ומתקיים 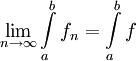 . באופן דומה ננסח עבור גזירה איבר-איבר בסדרות:
. באופן דומה ננסח עבור גזירה איבר-איבר בסדרות:  סדרת פונקציות גזירות ורציפות ב-
סדרת פונקציות גזירות ורציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המתכנסת בנקודה אחת לפחות
המתכנסת בנקודה אחת לפחות ![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) ל-
ל-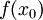 . אם
. אם 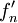 סדרת פונקציות המתכנסות במ"ש ב-
סדרת פונקציות המתכנסות במ"ש ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אז
אז  גזירה
גזירה 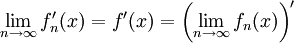 .
.
באופן דומה נגדיר עבור טורים. עבור אינטגרציה, לדוגמה: יהי 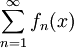 טור של פונקציות רציפות ב-
טור של פונקציות רציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) המתכנס במ"ש בקטע לפונקצית סכום
המתכנס במ"ש בקטע לפונקצית סכום 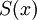 , אזי טור המספרים מתכנס ומתקיים
, אזי טור המספרים מתכנס ומתקיים 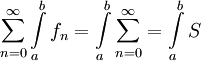 .
.
גזירה איבר איבר של טורי פונקציות: יהיו  פונציות גזירות רציפות ב-
פונציות גזירות רציפות ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) כך שהטור
כך שהטור 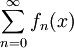 מתכנס ב-
מתכנס ב-![x_0\in[a,b]](/images/math/0/2/5/0256d46865eafa8df913009bb4f1d987.png) ל-
ל-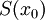 אם טור הנגזרות
אם טור הנגזרות 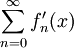 מתכנס במידה שווה בקטע אז מתקיים
מתכנס במידה שווה בקטע אז מתקיים 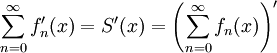 .
.
דוגמה 1
- הוכיחו שלכל
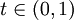 מתקיים
מתקיים 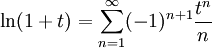 .
.
פתרון
ידוע ש-
עתה יהי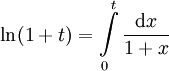 וש-
וש-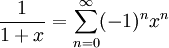 (לפי נוסחת סכום סדרה הנדסית). מספיק להראות שהטור הנ"ל מתכנס במ"ש בקטע
(לפי נוסחת סכום סדרה הנדסית). מספיק להראות שהטור הנ"ל מתכנס במ"ש בקטע ![[0,a]](/images/math/1/3/5/13596d6674a86fdafa24c4c414033e58.png) ואז נוכל לעשות אינטגרציה איבר-איבר. נשתמש במבחן ה-M של ויירשראס:
ואז נוכל לעשות אינטגרציה איבר-איבר. נשתמש במבחן ה-M של ויירשראס: 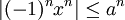 לכל
לכל ![x\in[0,a]](/images/math/a/2/e/a2e0a7db6b58ff7d7b743cc581bf12b3.png) . אם
. אם 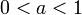 אזי
אזי 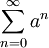 מתכנס ולכן
מתכנס ולכן 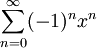 מתכנס במ"ש.
מתכנס במ"ש.
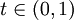 ונסתכל על הקטע מהצורה
ונסתכל על הקטע מהצורה ![[0,t]](/images/math/2/1/b/21b8fce671acf5fa4690193ad7ef3461.png) , שם הראנו שהטור הנ"ל מתכנס במ"ש ולכן
, שם הראנו שהטור הנ"ל מתכנס במ"ש ולכן ![\begin{align}\ln(1+t)&=\int\limits_0^t\frac{\mathrm dx}{1+x}\\&=\int\limits_0^t \sum_{n=0}^\infty (-1)^nx^n \mathrm dx\\&=\sum_{n=0}^\infty \int\limits_0^t (-1)^nx^n\mathrm dx\\&=\sum_{n=0}^\infty\left[(-1)^n\frac{x^{n+1}}{n+1}\right]_{x=0}^t\\&=\sum_{n=0}^\infty \frac{(-1)^nt^{n+1}}{n+1}\\&=\sum_{n=1}^\infty(-1)^{n+1}\frac{t^n}n\end{align}](/images/math/4/e/f/4ef60b9f400198b8b29e74c63907064c.png)

- חשבו
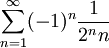 .
.
פתרון
נעזר בסעיף 1. ברור כי
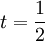 נמצא בקטע
נמצא בקטע 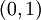 , ולכן נציב:
, ולכן נציב: 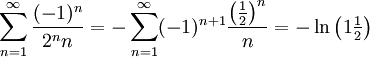 .
. 
דוגמה 2
יטופל בהמשך:
חשבו את סכום הטור 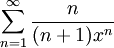 עבור
עבור 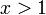 .
.
פתרון
ראשית נוכיח שהטור 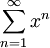 מתכנס במ"ש ב-
מתכנס במ"ש ב-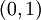 . יהי
. יהי 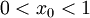 ולכן
ולכן 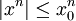 לכל
לכל ![\frac1x\in[0,x_0]](/images/math/6/a/5/6a55bd40b197ff7cddab58a71ce6cec8.png) . כמו כן
. כמו כן 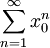 מתכנס כי
מתכנס כי 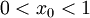 והטור הנדסי, לכן, ממבחן ה-M של ויירשטראס, הטור
והטור הנדסי, לכן, ממבחן ה-M של ויירשטראס, הטור 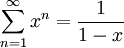 מתכנס במ"ש ב-
מתכנס במ"ש ב-![[0,x_0]](/images/math/f/2/2/f2227e7e0241f4841a3357fb19432306.png) . עתה נוכל לעשות אינטגרציה איבר-איבר:
. עתה נוכל לעשות אינטגרציה איבר-איבר: 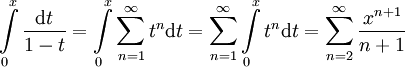 . כמו כן, ברור כי
. כמו כן, ברור כי ![\int\limits_0^x\frac{\mathrm dt}{1-t}=[-\ln(1-t)]_{t=0}^x=-\ln(1-x)](/images/math/e/1/d/e1d416857e79ea8767de68296e4c0601.png) . נשאר לחלק ב-x ואז לגזור.
. נשאר לחלק ב-x ואז לגזור.
דוגמה 3
מהו סכום הטור 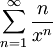 עבור
עבור 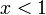 ?
?
פתרון
נשים לב שאם נגדיר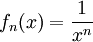 אזי
אזי 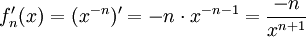 . כמו כן
. כמו כן 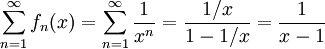 . נבדוק את התנאים לגזירה איבר-איבר. דרוש ש-
. נבדוק את התנאים לגזירה איבר-איבר. דרוש ש-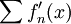 יתכנס במ"ש.
יתכנס במ"ש.
נעזר במבחן ה-M של ויירשראס. אם 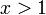 אז יש
אז יש 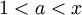 שם מתקיים
שם מתקיים 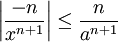 . הטור
. הטור 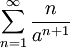 טור מתכנס עפ"י מבחן המנה של ד'לאמר (או מבחן השורש של קושי).
טור מתכנס עפ"י מבחן המנה של ד'לאמר (או מבחן השורש של קושי).
נסיק שהטור 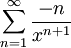 מתכנס במ"ש ולכן
מתכנס במ"ש ולכן 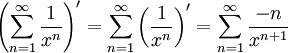 וגם
וגם 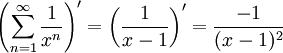 . לסיכום
. לסיכום 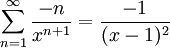 , ולפיכך
, ולפיכך 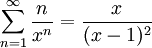 .
. 
טורי חזקות
רדיוס ההתכנסות של טור חזקות 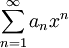 הוא
הוא ![R=\frac1{\displaystyle\limsup_{n\to\infty}\sqrt[n]{|a_n|}}](/images/math/4/5/b/45baae0aacfd1793f8d98ef6d5320503.png) , והוא מתכנס בהחלט ב-
, והוא מתכנס בהחלט ב-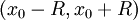 . לגבי התכנסות בקצוות הקטע, יש לבדוק בנפרד.
. לגבי התכנסות בקצוות הקטע, יש לבדוק בנפרד.
דוגמה 4
מצאו את תחום התכנסות של הטור ![\sum_{n=1}^\infty\frac{x^n}\sqrt[3]n](/images/math/0/0/7/00747b6a93f81bbd01d80dda37a6d9d4.png) .
.
פתרון
אכן מדובר על טור חזקות כי כאשר המקדם הכללי הוא ![a_n=\frac1\sqrt[3]n](/images/math/7/7/1/771016d00f8faecaca4a1ffb64761bb9.png) . לכן רדיוס ההתכנסות הוא
. לכן רדיוס ההתכנסות הוא ![R=\frac1{\displaystyle\limsup_{n\to\infty}\sqrt[n]\tfrac1\sqrt[3]n}=\left(1/\limsup_{n\to\infty}\sqrt[n]n\right)^{-3}=1](/images/math/d/1/1/d118e915a18caf023be4a4241876a062.png) . ז"א כאשר
. ז"א כאשר 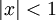 הטור מתכנס. נשאר לבדוק האם יש התכנסות בקצוות
הטור מתכנס. נשאר לבדוק האם יש התכנסות בקצוות 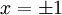 . עבור
. עבור 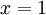 הטור הוא
הטור הוא ![\sum_{n=1}^\infty \frac{1^n}\sqrt[3]n](/images/math/d/2/3/d23bec4b81c53df7fc40520549ae1fce.png) , שמתבדר כי הוא גדול מ-
, שמתבדר כי הוא גדול מ-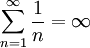 . עבור
. עבור 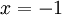 ברור שהטור מתכנס, לפי משפט לייבניץ. לסיכום, תחום ההתכנסות הוא
ברור שהטור מתכנס, לפי משפט לייבניץ. לסיכום, תחום ההתכנסות הוא 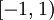 .
. 
דוגמה 5
מצאו את תחום ההתכנסות של 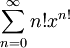 .
.
פתרון
נשים לב כי הטור הנתון אינו טור חזקות, ולכן "נתקן" אותו. נגדיר 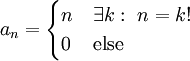 . נקבל את הטור
. נקבל את הטור 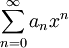 . נשים לב שאכן במקרה הזה נצטרך לחשב
. נשים לב שאכן במקרה הזה נצטרך לחשב 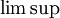 (ולא סתם
(ולא סתם 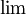 ).
). ![1/\limsup_{n\to\infty}\sqrt[n]{a_n}=1/\lim_{n\to\infty}\sqrt[n]n=1/1=1](/images/math/b/a/f/bafba899c239badb2ac8a4e7ffece6c5.png) ולכן רדיוס ההתכנסות הוא 1. נבדוק בקצוות: ב-1 הטור הוא
ולכן רדיוס ההתכנסות הוא 1. נבדוק בקצוות: ב-1 הטור הוא 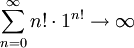 . עבור
. עבור 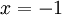 הטור הוא
הטור הוא 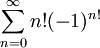 , שגם שואף לאינסוף כי
, שגם שואף לאינסוף כי 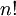 זוגי לכל
זוגי לכל 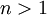 . לסיכום, תחום ההתכנסות הוא
. לסיכום, תחום ההתכנסות הוא 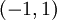 .
. 