פתרון
תרגיל 1
יהיו  ו-
ו- קבוצות סופיות בעלות עוצמה זהה. הוכיחו שכל פונקציה מ-
קבוצות סופיות בעלות עוצמה זהה. הוכיחו שכל פונקציה מ- ל-
ל- הינה על אם"ם היא חח"ע.
פתרון:\
נסמן
הינה על אם"ם היא חח"ע.
פתרון:\
נסמן 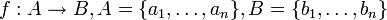 . כאשר כל האיברים ב-
. כאשר כל האיברים ב- שונים זה מזה וכנ"ל ב-
שונים זה מזה וכנ"ל ב- .
.
נניח  חח"ע אזי
חח"ע אזי 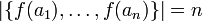 כיוון ש-
כיוון ש-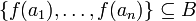 ובשניהם יש אותו מספר איברים, מתקיים שיוון ולכן
ובשניהם יש אותו מספר איברים, מתקיים שיוון ולכן  על.
על.
נניח  על. נניח בשלילה ש-
על. נניח בשלילה ש- אינה חח"ע אזי
אינה חח"ע אזי 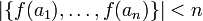 (כי יש שני איברים שנשלחים לאותו מקום) ואז
(כי יש שני איברים שנשלחים לאותו מקום) ואז  אינה על, שזו סתירה.
אינה על, שזו סתירה.
הערה: הדבר אינו נכון אם  ו-
ו- קבוצות אינסופיות. נסו למצוא דוגמה.
קבוצות אינסופיות. נסו למצוא דוגמה.
תרגיל 2
תהא  קבוצה. נגדיר פונקציה
קבוצה. נגדיר פונקציה 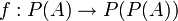 ע"י:
ע"י: 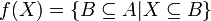 האם היא חח"ע? על?
פתרון:
חח"ע: כן. תהיינה
האם היא חח"ע? על?
פתרון:
חח"ע: כן. תהיינה 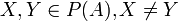 אם
אם 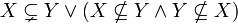 אזי
אזי 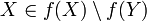 . אחרת
. אחרת 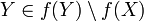 . כלומר
. כלומר 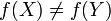 .
.
על: לא. נבחר 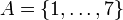 . למשל לקבוצה
. למשל לקבוצה 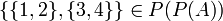 אין מקור. אין תת קבוצה שהאוסף הזה הוא בדיוק אוסף הקבוצות המכילות אותה.
אין מקור. אין תת קבוצה שהאוסף הזה הוא בדיוק אוסף הקבוצות המכילות אותה.
תרגיל 3
יהיו 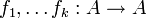 שכולן הפיכות\חח"ע\על. הוכיחו שההרכבה
שכולן הפיכות\חח"ע\על. הוכיחו שההרכבה 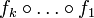 הפיכה\חח"ע\על.
פתרון:
למעשה אפשר לעשות אינדוקציה על המשפט מן ההרצאה. עבור שתי פונקציות זה בהרצאה. נניח נכונות ל
הפיכה\חח"ע\על.
פתרון:
למעשה אפשר לעשות אינדוקציה על המשפט מן ההרצאה. עבור שתי פונקציות זה בהרצאה. נניח נכונות ל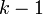 ונוכיח ל
ונוכיח ל .
.
חח"ע: נניח 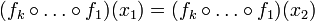 אזי מחח"ע של
אזי מחח"ע של 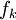 נקבל כי
נקבל כי 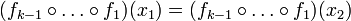 מהנחת האינדוקציה עבור
מהנחת האינדוקציה עבור 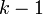 פונקציות נקבל שההרכבה חח"ע ולכן
פונקציות נקבל שההרכבה חח"ע ולכן 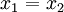 .
.
על: יהא 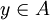 כיוון ש-
כיוון ש-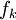 על, קיים
על, קיים 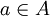 כך ש-
כך ש-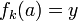 .
בנוסף, מהנחת האינדוקציה קיים
.
בנוסף, מהנחת האינדוקציה קיים 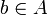 כך ש
כך ש 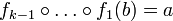 ולכן נקבל
ולכן נקבל
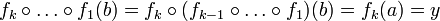 . מש"ל.
. מש"ל.
הפיכות: נובע מחח"ע יחד עם על.