הבדלים בין גרסאות בדף "פתרון אינפי 1, תשנ"ט, מועד ב,"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(יצירת דף עם התוכן "1) היה בתרגול (אוהד פתר), אך לא מופיע במערכי התרגול. לכן אעתיק את הפתרון לכאן: א) נניח ש<math>\sum^{...")
 
שורה 3: שורה 3:
 
א) נניח ש<math>\sum^{\infty } b_n</math> מתכנס. נפעיל את מבחן העיבוי -לכן <math>\sum^{\infty } 2^nb_{2^n}</math> מתכנס, ולפי התנאי ההכרחי זה גורר ש <math>2^nb_{2^n}\rightarrow 0</math>.
 
א) נניח ש<math>\sum^{\infty } b_n</math> מתכנס. נפעיל את מבחן העיבוי -לכן <math>\sum^{\infty } 2^nb_{2^n}</math> מתכנס, ולפי התנאי ההכרחי זה גורר ש <math>2^nb_{2^n}\rightarrow 0</math>.
  
−
לכל n קיים k כך ש- <math>2^k\leq n <2^{k+1} </math> (טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת <math>k=\lfloor  log_2{n} \right \rfloor</math>).
+
לכל n קיים k כך ש- <math>2^k\leq n <2^{k+1} </math> (טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת <math> k=\left \lfloor  log_2{n} \right \rfloor</math>).
  
 
הסדרה <math>\left \{ b_n \right \}</math> יורדת ולכן <math>x<y\rightarrow b_x>b_y</math>.
 
הסדרה <math>\left \{ b_n \right \}</math> יורדת ולכן <math>x<y\rightarrow b_x>b_y</math>.
שורה 13: שורה 13:
 
נשתמש שוב בתוצאה האלגברית: <math>0\leftarrow \frac{1}{2}2^{k+1}b_{2^{k+1}}=2^kb_{2^{k+1}}\leq nb_{2^{k+1}}\leq nb_n \leq nb_{2^k}\leq 2^{k+1}b_{2^k}\rightarrow 0</math>\
 
נשתמש שוב בתוצאה האלגברית: <math>0\leftarrow \frac{1}{2}2^{k+1}b_{2^{k+1}}=2^kb_{2^{k+1}}\leq nb_{2^{k+1}}\leq nb_n \leq nb_{2^k}\leq 2^{k+1}b_{2^k}\rightarrow 0</math>\
  
−
ולכן לפי משפט הסנדוויץ' נקבל את הדרוש - <math>nb_b\rightarrow 0</math>.
+
ולכן לפי משפט הסנדוויץ' נקבל את הדרוש, <math>nb_b\rightarrow 0</math>.
  
 
ב) דוגמה נגדית: <math>b_n=\frac{1}{n\cdot ln(n)}</math>. ממבחן העיבוי הטור <math>\sum b_n</math> מתבדר, אך בכל זאת <math>nb_n=\frac{1}{ ln(n)}\rightarrow 0</math>.
 
ב) דוגמה נגדית: <math>b_n=\frac{1}{n\cdot ln(n)}</math>. ממבחן העיבוי הטור <math>\sum b_n</math> מתבדר, אך בכל זאת <math>nb_n=\frac{1}{ ln(n)}\rightarrow 0</math>.
שורה 27: שורה 27:
 
2)א) נבדוק התכנסות בהחלט: ברור שהטור <math>\sum cos(\frac{1}{n})</math> מתבדר לפי התנאי ההכרחי, שכן <math>\lim_{n \to \infty }cos(\frac{1}{n})=cos0=1</math> שונה מ0.
 
2)א) נבדוק התכנסות בהחלט: ברור שהטור <math>\sum cos(\frac{1}{n})</math> מתבדר לפי התנאי ההכרחי, שכן <math>\lim_{n \to \infty }cos(\frac{1}{n})=cos0=1</math> שונה מ0.
  
−
הטור מתכנס בתנאי לפי מבחן לייבניץ.
+
הטור מתבדר לפי התנאי ההכרחי. (כי <math>\lim_{n \to \infty }a_n=0\leftrightarrow \lim_{n \to \infty }(-1)^na_n=0</math>)
  
−
ב)
+
ב) נבדוק התכנסות בהחלט: <math>\sum \begin{pmatrix}
 +
2n\\
 +
n
 +
\end{pmatrix}\frac{1}{2^{3n}}=:\sum a_n</math>. נוכיח התכנסות בהחלט ע"י שימוש במבחן המנה:
 +
 
 +
<math>\frac{a_{n+1}}{a_n}= \begin{pmatrix}
 +
2n+2\\
 +
n+1
 +
\end{pmatrix}\frac{1}{2^{3n+3}}\cdot \frac{2^{3n}}{\begin{pmatrix}
 +
2n\\
 +
n
 +
\end{pmatrix}}=</math>
 +
 
 +
<math>=\frac{(2n+2)!}{(n+1)!^2}\cdot \frac{n!^2}{(2n)!\cdot 2^3}=\frac{(2n+2)!}{(n+1)^2}\cdot \frac{1}{8(2n)!}=\frac{(2n+1)(2n+2)}{8(n+1)^2}=\frac{2n+1}{4n+4}
 +
</math>
 +
 
 +
 
 +
נעבור לגבול: <math>\lim_{n \to \infty }\frac{a_{n+1}}{a_n}=\lim_{n \to \infty }\frac{2n+1}{4n+4}=\frac{1}{2}<1</math>, לכן הטור מתכנס בהחלט, ובפרט מתכנס.

גרסה מ־07:32, 2 בפברואר 2012

1) היה בתרגול (אוהד פתר), אך לא מופיע במערכי התרגול. לכן אעתיק את הפתרון לכאן:

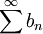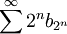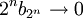א) נניח ש\sum^{\infty } b_n מתכנס. נפעיל את מבחן העיבוי -לכן \sum^{\infty } 2^nb_{2^n} מתכנס, ולפי התנאי ההכרחי זה גורר ש 2^nb_{2^n}\rightarrow 0.

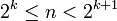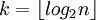לכל n קיים k כך ש- 2^k\leq n <2^{k+1} (טענה אלגברית, אין צורך להוכיח - אבל נדמה לי שישירות אפשר לקחת k=\left \lfloor log_2{n} \right \rfloor).

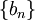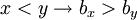הסדרה \left \{ b_n \right \} יורדת ולכן x<y\rightarrow b_x>b_y.

נפעיל נימוק זה על התוצאה שקיבלנו, ונקבל ש 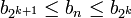b_{2^{k+1}}\leq b_n \leq b_{2^k}.

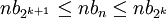
נכפיל בn (חיובי) את אגפי האי-שוויון: nb_{2^{k+1}}\leq nb_n \leq nb_{2^k}

נשתמש שוב בתוצאה האלגברית: 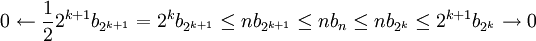0\leftarrow \frac{1}{2}2^{k+1}b_{2^{k+1}}=2^kb_{2^{k+1}}\leq nb_{2^{k+1}}\leq nb_n \leq nb_{2^k}\leq 2^{k+1}b_{2^k}\rightarrow 0\

ולכן לפי משפט הסנדוויץ' נקבל את הדרוש, 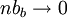nb_b\rightarrow 0.

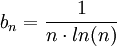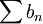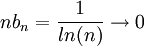ב) דוגמה נגדית: b_n=\frac{1}{n\cdot ln(n)}. ממבחן העיבוי הטור \sum b_n מתבדר, אך בכל זאת nb_n=\frac{1}{ ln(n)}\rightarrow 0.

ג) ניקח את הסדרה 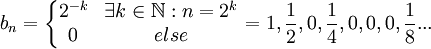b_n=\left\{\begin{matrix} 2^{-k} &\exists k \in \mathbb{N}:n=2^k \\ 0 & else \end{matrix}\right.=1,\frac{1}{2},0,\frac{1}{4},0,0,0,\frac{1}{8}....

הטור 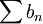\sum b_n מתכנס (טור גיאומטרי עם אפסים שלא משפיעים), אבל בכל זאת 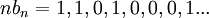nb_n=1,1,0,1,0,0,0,1... אינו מתכנס שכן יש לו תת סדרה ששווה 1 ובפרט שואפת לאחת (וידוע שאם סדרה מתכנסת לגבול אז גם כל תת סדרה שלה מתכנסת אליו).


2)א) נבדוק התכנסות בהחלט: ברור שהטור 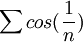\sum cos(\frac{1}{n}) מתבדר לפי התנאי ההכרחי, שכן 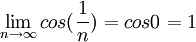\lim_{n \to \infty }cos(\frac{1}{n})=cos0=1 שונה מ0.

הטור מתבדר לפי התנאי ההכרחי. (כי 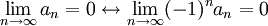\lim_{n \to \infty }a_n=0\leftrightarrow \lim_{n \to \infty }(-1)^na_n=0)

ב) נבדוק התכנסות בהחלט: 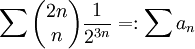\sum \begin{pmatrix} 2n\\ n \end{pmatrix}\frac{1}{2^{3n}}=:\sum a_n. נוכיח התכנסות בהחלט ע"י שימוש במבחן המנה:

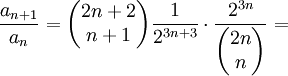
\frac{a_{n+1}}{a_n}= \begin{pmatrix} 2n+2\\ n+1 \end{pmatrix}\frac{1}{2^{3n+3}}\cdot \frac{2^{3n}}{\begin{pmatrix} 2n\\ n \end{pmatrix}}=

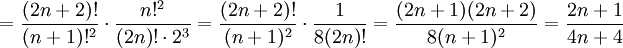
=\frac{(2n+2)!}{(n+1)!^2}\cdot \frac{n!^2}{(2n)!\cdot 2^3}=\frac{(2n+2)!}{(n+1)^2}\cdot \frac{1}{8(2n)!}=\frac{(2n+1)(2n+2)}{8(n+1)^2}=\frac{2n+1}{4n+4}


נעבור לגבול: 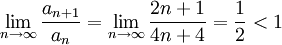\lim_{n \to \infty }\frac{a_{n+1}}{a_n}=\lim_{n \to \infty }\frac{2n+1}{4n+4}=\frac{1}{2}<1, לכן הטור מתכנס בהחלט, ובפרט מתכנס.

מקור: https://math-wiki.com/index.php?title=פתרון_אינפי_1,_תשנ%22ט,_מועד_ב,&oldid=19245