פתרון לינארית 2, אונ' בר אילן, תש"ע, מועד ב', שאלה 1

הוכח כי המטריצות הממשיות הבאות דומות: 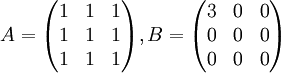$A=\begin{pmatrix} 1 &1 &1 \\ 1 &1 &1 \\ 1 & 1 & 1 \end{pmatrix}, B=\begin{pmatrix} 3 &0 & 0\\ 0 & 0 &0 \\ 0&0 & 0 \end{pmatrix}$

נוכיח כי למטריצות הבאות אותה צורת ג'ורדן, ומזה ינבע שהן דומות זו לזו. נתחיל ב$A$.

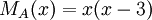נחשב את הפולינום האופייני של $A$: P_{A}(x)=\begin{vmatrix} x-1 &-1 &-1 \\ -1 & x-1 & -1\\ -1 & -1 & x-1 \end{vmatrix}=(x-1)^{3}-1-1-((x-1)+(x-1)+(x-1))=x^{3}-3x^{2}=x^{2}(x-3) והפולינום המינימלי שלו הוא $M_{A}(x)=x(x-3)$ ולכן צורת הג'ורדן היא 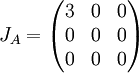$J_{A}=\begin{pmatrix} 3 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}$ שכן מס' הפעמים שמופיע הערך 3 הוא 1, ומספר הפעמים שמופיע הערך 0 הוא 2, אך הבלוק הגדול ביותר של 0 הוא מסדר 1, ולכן קבלנו את המטריצה הנ"ל.

נחשב את הפולינום האופייני של B: 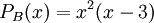$P_{B}(x)=x^{2}(x-3)$ והפולינום המינימלי הוא 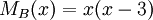$M_{B}(x)=x(x-3)$ ולכן נקבל שגם כאן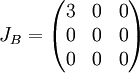 $J_{B}=\begin{pmatrix} 3 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}$

ובסה"כ קבלנו שלשתי המטריצות אותה צורת ג'ורדן ולכן הן דומות. מ.ש.ל.