פתרון לינארית 2, אונ' בר אילן, תשנ"א, מועד ב, שאלה 4
מתוך Math-Wiki
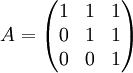
נמצא פ"א: 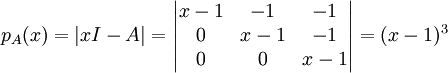 כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
כי דטר' של מטר' משולשית היא מכפלת איברי האלכסון.
זהו גם הפ"מ של A:
הפ"מ מחלק את הפ"א, לכן הפ"מ חייב להיות מהצורה 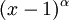 , כאשר
, כאשר 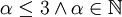 .
.
נבדוק ישירות שA-I בריבוע שונה ממטריצת אפסים: 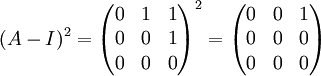
אבל 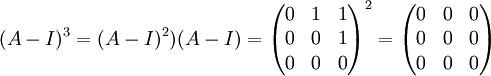
קיבלנו שהמטריצה 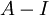 נילפ' מאינדקס 3. לכן, לפי משפט שהוכחנו, הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש
נילפ' מאינדקס 3. לכן, לפי משפט שהוכחנו, הבלוק הגדול ביותר בצורת ז'ורדן שדומה לה הוא מסדר 3=אינדקס הנילפוטנטיות.
אבל המטר' היא כבר מסדר 3, ולכן בלוק זה חייב להיות הבלוק היחיד במטריצה. קיבלנו ש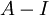 דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
דומה לבלוק ז'ורדן נילפוטנטי מסדר 3.
לפי הגדרת דמיון המטריצות, קיימת מטר' הפיכה 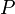 כך ש:
כך ש:
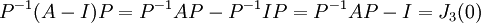
נעביר אגפים ונקבל: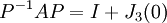
קיבלנו שצורת ז'ורדן הדומה ל-A היא 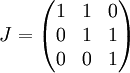
כנדרש! :)