פתרון לינארית 2, אונ' בר אילן, תשנ"ט, מועד א, שאלה 5

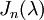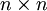
סימון - $J_n(\lambda)$ בלוק ז'ורדן המתאים לע"ע $\lambda$ מסדר $n\times n$

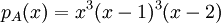
$p_A(x)=x^{3}(x-1)^{3}(x-2)$

הפ"מ מחלק את הפ"א, ולכן ישנן 9 אפשרויות עבור הפ"מ (באופן כללי - מס' הפ"מ האפשריים בהינתן פ"א הוא כפל כל המעריכים שבפ"א - קומבינטוריקה פשוטה). מדובר בבדיקה מייגעת ולא מתוחכמת, אבל כנראה שאין ברירה -- נבדוק את כל האפשרויות.

נזכור ראשית שהחזקה של הגורם 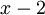$\ x-2$ בפולינום המינימלי של A = גודל הבלוק הגדול ביותר המתאים לע"ע 2 בצורת ז'ורדן של המטריצה = 1; לכן מופיע בלוק ז'ורדן של 2 מסדר 1. אבל הריבוי האלגברי של הע"ע 2 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 2 בצורת ז'ורדן=1, ולכן בכל צורות ז'ורדן האפשריות יש בדיוק בלוק אחד שמתאים ל-2, והוא מסדר 1.

באופן דומה הריבוי האלגברי של הע"ע 1 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 1 בצורת ז'ורדן=3, ו- הריבוי האלגברי של הע"ע 0 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 0 בצורת ז'ורדן=3.

כעת, עבור כל פ"מ, נמקם ראשית את 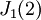$J_1(2)$ בצורת הז'ורדן, ואז נוכל להתעלם מהע"ע 2, שכן 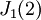$J_1(2)$ חייב להיות המופע היחיד של הע"ע 2 בצורת ז'ורדן (כי סכום גדלי הבלוקים המתאימים לע"ע 2 צריך להיות 1=המעריך המתאים בפ"א, כפי שכבר פירטתי), ונשים בכל פעם את הבלוקים שחייבים להופיע לפי החזקה המתאימה בפ"מ, ונראה כמה חופש בחירה נותר לנו.

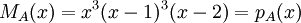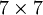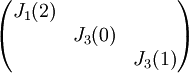1) עבור פ"מ $M_A(x)=x^{3}(x-1)^{3}(x-2)=p_A(x)$ , צורת ז'ורדן נקבעת באופן יחיד. הרי אנו יודעים שבצורת ז'ורדן חייב להופיע בלוק המתאים לע"ע i, מסדר השווה לחזקה שלו בפ"מ - ונקבל שהמטר' שקיבלנו ע"י הכנסת הבלוקים שחייבים להופיע היא כבר מסדר $7\times7$ , ולכן היא צורת ז'ורדן. צורת ז'ורדן היא $\begin{pmatrix} J_1(2)& & \\ & J_3(0) & \\ & & J_3(1) \end{pmatrix}$ .

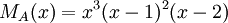2) עבור פ"מ $M_A(x)=x^{3}(x-1)^{2}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

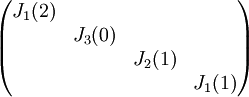
צורת ז'ורדן היא $\begin{pmatrix} J_1(2) & & & \\ & J_3(0) & & \\ & & J_2(1) & \\ & & & J_1(1) \end{pmatrix}$

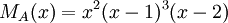3) עבור פ"מ $M_A(x)=x^{2}(x-1)^{3}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

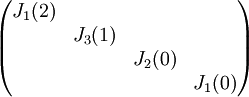
צורת ז'ורדן היא $\begin{pmatrix} J_1(2) & & & \\ & J_3(1) & & \\ & & J_2(0) & \\ & & & J_1(0) \end{pmatrix}$

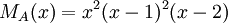4) עבור פ"מ $M_A(x)=x^{2}(x-1)^{2}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

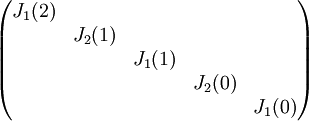
צורת ז'ורדן היא $\begin{pmatrix} J_1(2)& & & & \\ & J_2(1)& & & \\ & & J_1(1) & & \\ & & & J_2(0) & \\ & & & & J_1(0) \end{pmatrix}$

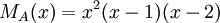5) עבור פ"מ $M_A(x)=x^{2}(x-1)(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

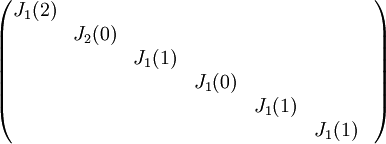
צורת ז'ורדן היא $\begin{pmatrix} J_1(2) & & & & & & \\ & J_2(0) & & & & & \\ & & J_1(1) & & & \\ & & &J_1(0) & & \\ & & & & J_1(1) & \\ & & & & &J_1(1) \\ \end{pmatrix}$

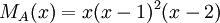6) עבור פ"מ $M_A(x)=x(x-1)^{2}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

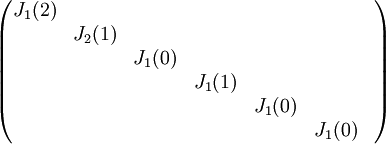
צורת ז'ורדן היא $\begin{pmatrix} J_1(2) & & & & & & \\ & J_2(1) & & & & & \\ & & J_1(0) & & & \\ & & &J_1(1) & & \\ & & & & J_1(0) & \\ & & & & &J_1(0) \\ \end{pmatrix}$

בכך ענינו על סעיף ב'.

7) עבור פ"מ 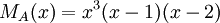$M_A(x)=x^{3}(x-1)(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

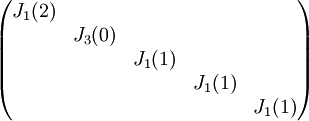
צורת ז'ורדן היא $\begin{pmatrix} J_1(2)& & & & \\ & J_3(0)& & & \\ & & J_1(1) & & \\ & & & J_1(1) & \\ & & & & J_1(1) \end{pmatrix}$

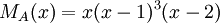8) עבור פ"מ $M_A(x)=x(x-1)^{3}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

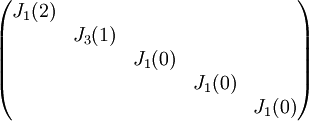
צורת ז'ורדן היא $\begin{pmatrix} J_1(2)& & & & \\ & J_3(1)& & & \\ & & J_1(0) & & \\ & & & J_1(0) & \\ & & & & J_1(0) \end{pmatrix}$

9) לבסוף, עבור הפ"מ 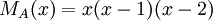$M_A(x)=x(x-1)(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד, שכן כל הבלוקים הם מסדר 1, והרי המספר של הבלוקים המתאימים לכל ע"ע נקבע חד-משמעית ע"י הפ"א.

צורת ז'ורדן היא

כלומר, לכל אחת מ-9 האפשרויות יש בדיוק צורת ז'ורדן אפשרית אחת. לכן יש 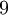$9$ צורות ז'ורדן אפשריות בסה"כ!

מש"ל.

למרצים: השאלה במבחן הדוגמא המתאים לאותה השנה זהה לחלוטין עד כדי מספרים שונים. האם צריך לפתור גם אותה?

הערות: 1) בפתרון הנחתי שצורת ז'ורדן שמתקבלת מסדר שונה של הבלוקים באלכסון היא זהה. (זה בסדר כי הן דומות; אם רוצים דווקא להחשיב אותן בנפרד, צריך להכפיל את האפשרויות שבכל מקרה ב(עצרת של (מס' הבלוקים שבצורת ז'ורדן))) לכן בכל מקום שבו כתוב 'יחיד/ה' על צורת ז'ורדן, הכוונה היא עד כדי שינוי סדר הבלוקים.

2)כאשר במטריצה לא מופיעים במפורש איברים - המקומות החסרים הם אפסים.

פתרון לינארית 2, אונ' בר אילן, תשנ"ט, מועד א, שאלה 5

Math-Wiki