הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' עברית, תשס"ח, מועד ב, שאלה 5"
מתוך Math-Wiki
| (8 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 15: | שורה 15: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | אנו יודעים כי מטריצות | + | אנו יודעים כי מטריצות הן דומות '''אם ורק אם''' יש להן אותה צורת ג'ורדן (עד כדי שינוי סדר הבלוקים). |
| − | + | נחשב את צורת ג'ורדן של כל אחחת מהמטריצות הנ"ל. | |
| + | |||
| + | <math>D</math> היא אלכסונית, ובפרט '''כבר''' בצורת ג'ורדן. לכן, צורת ג'ורדן שלה היא | ||
| + | <math>\begin{pmatrix} | ||
6 &0 \\ | 6 &0 \\ | ||
0 &-2 | 0 &-2 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math>. |
| − | + | <math> | |
| − | x-2 &8 \\ | + | .p_{A}(x)=\begin{vmatrix} |
| − | 2 &x-2 | + | x-2 &-8 \\ |
| − | \end{vmatrix}=(x-2)^{2}-16=x^{2}-4x-12=(x-6)(x+2)</math> | + | -2&x-2 |
| + | \end{vmatrix} | ||
| + | =(x-2)^{2}-16=x^{2}-4x-12=(x-6)(x+2) | ||
| + | </math> | ||
| + | |||
| + | קיבלנו שיש ל <math>A</math> שני ערכים עצמיים שונים | ||
| + | <math>6,-2</math>, ולכן היא לכסינה, ודומה למטריצה | ||
| + | <math>\begin{pmatrix} | ||
6 &0 \\ | 6 &0 \\ | ||
0 &-2 | 0 &-2 | ||
| − | \end{pmatrix}</math> | + | \end{pmatrix}</math>, שהיא בצורת ג'ורדן, ולכן זו צורת ג'ורדן של <math>A</math>. |
| − | נחשב את צורת | + | <math>,p_{C}(x)=\begin{vmatrix} |
| + | x-2 &-4 \\ | ||
| + | -4 &x-2 | ||
| + | \end{vmatrix}=(x-2)^{2}-16=x^{2}-4x-12=(x-6)(x+2)</math> | ||
| + | ולכן כמו במקרה הקודם, צורת ג'ורדן של <math>C</math> | ||
| + | היא | ||
| + | <math>\begin{pmatrix} | ||
| + | 6 &0 \\ | ||
| + | 0 &-2 | ||
| + | \end{pmatrix}</math>. | ||
| + | |||
| + | נחשב את צורת ג'ורדן של <math>B</math>: | ||
| + | |||
| + | <math>p_{B}(x)=\begin{vmatrix} | ||
x-2 &0 \\ | x-2 &0 \\ | ||
| − | 2 &x-2 | + | -2&x-2 |
| − | \end{vmatrix}=(x-2)^{2}-0=(x-2)^{2}</math> כעת צריך לחשב את הפולינום המינימלי של <math>B</math>. קל לראות כי <math> | + | \end{vmatrix}=(x-2)^{2}-0=(x-2)^{2}</math> |
| + | כעת צריך לחשב את הפולינום המינימלי של <math>B</math>. | ||
| + | קל לראות כי <math>m_{B}(x)=(x-2)^{2}</math> (שכן <math>(B-2I)\neq 0</math>) | ||
| + | ולכן צורת ג'ורדן של <math>B</math> היא | ||
| + | <math>\begin{pmatrix} | ||
2 &1 \\ | 2 &1 \\ | ||
0 &2 | 0 &2 | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | + | בסה"כ קבלנו כי<math> A\sim C\sim D</math> ו <math>B</math> אינה דומה לאף מטריצה מבניהם. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
גרסה אחרונה מ־16:48, 28 בדצמבר 2011
אלו מבין המטריצות הבאות דומות?
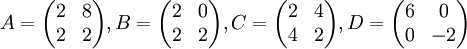
אנו יודעים כי מטריצות הן דומות אם ורק אם יש להן אותה צורת ג'ורדן (עד כדי שינוי סדר הבלוקים).
נחשב את צורת ג'ורדן של כל אחחת מהמטריצות הנ"ל.
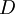 היא אלכסונית, ובפרט כבר בצורת ג'ורדן. לכן, צורת ג'ורדן שלה היא
היא אלכסונית, ובפרט כבר בצורת ג'ורדן. לכן, צורת ג'ורדן שלה היא
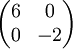 .
.
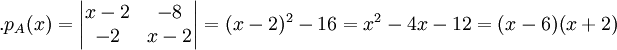
קיבלנו שיש ל  שני ערכים עצמיים שונים
שני ערכים עצמיים שונים
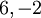 , ולכן היא לכסינה, ודומה למטריצה
, ולכן היא לכסינה, ודומה למטריצה
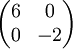 , שהיא בצורת ג'ורדן, ולכן זו צורת ג'ורדן של
, שהיא בצורת ג'ורדן, ולכן זו צורת ג'ורדן של  .
.
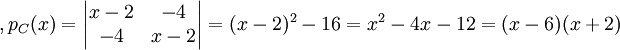 ולכן כמו במקרה הקודם, צורת ג'ורדן של
ולכן כמו במקרה הקודם, צורת ג'ורדן של 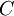 היא
היא
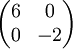 .
.
נחשב את צורת ג'ורדן של  :
:
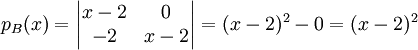 כעת צריך לחשב את הפולינום המינימלי של
כעת צריך לחשב את הפולינום המינימלי של  .
קל לראות כי
.
קל לראות כי 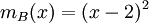 (שכן
(שכן 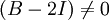 )
ולכן צורת ג'ורדן של
)
ולכן צורת ג'ורדן של  היא
היא
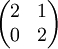
בסה"כ קבלנו כי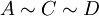 ו
ו  אינה דומה לאף מטריצה מבניהם.
אינה דומה לאף מטריצה מבניהם.