פתרון לינארית 2, אונ' עברית, תשס"ט, מועד א, שאלה 10

כל שתי מטריצות 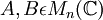$A,B\epsilon M_{n}(\mathbb{C})$ שמקיימות

$f_{A}(t)=f_{B}(t)=(t-1)^{3}(t-2)^{2}(t-3), m_{A}(t)=m_{B}(t)=(t-1)^{2}(t-2)(t-3)$

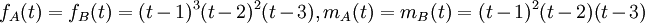
הן דומות.

נוכיח כי לשתיהן אותה צורת ג'ורדן, ונקבל כי הנן דומות עקב כך.

קודם כל, מפני שהמטריצות הנן מעל 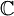$\mathbb{C}$, הן מתפרקות לגומרים לינאריים, ולכן סכום הריבויים האלגבריים הינו סדר המטריצה. לכן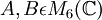 $A,B\epsilon M_{6}(\mathbb{C})$

מפני שנשתמש בפולינום האופייני ובפולינום המינימלי בלבד, הדברים שנגיד פה יהיו נוכנים לגבי A,B כאחד. אני אשתמש בA בשביל הנוחות בלבד.

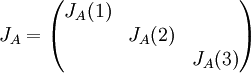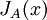נחשב את מטריצת הגו'רדן של A. $J_{A}=\begin{pmatrix} J_{A}(1) & & \\ & J_{A}(2) & \\ & & J_{A}(3) \end{pmatrix}$ כאשר $J_{A}(x)$ הינו הבלוק בצורת הג'ורדן של A הכולל את כל הבלוקים של הערך העצמי x.

קל לראות כי הבלוק של 3 הוא מגודל 1 ולכן הוא פשוט המטריצה 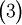$\begin{pmatrix} 3 \end{pmatrix}$. לגבי הע"ע 2, הגודל של הבלוק של כל המטריצות של 2, אך הבלוק הגדול ביותר של 2 הוא מגודל 1. לכן זה 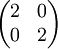$\begin{pmatrix} 2 &0 \\ 0 & 2 \end{pmatrix}$ ולגבי 1, הבלוק של כל המטרצות של הערך 1 הוא מגדול 3. אך הבלוק הגדול ביותר של 1 הינו מגודל 2. לכן זה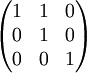 $\begin{pmatrix} 1 &1 &0 \\ 0 & 1 &0 \\ 0 &0 &1 \end{pmatrix}$

ובסה"כ נקבל כי 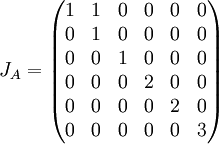$J_{A}=\begin{pmatrix} 1 &1 & 0 &0 & 0 &0 \\ 0 &1 & 0 &0 &0 &0 \\ 0 &0 &1 &0 &0 &0 \\ 0 &0 &0 &2 &0 &0 \\ 0 &0 &0 &0 & 2 &0 \\ 0 & 0 &0 &0 & 0 &3 \end{pmatrix}$ ומיכון שכל מה שעשינו תקף גם לגבי B, נקבל כי גם 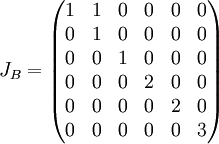$J_{B}=\begin{pmatrix} 1 &1 & 0 &0 & 0 &0 \\ 0 &1 & 0 &0 &0 &0 \\ 0 &0 &1 &0 &0 &0 \\ 0 &0 &0 &2 &0 &0 \\ 0 &0 &0 &0 & 2 &0 \\ 0 & 0 &0 &0 & 0 &3 \end{pmatrix}$ ובה"כ $J_{A}=J_{B}$

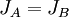
וקבלנו כי 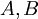$A,B$ דומות.

שאלה: האם יש יש משפט שאומר שאם הפול' האופייני והמינימלי שווים, אז למטריצות ישנן אותה צורת ג'ורדן?

תשובה: לא. למשל המטריצות הבאות אינן דומות, כי שתיהן בצורת ג'ורדן והיא לא זהה (גם לא עד כדי סדר הבלוקים), אבל לשתיהן פולינום אופייני 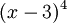$(x-3)^4$ ופולינום מינימלי 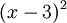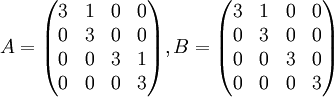$(x-3)^2$: $A=\begin{pmatrix} 3 & 1 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 3 & 1\\ 0 & 0 & 0 & 3\\ \end{pmatrix} , B=\begin{pmatrix} 3 & 1 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 3\\ \end{pmatrix}$ ב.צ.