שיחה:88-113 סמסטר א' תשעא/קבוצת דיון-עדי ניב
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
פעולות שורה ועמודהֿ
רק כדי להיות בטוח- דט' של מט' שהפעלנו עליה פעולות שורה וגם עמודה, שווה לדט' של המטריצה המקורית, נכון?
- (לא מתרגל/ת): לא:
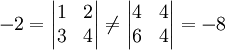 למרות שהכפלנו את השורה הראשונה והעמודה הראשונה ב-2. עם זאת, הדט' של מט' שהפעלנו עליה החלפת שורות וגם עמודות או הוספת מכפלת שורה/עמודה בסקלר - שווה לדט' של המטריצה המקורית (כי הוספת מכפלת שורה/עמודה בסקלר לא משנה את הדטרמיננטה והחלפת שורות k פעמים ב-A ו-k פעמים ב-
למרות שהכפלנו את השורה הראשונה והעמודה הראשונה ב-2. עם זאת, הדט' של מט' שהפעלנו עליה החלפת שורות וגם עמודות או הוספת מכפלת שורה/עמודה בסקלר - שווה לדט' של המטריצה המקורית (כי הוספת מכפלת שורה/עמודה בסקלר לא משנה את הדטרמיננטה והחלפת שורות k פעמים ב-A ו-k פעמים ב-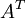 מכפילה את הדט' ב-
מכפילה את הדט' ב-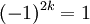 ). אור שחףשיחה 11:39, 8 בנובמבר 2010 (IST)
). אור שחףשיחה 11:39, 8 בנובמבר 2010 (IST)
- גם לא מתרגלת: אבל למדנו שאחרי כפל שורה במטריצה פי a צריך לחלק את הדטרמיננטה ב-a. אז בהנחה שכך זה גם לגבי עמודה, אם כפלת פעמיים פי 2, צריך לחלק ב-4 ואז יצא שיוויון. כך שזו לא דוגמה נגדית כלל. אז אני מצטרפת לשאלה!
- כל שני מספרים שווים עד כדי כפל בקבוע, זה לא אומר שהם שווים באמת. --ארז שיינר 21:46, 8 בנובמבר 2010 (IST)
- (לא מתרגל/ת): תשובה נוספת: כמובן שדט' של מט' שהפעלנו עליה פעולות שורה וגם עמודה ושחילקנו אותה (את הדטרמיננטה) בכל הסקלרים שבהם הכפלנו את השורות והעמודות, שווה לדט' של המטריצה המקורית, אבל זו לא הייתה השאלה. אור שחףשיחה 22:12, 8 בנובמבר 2010 (IST)
- גם לא מתרגלת: אבל למדנו שאחרי כפל שורה במטריצה פי a צריך לחלק את הדטרמיננטה ב-a. אז בהנחה שכך זה גם לגבי עמודה, אם כפלת פעמיים פי 2, צריך לחלק ב-4 ואז יצא שיוויון. כך שזו לא דוגמה נגדית כלל. אז אני מצטרפת לשאלה!
מרחב וקטורי נוצר סופית
מותר לנו להניח שכל המ"ו בתרגילים הם ממימד סופי, גם אם זה לא מצויין מפורשות? אור שחףשיחה 20:05, 8 בנובמבר 2010 (IST)
תרגיל 4 שאלה 2
בתרגיל כתוב למצוא את 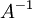 על ידי שימוש בפרוק
על ידי שימוש בפרוק 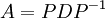 . לא הבנתי מה הכוונה, הדבר היחיד הקשור שמצאתי זה ש-
. לא הבנתי מה הכוונה, הדבר היחיד הקשור שמצאתי זה ש- 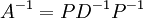 אבל אם כבר מחשבים את
אבל אם כבר מחשבים את  אז פשוט יותר לחשב את
אז פשוט יותר לחשב את  בדרך ה"רגילה" (דירוג (A|I)) וזהו, לא?
בדרך ה"רגילה" (דירוג (A|I)) וזהו, לא?
בעצם מהי הדרך הפשוטה והקצרה ביותר לחשב את 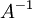 ?
?
- עבור
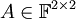 הדרך הפשוטה ביותר היא
הדרך הפשוטה ביותר היא 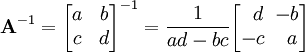
- ועבור
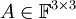 :
: 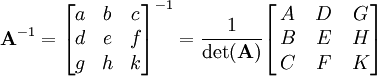
- כאשר
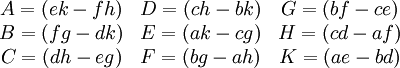
- (מתוך ויקי האנגלית). באופן כללי עדיף לחשב לפי דירוג או adj (מתוך השיטות שכבר למדנו. בוויקיפדיה העברית כתוב שיש שיטות הרבה יותר יעילות, אבל לא נוח ליישם אותן). עם זאת, זה לא רלוונטי כי בתרגיל ביקשו דווקא לפי PDP-1.
- תודה על התשובה. זה בעצם
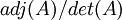 ולמדנו את זה. אני לא רואה היגיון בלחשב את
ולמדנו את זה. אני לא רואה היגיון בלחשב את 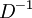 באמצעות שיטה לבחירתי, ואז לחשב את
באמצעות שיטה לבחירתי, ואז לחשב את 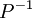 , ואז לכפול שלוש מטריצות, וכל זה במקום חישוב יחיד של
, ואז לכפול שלוש מטריצות, וכל זה במקום חישוב יחיד של 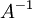 בדרך לבחירתי. למה זה?? אגב, בטוח שהדירוג של (A|I) לא קצר יותר מחישוב
בדרך לבחירתי. למה זה?? אגב, בטוח שהדירוג של (A|I) לא קצר יותר מחישוב 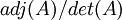 ?
?
- תודה על התשובה. זה בעצם
- מה מיוחד במטריצה D? להפוך אותה לוקח שנייה וחצי ולא צריך שום אלגוריתם. --ארז שיינר 23:45, 8 בנובמבר 2010 (IST)
- אה התבלבלתי בסימון, התכוונתי להפוך את P באמצעות שיטה לבחירתי, ואז להפוך את D, ואז לכפול שלוש מטריצות. החישוב של ההפוכה ל-P הוא מסובך כמו החישוב של ההפוכה של A, לא? אז איפה ההיגיון...
- כי עם P-1 אפשר לחשב גם את A3. אמנם 3 זה לא הרבה, אבל מה אם היו שואלים אותנו על A20? או על A10000? אפילו wolframalpha ויתר. ובלי שום קשר - תשובה?. אור שחףשיחה 00:00, 9 בנובמבר 2010 (IST)
- אופס, בעצם הוא לא ויתר. פשוט אין לו כוח להציג את <צונזר על מנת לשמור על שפיות הדף> אבל ב-100000000 הוא נכנע.
- כי עם P-1 אפשר לחשב גם את A3. אמנם 3 זה לא הרבה, אבל מה אם היו שואלים אותנו על A20? או על A10000? אפילו wolframalpha ויתר. ובלי שום קשר - תשובה?. אור שחףשיחה 00:00, 9 בנובמבר 2010 (IST)
- אה התבלבלתי בסימון, התכוונתי להפוך את P באמצעות שיטה לבחירתי, ואז להפוך את D, ואז לכפול שלוש מטריצות. החישוב של ההפוכה ל-P הוא מסובך כמו החישוב של ההפוכה של A, לא? אז איפה ההיגיון...
- חח טוב השתכנעתי, תודה.
שאלה
מותר להכניס ו"ע V לתוך דט'? כלומר יש לי דט' של ביטוי כלשהו שווה משהו, מותר להגיד שהדט' של הביטוי כפול V שווה ל V כפול המשהו? תודה