הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏תשובה)
(←‏תשובה)
שורה 39: שורה 39:
  
 
הדרך הנכונה לכפול טורים, בדומה למכפלת סכום, צריכה להוסיף מחוברים רבים אחרים. <math>(a_1+a_2)(b_1+b_2)=a_1b_1+a_2b_2+{\color{red}a_1b_2+a_2b_1}</math>. יש משפטים בנוגע למכפלת טורים, אני לא יודע אם אתם לומדים אותם. --[[משתמש:ארז שיינר|ארז שיינר]] 01:27, 25 בנובמבר 2010 (IST)
 
הדרך הנכונה לכפול טורים, בדומה למכפלת סכום, צריכה להוסיף מחוברים רבים אחרים. <math>(a_1+a_2)(b_1+b_2)=a_1b_1+a_2b_2+{\color{red}a_1b_2+a_2b_1}</math>. יש משפטים בנוגע למכפלת טורים, אני לא יודע אם אתם לומדים אותם. --[[משתמש:ארז שיינר|ארז שיינר]] 01:27, 25 בנובמבר 2010 (IST)
 +
:לא למדנו עוד את לייבניץ אבל הבנתי את התשובה, תודה רבה!
  
 
== משהו לא מובן לגבי טורים... ==
 
== משהו לא מובן לגבי טורים... ==

גרסה מ־13:05, 25 בנובמבר 2010

חזרה לדף הקורס


גלול לתחתית העמוד


הוספת שאלה חדשה

הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).

-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן

אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.

ארכיון

שאלות

בקשר לשאלה 4 בתרגיל 6

בשאלה אנו דרושים למצוא סכומים של סדרות. האם אנו צריכים להוכיח קודם כי קיים גבול ורק אחר כך למצוא אותו, או אפשר ישר למצוא אותו? תודה.

תשובה

חובה גם להוכיח שזה מתכנס. אבל אני לא רואה איך אפשר למצוא את הסכום בלי להוכיח שזה מתכנס ממילא... --ארז שיינר 02:44, 25 בנובמבר 2010 (IST)

תרגיל 7

כאשר אני בודקת התכנסות בהחלט האם אפשר להשתמש בכל המבחני השוואה לטורים חיוביים?

תשובה

אם מדובר בטור חיובי, מותר להשתמש במבחני ההשואה לטורים חיוביים, אם לא אז לא. נא לחדד את השאלה. --ארז שיינר 18:31, 23 בנובמבר 2010 (IST)

התכנסות טורים

בניגוד לבסדרות, שבהן למדנו שסכום ומכפלת סדרות מתנכסות מתכנסים, בטורים למדנו רק על סכום. זה אומר שמכפלת סדרות מתכנסות לא בהכרח מתכנסת? תודה!

תשובה

אני מניח שאתה שואל לגבי מכפלת טורים. מכפלת סדרות הוא כפל איבר איבר, כלומר 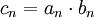c_n=a_n\cdot b_n. אם תגדיר באופן דומה מכפלת טורים, ה"מכפלה" לא בהכרח תתכנס, ואם כן, בוודאי לא למכפלת הסכומים. דוגמאות:


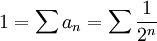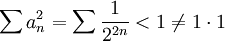
  • 1=\sum a_n=\sum\frac{1}{2^n}, אבל \sum a_n^2 = \sum \frac{1}{2^{2n}} <1 \neq 1\cdot 1
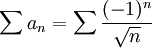  • \sum a_n=\sum\frac{(-1)^n}{\sqrt{n}} מתכנס לפי לייבניץ, אבל אם תכפול אותו בעצמו תקבל את הטור ההרמוני שאינו מתכנס.

הדרך הנכונה לכפול טורים, בדומה למכפלת סכום, צריכה להוסיף מחוברים רבים אחרים. 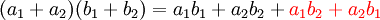(a_1+a_2)(b_1+b_2)=a_1b_1+a_2b_2+{\color{red}a_1b_2+a_2b_1}. יש משפטים בנוגע למכפלת טורים, אני לא יודע אם אתם לומדים אותם. --ארז שיינר 01:27, 25 בנובמבר 2010 (IST)

לא למדנו עוד את לייבניץ אבל הבנתי את התשובה, תודה רבה!

משהו לא מובן לגבי טורים...

בקשר לטורים וסדרת הסכומים החלקיים שלהם- אם הסדרה של הס"חים מתכנסת אז הטור בהכרח מתכנס? או שהסדרה של הס"חים חייבת להתכנס לאפס? כי יש משפט שאומר שאם הטור מתכנס, אז הסדרה של הס"חים מתכנסת לאפס, אני צודק? אז זה אומר שאם יודעים שסדרה של ס"חים מתכנסת אז היא בוודאי מתכנסת? ואם אני יודע שסדרה של ס"חים מתכנסת אבל לא לאפס, זה אומר שהטור מתבדר? תודה

תשובה

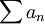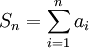תבדיל בין סדרת הסכומים החלקיים, לסדרה של הטור. כלומר, \sum a_n הינו טור, הוא סכום איברי הסדרה a_n. סדרת הסכומים החלקיים הינה S_n=\sum_{i=1}^na_i.

לפי הגדרה טור מתכנס אם סדרת הסכומים החלקיים שלו 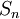S_n מתכנסת, וסכום הטור מוגדר להיות גבול סדרת הסכומים החלקיים. אין הגדרה אחרת להתכנסות טור. סדרת הסכומים החלקיים יכולה להתכנס לכל גבול, ואין לה קשר מיוחד לאפס.

לפי משפט, אם טור מתכנס, הסדרה שלו שואפת לאפס, כלומר 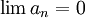\lim a_n = 0. אבל, אם הסדרה הזו שואפת לאפס, אין זה אומר בהכרח שהטור מתכנס (לדוגמא - הטור ההרמוני 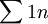\sum{1}{n}). --ארז שיינר 01:31, 25 בנובמבר 2010 (IST)

בדיוק מה שהייתי צריך, תודה רבה.
מקור: https://math-wiki.com/index.php?title=שיחה:88-132_סמסטר_א%27_תשעא&oldid=7919