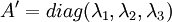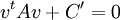שיחה:88-230 סמסטר א' תשעא
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
שאלות
שאלה
איפה התרגיל?
תשובה
אין לתיכוניסטים תרגיל השבוע באינפי 3. (שימו לב, למעלה יש קישור המקל להוסיף שאלות חדשות).
שאלה בנוגע לשניוניות
בקורס שימושי מחשב, המרצה אמר שכל שניונית מהצורה:
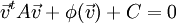
(כאשר 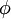 פונקציונל לינארי)
פונקציונל לינארי)
ניתן להמיר לצורה הקנונית שלה, ע"י הזזה באיזשהו וקטור: 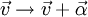
כאשר הוקטור הזה תלוי איכשהו ב-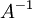 . לאחר ההזזה, מתבטל החלק הלינארי,
. לאחר ההזזה, מתבטל החלק הלינארי, 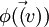 , וניתן רק
למצוא ערכים עצמיים,
, וניתן רק
למצוא ערכים עצמיים, 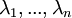 ולקבל שהצורה הקנונית של השניונית היא משהו כמו:
ולקבל שהצורה הקנונית של השניונית היא משהו כמו:
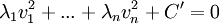 , כאשר
, כאשר 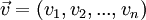
והוא אמר (נראה לי) שאם המטריצה 
לא הפיכה, אזי ניתן להראות שהשניונית אינה ריבועית (או משהו כזה).. השאלה שלי היא, האם באמת ניתן לפעול
בדרך כזו - היא הרבה יותר קצרה..?
תשובה
אני לא רואה איך הזזה בלבד תתקן את החלק הריבועי אם המטריצה A אינה אלכסונית. --ארז שיינר 11:12, 15 באוקטובר 2010 (IST)
- המטרה של ההזזה אינה "לתקן" את החלק הריבועי, אלא את החלק הלינארי.
- דהיינו, כל המטרה בהזזה
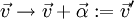 הינה להיפתר
הינה להיפתר - מהחלק הלינארי, לאמור
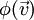 .
.
- דהיינו, כל המטרה בהזזה
- לאחר שנפתרים מהחלק הלינארי, ונשארים עם דבר מהצורה:
- אז, ניתן די בקלות לומר שבמקום המטריצה
 ניתן לשים (או, במילים אחרות, "חילוף קורדינאנטות")
ניתן לשים (או, במילים אחרות, "חילוף קורדינאנטות") - את המטריצה האלכסונית עם הערכים העצמיים: (ב-
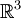 , למשל)
, למשל)
- אז, ניתן די בקלות לומר שבמקום המטריצה
- בדרך זו (אם באמת ניתן לבצע את "הזזת הקסם" הזו) ניתן להסיק את הצורה הקנונית של השניונית די מהר..
אז - האם זה באמת עובד...?
- אז אתם עושים את ההזזה לפני לכסון המטריצה. בכל מקרה לא יודעים את צורת השניונית לפני שמחשבים ע"ע כך שאני לא רואה איך זה יותר פשוט או מהיר. אבל אם זה עובד, זה סבבה מבחינתנו. --ארז שיינר 00:04, 17 באוקטובר 2010 (IST)
- כתוב לי במחברת שצריך לבצע הזזה לפי:
-
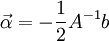
- כאשר,
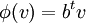 .
.
- כאשר,
- אם מציבים את זה באמת נפטרים מהחלק הלינארי, ומקבלים צורה כמו:
- כאשר,
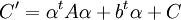 .
.
- כאשר,
- עכשיו באמת ניתן למצוא ערכים עצמיים, ולהחליף את A במטריצה האלכסונים עם הע"ע שלה.
- השאלה - מה קורה כאשר המטריצה
 לא הפיכה?
לא הפיכה?
- השאלה - מה קורה כאשר המטריצה
- במקרה זה אי אפשר להפטר מהחלק הלינארי, כמו למשל בפרבולה. --ארז שיינר 23:36, 17 באוקטובר 2010 (IST)
שאלה בנוגע לתרגילי הבית
האם לקבוצת תרגול של ארז ושל איראנה יהיו תרגילי בית שונים?
- לא, אותו תרגיל. --ארז שיינר 23:34, 17 באוקטובר 2010 (IST)
והאם זה משנה לאיזה קבוצה מגישים?
תרגיל
למתי התרגיל שיש באתר? ("תרגיל 2")
תשובה
יום ראשון כמובן. --ארז שיינר 02:24, 22 באוקטובר 2010 (IST)
- אבל, ארז, בהרצאה בכלל לא הגענו לדיבור על פונקציות, גבולות או רציפות - את שום קשר בין התרגיל להרצאה..
- אין הכרח כזה גם, הידע שרכשתם בתרגיל מספיק בשביל לפתור את התרגיל. --ארז שיינר 13:41, 22 באוקטובר 2010 (IST)
שאלה כללית בקשר לגבולות
האם יש הבדל בין גבול לפי נקודה ששואפת ((x,y)->(0,0)) לבין כל משתנה בנפרד (x->0, y->0)?
תשובה
מה הכוונה כל משתנה בנפרד? הרי למדו שאם קובעים למשל x=0 וy שואף לאפס הגבול יכול להיות שונה מאשר אם נקבע y=0 וניקח את x לשאוף לאפס (קראנו לזה מסלולים, וראינו דוגמאות). --ארז שיינר 18:41, 22 באוקטובר 2010 (IST)
- הכוונה כל משתנה בנפרד היא כמו בשאלה 2 ב' של התרגיל. הכוונה בנקודה ששואפת היא כמו בשאלה 2 סעיף א' של התרגיל. --זיתוני 11:46, 23 באוקטובר 2010 (IST)
- אה, לא. אלה סתם צורות סימון שונות. --ארז שיינר 13:57, 23 באוקטובר 2010 (IST)
שאלה
בקשר להגדרת הגבול של פונקציות. בהרצאה הראינו באופן גיאומטרי עבור כדורים, וכדי להמחיש, נאמר לנו שF של התחום חיתוך הכדור המתאים (ללא המרכז) מוכל ממש בכדור(L,epsilon). רציתי לדעת למה זה מוכל ממש?.. לא יכול להיות מצב בו הם שווים ממש?
- רשמת בעצמך "עבור הכדור המתאים", כלומר יש כדור עבורו זה מוכל ממש. יכול להיות שיש כדור עבורו הם שווים, אז לוקחים כדור קטן יתר והוא המתאים. זה בדיוק כמו ההבדל בגבול סדרות בין
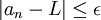 לבין
לבין 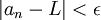 . הגדרת הגבול נשארת זהה אם מחליפים את הקטן ממש בקטן שווה, וכך גם פה. (אם הבנתי נכון את השאלה). --ארז שיינר 16:37, 23 באוקטובר 2010 (IST)
. הגדרת הגבול נשארת זהה אם מחליפים את הקטן ממש בקטן שווה, וכך גם פה. (אם הבנתי נכון את השאלה). --ארז שיינר 16:37, 23 באוקטובר 2010 (IST)
שאלה
בכיתה הוכחנו שהגדרות הגבול לפי היינה וקושי שקולות. בכיוון היינה==>קושי, אני לא בטוח שהבנתי לגמרי מה הרעיון של ההוכחה.. הרעיון הוא להניח בשלילה, לקחת דלתות מהצורה אחד חלקי K (כאשר K רץ על 1,2,...) כך שקיימת סדרה Xk שמתאימה להן שכל רכיב שלה לא מקיים את הגדרת הגבול לפי קושי (זו ההנחה בשלילה), ואז בעצם לקחת את כל הסדרה {Xk} - ומכיוון ששיש לה גבול והוא P (למה זה נכון בכלל?), אבל מצד שני הראינו שאין גבול לפונק', זו סתירה?.. זה קצת מסורבל אצלי, אני ממש לא בטוח שהבנתי נכון.
תשובה
זה דומה לאינפי 1. אם אין התכנסות לפי קושי, זה אומר שיש אפסילון, עבורו בכל כדור קטן כפי שנרצה סביב נקודת הגבול, יש נקודה בה הפונקציה רחוקה מרחק אפסילון ומעלה מהגבול הרצוי. אם נבחר את הנקודה הזו מתוך כל כדור (בסדרת כדורים עם רדיוסים קטנים - אלה הדלתות) נקבל סדרה מתכנסת, אבל הפונקציה על הסדרה לא יכולה להתכנס לגבול הרצוי, בסתירה. --ארז שיינר 01:34, 24 באוקטובר 2010 (IST)
- תודה!
עמוד לקורס מבוא לחישוב
ארז, אתה יכול בבקשה לפתוח עמוד לקורס מבוא לחישוב?
- נפתח.