הבדלים בין גרסאות בדף "שיחה:88-236 תשעא סמסטר קיץ"
(←שאלה 3 סעיף ב') |
(←שאלה בקשר לפתרון תרגיל 1) |
||
| שורה 49: | שורה 49: | ||
בשאלה 9 בתרגיל 1, נתונים 4 קודקודים של טטראדר וצריך לחשב את נפחו. לא הבנתי את דרך הפתרון - חישבנו את נפח המקבילית המתאימה? למה זה דווקא הדטרמיננטה הזו? (למה הצלעות שפורשות את המקבילית הן דווקא הקודקודים של הטטראדר..) אשמח לתשובה. | בשאלה 9 בתרגיל 1, נתונים 4 קודקודים של טטראדר וצריך לחשב את נפחו. לא הבנתי את דרך הפתרון - חישבנו את נפח המקבילית המתאימה? למה זה דווקא הדטרמיננטה הזו? (למה הצלעות שפורשות את המקבילית הן דווקא הקודקודים של הטטראדר..) אשמח לתשובה. | ||
: נפח של טטרהדר <math>V = \frac{1}{3} S\,h \,</math> כאשר S הוא שטח הבסיס. כיוון שנקודה <math>p_1</math> מתלכדת עם הראשית, נבחר, בה"כ: <math>a_1=p_2-p_1,\,a_2=p_3-p_1,\,a_3=q-p_1\,</math>. לכן <math>S = \frac{1}{2} |a_1\times a_2| \,</math>. מכאן ברור כי <math>V = \frac{1}{6} |a_3\cdot a_1\times a_2|= \frac{1}{6} |det(a_1,a_2,a_3)|\,</math>. --[[משתמש:Grisha|Grisha]] 16:18, 31 באוגוסט 2011 (IDT) | : נפח של טטרהדר <math>V = \frac{1}{3} S\,h \,</math> כאשר S הוא שטח הבסיס. כיוון שנקודה <math>p_1</math> מתלכדת עם הראשית, נבחר, בה"כ: <math>a_1=p_2-p_1,\,a_2=p_3-p_1,\,a_3=q-p_1\,</math>. לכן <math>S = \frac{1}{2} |a_1\times a_2| \,</math>. מכאן ברור כי <math>V = \frac{1}{6} |a_3\cdot a_1\times a_2|= \frac{1}{6} |det(a_1,a_2,a_3)|\,</math>. --[[משתמש:Grisha|Grisha]] 16:18, 31 באוגוסט 2011 (IDT) | ||
| + | |||
| + | ==שאלה== | ||
| + | האם מסילות שקולות תמיד קובעות את אותו הקו? | ||
גרסה מ־14:44, 31 באוגוסט 2011
תוכן עניינים
שאלות
ארכיון תרגיל 1
ארכיון תרגיל 2
ארכיון תרגיל 3
תרגיל 4
מתי יעלו פתרונות של תרגיל 2? ו-3? לפחות של 2.....
- מחר --Grisha 19:53, 28 באוגוסט 2011 (IDT)
שאלה
מה לעזאזל? ברצינות
- מצטרף. מה הקשר לקבוצות קומפקטיות פתאום בקורס הזה?
שאלה 3
לא התכוונתם שהדומיין של המשטח יהיה בין 0 ל2pi? אחרת הוא לא מקיף את התחום ויהיה עלינו לחשב כמה אינטגרלים לא סימפטיים (שנראה כי נכתבו בכוונה כדי שייתבטלו בעזרת סטוקס). או שזה יהיה cos(2*Pi*t) וsin(2*Pi*t)?
אכן צריך להיות שם פאי. א' צריך להיות ((γ(s,t)=(2cos(2π t),3sin(2π t)cos(πs),sin(2π t)sin(πt ו-ב' צריך להיות ((γ(t)=(cos(2πt),sin(2πt),sin(2πt [ברק]
שאלה 3 סעיף א'
נתונה פרמטריזציה של פני אליפסואיד, אבל התחום של הפרמטרים הוא בין 0 ל-1, אז מקבלים רק חלק מפני האליפסואיד. האם זאת הייתה הכוונה?
נפלה טעות בניסוח, ראה תשובה לשאלה הבאה. [ברק]
שאלה 3 סעיף ב'
מסילה ב-R^3 היא אינה שפה של אף תחום ב-R^3, ואין לה שפה. כיצד אנו אמורים להשתמש במשפט סטוקס? אודה לכם אם אקבל תשובה מהירה, התרגיל להגשה בעוד כחמישה ימים ויש גם מבחן על הדרך.
מתנצל, צריך להיות בסעיף ב' ((γ(t)=(cos(2πt),sin(2πt),sin(2πt נפלה שגיאה בניסוח השאלה. בסעיף א' אמור להיות:
((γ(s,t)=(2cos(2π t),3sin(2π t)cos(πs),sin(2π t)sin(πs [ברק]
- התשובה אינה פותרת את הבעייתיות של סעיף ב'. למסילה ב-R^3 אין שפה והיא גם לא שפה של תחום כלשהו, אפילו אם היא סגורה.
- אני רק רוצה להוסיף שזה שכתבת "[ברק]" לא מוסיף לך הרבה אמינות. איך אנחנו יודעים שאתה ברק הראל האמיתי או שסתם עובדים עלינו? יש מצב שאתם מתקנים את התרגיל\כותבים מהיוזר המוכר של גרישה כדי למנוע ספק?
שאלה שקשורה להרצאה מספר 2
בהרצאה מספר 2 טענו שהקבוצה M={(x,y) : (x,y) is in [0,1] intersection Q} היא חסרת תכולה. כדי להוכיח זאת, אמרנו שכל קב' מלבנים שאיחודים מכיל את M סכום תכולם הוא לפחות 1. למה זה נכון? (למשל המלבנים המנוונים. הם מכילים את הנק', לא? וסכום תכולתם הוא 0.)
- בסיכום שנמצא באתר יש טעות בהגדרה/משפט (חלק 2) ואי-דיוק קטן.
- קודם כל, מספר תיבות הוא סופי, אנחנו לא מדברים על אוסף אינסופי של תיבות לא חשוב באיזה חלק של משפט.
- ועכשיו תיקון ל-2: אוסף סופי של תיבות שאיחודם מכיל את
(הם בעצמם לא מוכלים ב-) (השאר נכון) - בקשר למספרים רציונליים - קבוצה M מכילה אף תיבה (רק מנוונות), לכן ברור כי
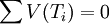. מצד שני, 
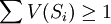(אני מזכיר שמדובר במספר סופי של תיבות ושבין כל שני מספרים רציונאליים שוניים קיים מספר רציונאלי נוסף).--Grisha 16:42, 30 באוגוסט 2011 (IDT)
- תודה רבה (:
שאלה בקשר לפתרון תרגיל 1
בשאלה 9 בתרגיל 1, נתונים 4 קודקודים של טטראדר וצריך לחשב את נפחו. לא הבנתי את דרך הפתרון - חישבנו את נפח המקבילית המתאימה? למה זה דווקא הדטרמיננטה הזו? (למה הצלעות שפורשות את המקבילית הן דווקא הקודקודים של הטטראדר..) אשמח לתשובה.
- נפח של טטרהדר
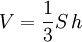כאשר S הוא שטח הבסיס. כיוון שנקודה 
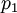מתלכדת עם הראשית, נבחר, בה"כ: 
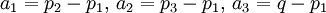. לכן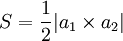 
. מכאן ברור כי 
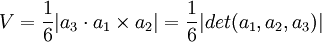. --Grisha 16:18, 31 באוגוסט 2011 (IDT)
שאלה
האם מסילות שקולות תמיד קובעות את אותו הקו?
