שיחת משתמש:Nimrod
מתוך Math-Wiki
תרגיל 1, 4.ג'
צ"ל 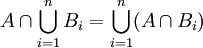 ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש:
ואח"כ אתה משתמש בזה פעמיים (כדי להראות ש: 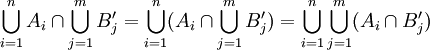 ). -אור שחף, שיחה, 19:01, 26 ביולי 2010 (IDT)
). -אור שחף, שיחה, 19:01, 26 ביולי 2010 (IDT)
תרגיל 1, 2.8א
אתה רוצה להראות ש-![\frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]](/images/math/d/d/7/dd7df529bb078476cb4e7a64580f1e5c.png) . מתקיים:
. מתקיים: 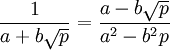 . מכיוון ש-
. מכיוון ש-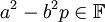 הטענה נכונה. -אור שחף, שיחה, 18:46, 27 ביולי 2010 (IDT)
הטענה נכונה. -אור שחף, שיחה, 18:46, 27 ביולי 2010 (IDT)
![\left(a^2-b^2 p\right)^{-1} \in \mathbb{F} \subset \mathbb{F}[\sqrt{p}]](/images/math/4/0/7/4070ea82ced46be53a16b8802b7c9f08.png) ולכן
ולכן 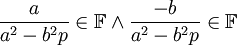 . לפי הגדרת
. לפי הגדרת ![\mathbb{F}[\sqrt{p}]](/images/math/3/5/7/35773cd80c4131ea2053d357c0cc77aa.png) ולפי דיסטריביוטיביות (שאותה צ"ל, זה קל) נובע ש-
ולפי דיסטריביוטיביות (שאותה צ"ל, זה קל) נובע ש-![\frac{a-b\sqrt{p}}{a^2-b^2 p} \in \mathbb{F}[\sqrt{p}]](/images/math/8/0/e/80edb33d38eb027c0169cc471c6432bc.png) ואז, לפי
ואז, לפי 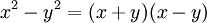 (צ"ל),
(צ"ל), 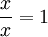 ואסוציאטיביות (צ"ל) מתקיים
ואסוציאטיביות (צ"ל) מתקיים ![\frac{a-b\sqrt{p}}{a^2-b^2 p} = \frac{1}{a+b\sqrt{p}} \in \mathbb{F}[\sqrt{p}]](/images/math/b/d/e/bde6b032f576a7162acca0800a2a1212.png) . -אור שחף, שיחה, 19:44, 27 ביולי 2010 (IDT)
. -אור שחף, שיחה, 19:44, 27 ביולי 2010 (IDT)
בגלל שעדיף לא לציין מה שיש בו טעות אלה רק מה שנכון
![a^2-b^2 p \in \mathbb{F}[\sqrt{p}]](/images/math/e/6/9/e694d6913259da057f288509b94b92b3.png) . ניסיתי להוכיח סגירות:
. ניסיתי להוכיח סגירות: 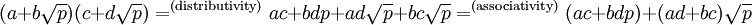 . בזכות הגדרת
. בזכות הגדרת 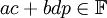 , אבל בגלל קיום איבר נגדי, איבר הופכי וסגירות החיבור והכפל ב-F, צריך להתקיים ש-p שייך ל-F. חכו רגע, או שטעיתי או שיש פה משהו מתוחכם שלא ראיתי. נ.ב. נמרוד, למה מחקת? -
, אבל בגלל קיום איבר נגדי, איבר הופכי וסגירות החיבור והכפל ב-F, צריך להתקיים ש-p שייך ל-F. חכו רגע, או שטעיתי או שיש פה משהו מתוחכם שלא ראיתי. נ.ב. נמרוד, למה מחקת? -