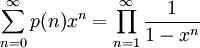הבדלים בין גרסאות בדף "תקציר מבוא לקומבינטוריקה, סמסטר א תשע״ג"
מתוך Math-Wiki
(המשך יבוא) |
(אין הבדלים)
|
גרסה מ־22:17, 2 בפברואר 2013
בתקציר זה, אלא אם צוין אחרת, כל המשתנים והנעלמים שלמים ואי־שליליים למעט 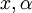 .
. 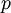 ראשוני ו־
ראשוני ו־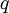 אינו שלם או אי־שלילי רק במקרים בהם הוא מוצג כמשתנה בפולינום.
אינו שלם או אי־שלילי רק במקרים בהם הוא מוצג כמשתנה בפולינום. 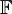 שדה.
שדה.
- נסמן
![[n]:=\{1,2,\dots,n\}=[1,n]\cap\mathbb N](/images/math/f/e/1/fe1f03787412c8bc98ac6a6037b1bc28.png) .
. 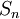 היא קבוצת כל התמורות על
היא קבוצת כל התמורות על ![[n]](/images/math/d/e/5/de504dafb2a07922de5e25813d0aaafd.png) .
. - חלוקת קבוצות של
 ל־
ל־ היא בחירה של תתי־קבוצות
היא בחירה של תתי־קבוצות 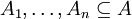 זרות עבורן
זרות עבורן 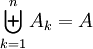 .
. - סדרת פיבונצ׳י תסומן
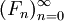 .
. - ריצוף דומינו של
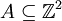 הוא כיסוי של
הוא כיסוי של  על ידי קטעים זרים מאורך 1 שקצותיהם נקודות ב־
על ידי קטעים זרים מאורך 1 שקצותיהם נקודות ב־ .
.
- ללוח בגודל
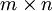 קיים ריצוף דומינו אם״ם
קיים ריצוף דומינו אם״ם 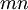 זוגי.
זוגי. - ללוח בגודל
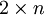 קיימים
קיימים 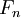 ריצופי דומינו.
ריצופי דומינו.
- ללוח בגודל
- עקרון שובך יונים: בחלוקה של קבוצה סופית
 ל־
ל־ יש לפחות תת־קבוצה אחת שמספר איבריה הוא לכל הפחות
יש לפחות תת־קבוצה אחת שמספר איבריה הוא לכל הפחות 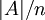 .
. - סימונים:
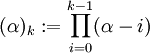 . לכן
. לכן 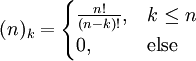 . בנוסף,
. בנוסף, 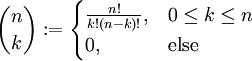 ו־
ו־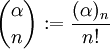 .
. - חליפה: נניח
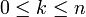 . חליפה של
. חליפה של  איברים מתוך
איברים מתוך  היא
היא  ־יה סדורה של איברים שונים מקבוצה בת
־יה סדורה של איברים שונים מקבוצה בת  איברים (כלומר, חליפה היא בחירה ללא חזרות ועם חשיבות לסדר). מספר החליפות הוא
איברים (כלומר, חליפה היא בחירה ללא חזרות ועם חשיבות לסדר). מספר החליפות הוא 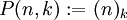 .
.
- תמורה היא חליפה של
 מתוך
מתוך  , ומספר התמורות הוא
, ומספר התמורות הוא 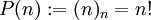 .
. - חליפה עם חזרות היא
 ־יה סדורה של
־יה סדורה של  איברים (לא דווקא שונים) מתוך
איברים (לא דווקא שונים) מתוך  . יש
. יש 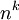 חליפות עם חזרות.
חליפות עם חזרות.
- תמורה היא חליפה של
- צירוף: נניח
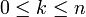 . צירוף של
. צירוף של  איברים מתוך
איברים מתוך  הוא תת־קבוצה של קבוצה בת
הוא תת־קבוצה של קבוצה בת  איברים (כלומר, צירוף הוא בחירה ללא חזרות ובלי חשיבות לסדר). מספר הצירופים הוא
איברים (כלומר, צירוף הוא בחירה ללא חזרות ובלי חשיבות לסדר). מספר הצירופים הוא 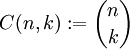 .
.
- צירוף עם חזרות: הוא רב־קבוצה מסדר
 של איברים מתוך קבוצה בת
של איברים מתוך קבוצה בת  איברים. יש
איברים. יש 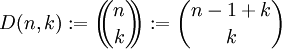 צירופים עם חזרות.
צירופים עם חזרות.
- מספר הצירופים עם חזרות של
 מתוך
מתוך  שווה למספר הדרכים לבחור
שווה למספר הדרכים לבחור  עצמים מתוך
עצמים מתוך  סוגים, ששווה למספר הפתרונות השלמים ואי־שליליים ל־
סוגים, ששווה למספר הפתרונות השלמים ואי־שליליים ל־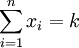 .
.
- מספר הצירופים עם חזרות של
- צירוף עם חזרות: הוא רב־קבוצה מסדר
- הווקטור האופייני של קבוצה
![A\subseteq [n]](/images/math/4/a/1/4a1a50ed9431fb2fda10648006d6259c.png) מוגדר ע״י
מוגדר ע״י 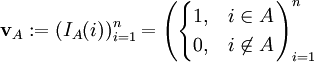 .
. - סדרה אונימוצלית היא סדרה
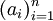 כך שקיים
כך שקיים  עבורו
עבורו 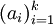 עולה במובן הרחב ו־
עולה במובן הרחב ו־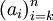 יורדת במובן הרחב.
יורדת במובן הרחב.
-
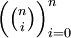 היא סדרה אונימוצלית כאשר אם
היא סדרה אונימוצלית כאשר אם  זוגי אז
זוגי אז 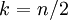 ואחרת
ואחרת 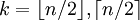 (כי
(כי 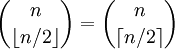 ).
).
-
- הפרת סדר בתמורה
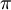 היא זוג
היא זוג 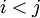 כך ש־
כך ש־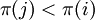 . מספר הפרות הסדר מסומן
. מספר הפרות הסדר מסומן 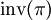 וסימן התמורה מוגדר כ־
וסימן התמורה מוגדר כ־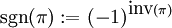 . התמרה
. התמרה 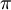 תקרא זוגית אם
תקרא זוגית אם 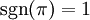 ואי־זוגית אחרת. יש
ואי־זוגית אחרת. יש 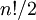 התמרות מכל סוג שסדרן
התמרות מכל סוג שסדרן  .
. - מורד: עבור
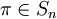 נקרא ל־
נקרא ל־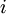 מורָד (descent) אם
מורָד (descent) אם 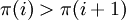 . קבוצת המורדות תסומן
. קבוצת המורדות תסומן 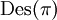 .
.
-
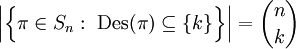 .
.
-
- אם
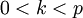 אז
אז 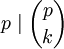 .
. - יהי פולינום
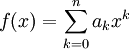 . נסמן
. נסמן 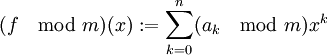 .
. -
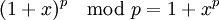 .
. - משפט פרמה הקטן:
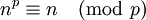 .
. - פיתוח של מספר לפי ראשוני: נניח
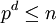 ו־
ו־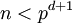 . אזי קיימים
. אזי קיימים 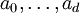 שלמים כך ש־
שלמים כך ש־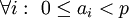 ו־
ו־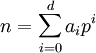 . סכום זה נקרא "הפיתוח של
. סכום זה נקרא "הפיתוח של  לפי
לפי 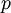 ".
". - אם
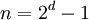 אז
אז 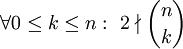 . לפיכך,
. לפיכך, 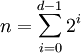 .
. - משפט לוקאס: נניח ש־
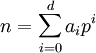 ו־
ו־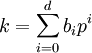 פיתוחים לפי
פיתוחים לפי 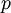 . אזי
. אזי 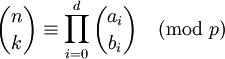 .
. -
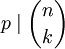 אם״ם בפיתוחים
אם״ם בפיתוחים 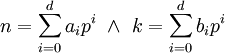 יש
יש 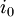 עבורו
עבורו 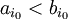 .
. - פירוק/קומפוזיציה של
 הוא הצגה של
הוא הצגה של  כסכום של טבעיים.
כסכום של טבעיים.
- יש
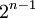 פירוקים של
פירוקים של  (כאשר יש חשיבות לסדר (
(כאשר יש חשיבות לסדר (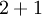 שונה מ־
שונה מ־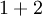 ) וחזרות מותרות (
) וחזרות מותרות (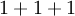 ייספר כפירוק של 3)).
ייספר כפירוק של 3)).
- יש
- מקדם מולטינומי: מספר המילים מאורך
 שבהן המספר
שבהן המספר 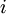 מופיע
מופיע 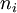 פעמים (
פעמים (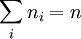 ) הוא
) הוא 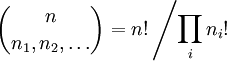 .
. - סימונים:
![[n]_q:=\sum_{i=0}^{q-1}q^i](/images/math/1/1/4/1142fe06d1cef426cc77a95a28921c83.png) . כמו כן,
. כמו כן, ![[n]_q!:=\prod_{i=1}^n [i]_q,\ [0]_q!=1](/images/math/f/0/5/f055a1ad665f2c08934ff04be26853e6.png) ו־
ו־![\forall 0\le k\le n:\ \begin{bmatrix}n\\k\end{bmatrix}_q:=\frac{[n]_q!}{[k]_q![n-k]_q!}](/images/math/7/b/a/7ba8f7b51d561e8c3f8d5412de70b96c.png) . ניתן להראות ש־
. ניתן להראות ש־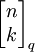 שלם.
שלם.
-
![[n]_1=n](/images/math/2/1/3/2138eba3b871496d1c2aefc842d26ca3.png) ו־
ו־![\forall q\ne 1:\ [n]_q=\frac{q^n-1}{q-1}](/images/math/a/3/f/a3f1a03211830e8a941e8381b013a7b4.png) .
. - אם
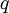 זוגי אז
זוגי אז 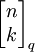 אי־זוגי.
אי־זוגי. - מספר התתי־מרחבים ממימד
 של מרחב וקטורי
של מרחב וקטורי 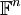 (כאשר ל־
(כאשר ל־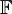 יש
יש 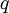 איברים) הוא
איברים) הוא 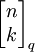 .
.
-
- אם
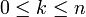 אז
אז ![\begin{bmatrix}n\\k\end{bmatrix}_q\in\mathbb N_0[q]](/images/math/5/e/0/5e038d6e054a2fa4e5d5639801a69b6c.png) , כלומר זה פולינום במשתנה
, כלומר זה פולינום במשתנה 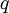 שמקדמיו שלמים ואי־שליליים. למעשה, הוא גם מתוקן, דרגתו
שמקדמיו שלמים ואי־שליליים. למעשה, הוא גם מתוקן, דרגתו 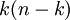 והוא סימטרי (כלומר המקדם של
והוא סימטרי (כלומר המקדם של 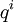 שווה למקדם של
שווה למקדם של 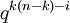 לכל
לכל 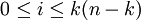 ).
). - הילוך שריג הוא סדרת צעדים בין נקודות ב־
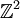 שכל אחד מהם הוא הוספת 1 לאחת מהקואורדינטות של הנקודה בה נמצאים.
שכל אחד מהם הוא הוספת 1 לאחת מהקואורדינטות של הנקודה בה נמצאים.
- יש
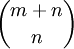 הילוכי שריג מ־
הילוכי שריג מ־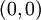 ל־
ל־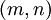 .
. - נסמן
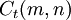 כמספר הילוכי השריג מ־
כמספר הילוכי השריג מ־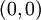 ל־
ל־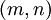 שהשטח המוגבל על־ידם, ציר ה־x והישר
שהשטח המוגבל על־ידם, ציר ה־x והישר 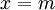 הוא
הוא 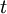 . בנוסף, נגדיר
. בנוסף, נגדיר 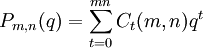 . אזי
. אזי 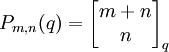 .
.
- יש
- נסמן
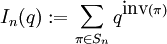 . אזי
. אזי ![I_n(q)=[n]_q!](/images/math/c/7/d/c7d99f5da990a04598408b9fb06ca734.png) .
. - יהי
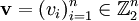 וקטור שרכיביו אפסים ואחדות. אם
וקטור שרכיביו אפסים ואחדות. אם 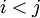 ו־
ו־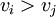 נכנה זאת הפרת סדר. אם נסמן
נכנה זאת הפרת סדר. אם נסמן 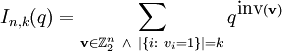 אז
אז 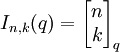 .
. - חלוקה של
 היא וקטור
היא וקטור 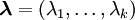 שסכום רכיביו הוא
שסכום רכיביו הוא  (כלומר
(כלומר 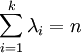 ) והם מסודרים בסדר יורד במובן הרחב. מספר החלוקות מסומן
) והם מסודרים בסדר יורד במובן הרחב. מספר החלוקות מסומן 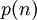 .
.
- מספר החלוקות של
 עם לכל היותר
עם לכל היותר  רכיבים הוא המקדם של
רכיבים הוא המקדם של 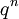 בפולינום
בפולינום 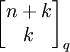 , כלומר
, כלומר 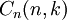 .
.
- מספר החלוקות של
- דיאגרמת יאנג של חלוקה
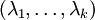 היא דיאגרמת משבצות כך שבשורה ה־
היא דיאגרמת משבצות כך שבשורה ה־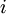 יש
יש 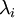 משבצות המיושרות לשמאל.
משבצות המיושרות לשמאל. - הילוכי דיק הם הילוכי שריג מ־
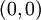 ל־
ל־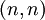 שנמצאים על ומעל הישר
שנמצאים על ומעל הישר  .
. - מספר קטלן הוא מספר הילוכי דיק ל־
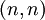 , מסומן
, מסומן 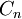 ושווה ל־
ושווה ל־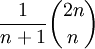 .
.
- נניח ש־
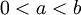 . יש
. יש 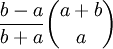 הילוכי דיק ל־
הילוכי דיק ל־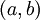 שאינם עוברים על הישר
שאינם עוברים על הישר  למעט בנקודה
למעט בנקודה 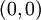 .
. - מילת דיק מאורך
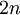 היא סדרה
היא סדרה 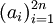 כך ש־
כך ש־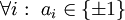 ,
, 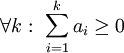 ו־
ו־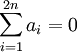 . יש
. יש 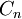 מילות דיק מאורך
מילות דיק מאורך 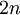 .
. - עץ בינארי שלם/מלא הוא עץ כך שלכל אב יש בדיוק 2 בנים, כלומר לכל קודקוד שאינו עלה יש דרגה 3 למעט קודקוד אחד, שנקרא שורש. אם מבדילים בין הבן הימני לבן השמאלי אז יש
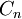 עצים בינארים מלאים עם
עצים בינארים מלאים עם  עלים.
עלים. - בהנתן מכפלה לא קומוטטיבית
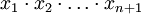 יש
יש 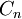 דרכים להוסיף סוגריים למכפלה.
דרכים להוסיף סוגריים למכפלה. - שילוש של מצולע משוכלל בעל
 קודקודים הוא מבנה גיאומטרי הנוצר מהמצולע כשמעבירים בו
קודקודים הוא מבנה גיאומטרי הנוצר מהמצולע כשמעבירים בו 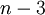 אלכסונים שאינם חותכים זה את זה פרט לבקודקודי המצולע. יש
אלכסונים שאינם חותכים זה את זה פרט לבקודקודי המצולע. יש 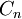 דרכים לשלש מצולע משוכלל בעל
דרכים לשלש מצולע משוכלל בעל 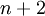 צלעות.
צלעות.
- נניח ש־
- מספר בל הוא מספר חלוקות הקבוצות של
![[n]](/images/math/d/e/5/de504dafb2a07922de5e25813d0aaafd.png) ומסומן
ומסומן 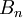 .
. - מספר סטיכלינג מסוג II הוא מספר חלוקות הקבוצות של
![[n]](/images/math/d/e/5/de504dafb2a07922de5e25813d0aaafd.png) ל־
ל־ תתי־קבוצות לא ריקות ומסומן
תתי־קבוצות לא ריקות ומסומן 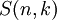 .
.
-
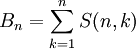 .
. - יהי
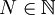 . נסמן
. נסמן 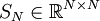 בתור המטריצה שהרכיב בשורה ה־
בתור המטריצה שהרכיב בשורה ה־ ובעמודה ה־
ובעמודה ה־ שלה הוא
שלה הוא 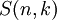 .
. -
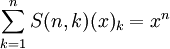 .
.
-
- מספר סטיכלינג הלא מסומן מסוג I הוא מספר התמורות על
![[n]](/images/math/d/e/5/de504dafb2a07922de5e25813d0aaafd.png) עם
עם  מחזורים ומסומן
מחזורים ומסומן 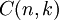 .
.
-
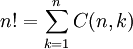 .
. -
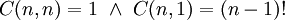 .
.
-
- מספר סטיכלינג מסוג I הוא
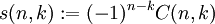 .
.
- יהי
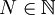 . נסמן
. נסמן 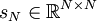 בתור המטריצה שהרכיב בשורה ה־
בתור המטריצה שהרכיב בשורה ה־ ובעמודה ה־
ובעמודה ה־ שלה הוא
שלה הוא 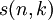 .
. -
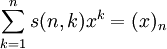 .
.
- יהי
-
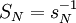 .
.
פונקציות יוצרות
- טור חזקות פורמלי במשתנה
 מכל
מכל 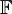 (בד״כ
(בד״כ 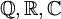 ) הוא ביטוי מהצורה
) הוא ביטוי מהצורה 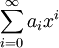 כאשר
כאשר 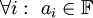 . הטור לא חייב להתכנס. אוסף טורי החזקות הפורמליים ב־
. הטור לא חייב להתכנס. אוסף טורי החזקות הפורמליים ב־ מעל
מעל 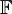 מסומן
מסומן ![\mathbb F[[x]]](/images/math/b/e/5/be54134580c69c9e34ee7950046d7c10.png) .
.
- אם
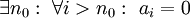 אז הטור הוא פולינום. אוסף הפולינומים ב־
אז הטור הוא פולינום. אוסף הפולינומים ב־ מעל
מעל 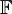 מסומן
מסומן ![\mathbb F[x]](/images/math/a/e/5/ae5d94a2457b0b6d7ccafc8882c1cea4.png) .
.
- אם
- נוסחת טיילור: אם
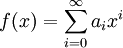 אז
אז 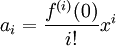 .
. - פונקציה יוצרת: לכל סדרה
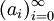 נתאים פונקציה
נתאים פונקציה 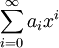 .
. - פונקציה יוצרת מעריכית: לכל סדרה
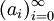 נתאים פונקציה
נתאים פונקציה 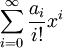 . פונקציות אלה שימושיות לספירת עצמים עבורם הסדר משנה.
. פונקציות אלה שימושיות לספירת עצמים עבורם הסדר משנה. - נרצה לחשב את
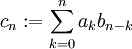 . נגדיר
. נגדיר 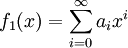 ו־
ו־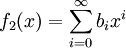 ולכן
ולכן 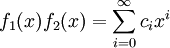 .
. - נרצה למצוא את מספר הפתרונות של
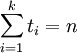 כאשר
כאשר 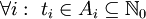 . נתאים לכל משתנה פונקציה יוצרת
. נתאים לכל משתנה פונקציה יוצרת 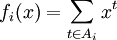 ולכן מספר הפתרונות הדרוש הוא המקדם של
ולכן מספר הפתרונות הדרוש הוא המקדם של 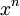 ב־
ב־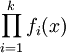 .
. - אם
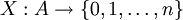 משתנה מקרי כש־
משתנה מקרי כש־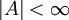 ו־
ו־![f(x)=\sum_{k=0}^n |X^{-1}[\{k\}]|x^k](/images/math/a/f/4/af4c2d3452a815a8b5819ef7757197f5.png) אז
אז 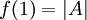 , התוחלת היא
, התוחלת היא 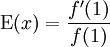 והשונות היא
והשונות היא 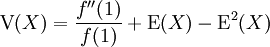 .
.
נוסחאות
- נוסחת הנסיגה של פסקל:
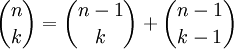
-
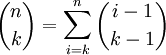
- זהות הקפטן:
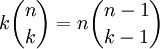
- הבינום של ניוטון:
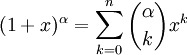
- אם
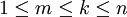 אז
אז 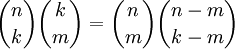
-
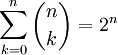
-
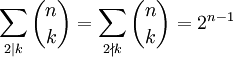
-
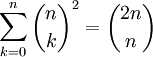
-
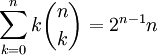
- אם
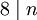 אז
אז 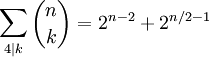
-
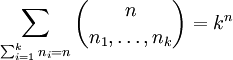
-
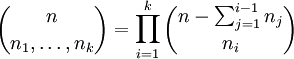
- נוסחת המולטינום:
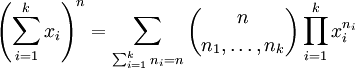
-
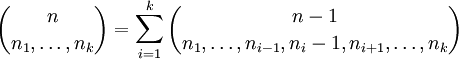
-
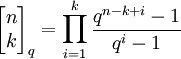
-
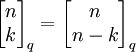
-
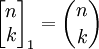
- נוסחת q־פסקל:
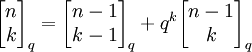
- q־בינום:
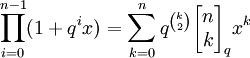
- נוסחת נסיגה למספרי קטלן:
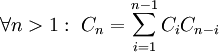 ו־
ו־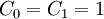
- נוסחת נסיגה למספרי בל:
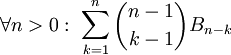 ו־
ו־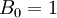
- נוסחת נסיגה למספרי סטיכלינג מסוג II:
![\forall n\in\mathbb N,k\in[n]:\ S(n,k)=S(n-1,k-1)+k S(n-1,k)](/images/math/7/2/e/72eba64aa4e85ec75e17aefa5427f751.png) ו־
ו־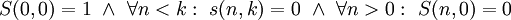
- נוסחת נסיגה למספרי סטיכלינג לא מסומנים מסוג I:
![\forall n\in\mathbb N,k\in[n]:\ C(n,k)=C(n-1,k-1)+(n-1)C(n-1,k)](/images/math/b/a/9/ba92a9c35ebf0407a5eec0f8b687dc35.png) ו־
ו־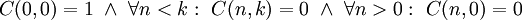
- נוסחת נסיגה למספרי סטיכלינג מסוג I:
![\forall n\in\mathbb N,k\in[n]:\ s(n,k)=s(n-1,k-1)-(n-1)s(n-1,k)](/images/math/4/1/e/41e610c5a909f0516600dbf5f9e833e8.png)
-
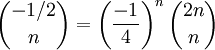
-
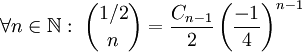
-