הבדלים בין גרסאות בדף "תקציר פיזיקה למתמטיקאים, סמסטר ב תשע״ג"
מתוך Math-Wiki
(יצירת דף עם התוכן "== הקדמה == === יחידות === * '''זמן – שנייה:''' <math>\mathrm s</math> * '''מרחק – מטר:''' <math>\mathrm m</math> * '''מסה – קי...") |
|||
| שורה 1: | שורה 1: | ||
| + | להבא, אלא אם צוין אחרת, נסמן: | ||
| + | * <math>\vec r, \vec v, \vec a</math> פונקציות המיקום, המהירות והתאוצה כפונקציה של הזמן <math>t</math> בהתאמה. | ||
| + | * לכל פונקציה <math>f</math> של הזמן נסמן <math>f_0=f(0)</math> ערך הפונקציה בזמן ההתחלה. | ||
| + | * לכל וקטור <math>\vec u</math> נסמן כ־<math>u=\left|\vec u\right|</math> את גודלו וכ־<math>\hat u=\sgn\!\left(\vec u\right)</math> את כיוונו. | ||
| + | |||
== הקדמה == | == הקדמה == | ||
=== יחידות === | === יחידות === | ||
| שורה 6: | שורה 11: | ||
* '''כוח – ניוטון:''' <math>\mathrm{N=\frac{kg\cdot m}{s^2}}</math> | * '''כוח – ניוטון:''' <math>\mathrm{N=\frac{kg\cdot m}{s^2}}</math> | ||
* '''אנרגיה – ג׳אול:''' <math>\mathrm{J=\frac{kg\cdot m^2}{s^2}=N\cdot m}</math> | * '''אנרגיה – ג׳אול:''' <math>\mathrm{J=\frac{kg\cdot m^2}{s^2}=N\cdot m}</math> | ||
| + | * '''תדירות – הרץ:''' <math>\mathrm{Hz=s^{-1}}</math> | ||
| + | |||
| + | === קבועים === | ||
| + | * '''גודל תאוצת הכובד בקרבת כדה״א:''' <math>g\approx9.8\mathrm\frac ms</math> | ||
=== תזכורות ונוסחאות === | === תזכורות ונוסחאות === | ||
| − | * '''מכפלה וקטורית:''' | + | * '''מכפלה וקטורית:''' <math>\vec u\times\vec v:=\begin{pmatrix}u_yv_z-u_zv_y\\u_zv_x-u_xv_z\\u_xv_y-u_yv_x\end{pmatrix}\simeq\begin{vmatrix}\hat\mathbf x&\hat\mathbf y&\hat\mathbf z\\u_x&u_y&u_z\\v_x&v_y&v_z\end{vmatrix}</math> |
* '''גרדיאנט:''' <math>\nabla f:=\frac{\partial f}{\partial x}\hat\mathbf x+\frac{\partial f}{\partial y}\hat\mathbf y+\frac{\partial f}{\partial z}\hat\mathbf z</math> | * '''גרדיאנט:''' <math>\nabla f:=\frac{\partial f}{\partial x}\hat\mathbf x+\frac{\partial f}{\partial y}\hat\mathbf y+\frac{\partial f}{\partial z}\hat\mathbf z</math> | ||
* '''דיברגנץ:''' <math>\nabla\cdot F:=\frac{\mathrm dF_x}{\mathrm dx}+\frac{\mathrm dF_y}{\mathrm dy}+\frac{\mathrm dF_z}{\mathrm dz}</math> | * '''דיברגנץ:''' <math>\nabla\cdot F:=\frac{\mathrm dF_x}{\mathrm dx}+\frac{\mathrm dF_y}{\mathrm dy}+\frac{\mathrm dF_z}{\mathrm dz}</math> | ||
| שורה 15: | שורה 24: | ||
=== קואורדינטות === | === קואורדינטות === | ||
| − | עבור <math>r,\rho\in[0,\infty)\ \and\ \ | + | עבור <math>x,y,z\in(-\infty,\infty)\ \and\ r,\rho\in[0,\infty)\ \and\ \theta\in(-\pi,\pi]\ \and\ \varphi\in\left[-\frac\pi2,\frac\pi2\right]</math> קואורדינטות כפונקציות של הזמן מתקיים: |
{| border="1" class="wikitable" | {| border="1" class="wikitable" | ||
|- | |- | ||
| שורה 24: | שורה 33: | ||
|- align="left" | |- align="left" | ||
! קרטזיות | ! קרטזיות | ||
| − | | | + | | |
| − | | <math>\begin{array}{l} | + | | <math>\begin{array}{l} \rho=\sqrt{x^2+y^2}\\\theta=\mbox{atan2}(y,x)\\z=z\end{array}</math> |
| − | | <math>\begin{array}{l} | + | | <math>\begin{array}{l} r=\sqrt{x^2+y^2+z^2}\\\theta=\mbox{atan2}(y,x)\\\varphi=\arccos(z/r)\end{array}</math> |
|- align="left" | |- align="left" | ||
! גליליות | ! גליליות | ||
| − | | <math>\begin{array}{l} x= | + | | <math>\begin{array}{l} x=\rho\cos(\theta)\\y=\rho\sin(\theta)\\z=z\end{array}</math> |
| | | | ||
| − | | <math>\begin{array}{l} | + | | <math>\begin{array}{l} r=\sqrt{\rho^2+z^2}\\\theta=\theta\\\varphi=\arctan(\rho/z)\end{array}</math> |
|- align="left" | |- align="left" | ||
! כדוריות | ! כדוריות | ||
| − | | <math>\begin{array}{l} x= | + | | <math>\begin{array}{l} x=r\sin(\varphi)\cos(\theta)\\y=r\sin(\varphi)\sin(\theta)\\z=r\cos(\varphi)\end{array}</math> |
| − | | <math>\begin{array}{l} | + | | <math>\begin{array}{l} \rho=r\sin(\varphi)\\\theta=\theta\\z=r\cos(\varphi)\end{array}</math> |
| | | | ||
|} | |} | ||
כאשר <math>\mbox{Im}(\arctan)=\left[-\frac\pi2,\frac\pi2\right]</math> ו־<math>\mbox{atan2}(y,x):=\begin{cases}\arctan(y/x)&x>0\\\arctan(y/x)+\sgn(y)\pi&x<0\\\sgn(y)\frac\pi2&x=0\ \and y\ne0\\\text{undefined}&x=y=0\end{cases}</math>. | כאשר <math>\mbox{Im}(\arctan)=\left[-\frac\pi2,\frac\pi2\right]</math> ו־<math>\mbox{atan2}(y,x):=\begin{cases}\arctan(y/x)&x>0\\\arctan(y/x)+\sgn(y)\pi&x<0\\\sgn(y)\frac\pi2&x=0\ \and y\ne0\\\text{undefined}&x=y=0\end{cases}</math>. | ||
| − | כמו כן, <math>\mathrm dx\mathrm dy\mathrm dz= | + | כמו כן, <math>\mathrm dx\mathrm dy\mathrm dz=\rho\mathrm d\rho\mathrm d\theta\mathrm dz=r^2\sin(\varphi)\mathrm dr\mathrm d\varphi\mathrm d\theta</math>. |
| + | |||
| + | == קינמטיקה == | ||
| + | * <math>\vec v=\dot\vec r\ \and\ \vec a=\dot\vec v\ \and\ \omega=\dot\theta</math>. | ||
| + | * '''תנועה במהירות קבועה:''' <math>\vec v(t)\equiv\vec v_0</math>. אזי <math>\vec r=\vec v_0t+\vec r_0</math>. | ||
| + | * '''תנועה בתאוצה קבועה:''' <math>\vec a(t)\equiv\vec a_0</math>. אזי <math>\vec v=\vec a_0t+\vec v_0</math> ו־<math>\vec r=\frac\vec a2 t^2+\vec v_0t+\vec r_0</math>. | ||
| + | * '''תנועה בגודל מהירות קבוע:''' <math>|\vec v|\equiv\text{const.}</math>. זה קורה אם״ם <math>\vec a\perp\vec v</math>. | ||
| + | * '''תנועה כללית במעגל:''' אם תנועת הגוף במעגל המונח על המישור <math>xy</math> שרדיוסו <math>R</math> אזי <math>\vec r=R\begin{pmatrix}\cos(\theta)\\\sin(\theta)\\0\end{pmatrix}</math>, <math>\vec v=\omega R\begin{pmatrix}-\sin(\theta)\\\cos(\theta)\\0\end{pmatrix}</math>, ו־<math>\vec a=\vec a_R+\vec a_T</math> כאשר <math>\vec a_R=-\omega^2 R\begin{pmatrix}\cos(\theta)\\\sin(\theta)\\0\end{pmatrix}=-\omega^2\vec r</math> נקראת '''התאוצה הרדיאלית''' והיא אחראית לשינוי בכיוון המהירות ו־<math>\vec a_T=\dot\omega R\begin{pmatrix}-\sin(\theta)\\\cos(\theta)\\0\end{pmatrix}=\frac\dot\omega\omega\vec v</math> נקראת '''התאוצה הטנגנטית/משיקית''' והיא אחראית לשינוי בגודל המהירות. אם נסמן <math>\vec\omega:=\omega\hat\mathbf z</math> נקבל <math>\vec v=\vec\omega\times\vec r</math> ו־<math>\vec a_R=\vec\omega\times\vec v\ \and\ \vec a_T=\dot\vec\omega\times\vec r</math>. | ||
| + | :* '''תנועה קצובה במעגל:''' תנועת גוף במעגל כנ״ל כך ש־<math>\omega(t)\equiv\text{const.}</math>. לכן <math>\theta=\omega t+\theta_0</math> ו־<math>\vec a_T=\vec0\ \and\ a_R=\frac{v^2}R</math>. התאוצה נקראת צנטריפטלית. | ||
| + | ::* '''התדירות''' מוגדרת כ־<math>f:=\frac\omega{2\pi}</math>. | ||
| + | ::* '''זמן המחזור''' מוגדר כ־<math>T:=f^{-1}=\frac{2\pi}\omega</math>. | ||
גרסה מ־16:29, 28 באפריל 2013
להבא, אלא אם צוין אחרת, נסמן:
-
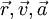 פונקציות המיקום, המהירות והתאוצה כפונקציה של הזמן
פונקציות המיקום, המהירות והתאוצה כפונקציה של הזמן 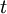 בהתאמה.
בהתאמה. - לכל פונקציה
 של הזמן נסמן
של הזמן נסמן 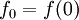 ערך הפונקציה בזמן ההתחלה.
ערך הפונקציה בזמן ההתחלה. - לכל וקטור
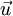 נסמן כ־
נסמן כ־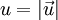 את גודלו וכ־
את גודלו וכ־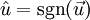 את כיוונו.
את כיוונו.
תוכן עניינים
הקדמה
יחידות
- זמן – שנייה:
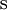
- מרחק – מטר:
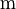
- מסה – קילוגרם:
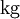
- כוח – ניוטון:
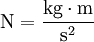
- אנרגיה – ג׳אול:
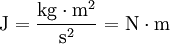
- תדירות – הרץ:
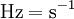
קבועים
- גודל תאוצת הכובד בקרבת כדה״א:
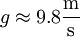
תזכורות ונוסחאות
- מכפלה וקטורית:
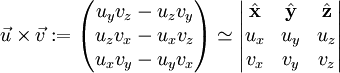
- גרדיאנט:
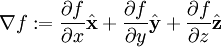
- דיברגנץ:
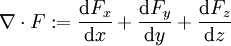
- רוטור/קרל:
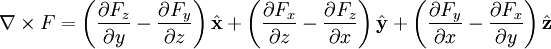
- לפלסיאן:
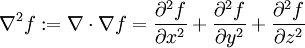
קואורדינטות
עבור ![x,y,z\in(-\infty,\infty)\ \and\ r,\rho\in[0,\infty)\ \and\ \theta\in(-\pi,\pi]\ \and\ \varphi\in\left[-\frac\pi2,\frac\pi2\right]](/images/math/a/1/2/a12b7d1cdf93dd105c1b4fc98cc545ad.png) קואורדינטות כפונקציות של הזמן מתקיים:
קואורדינטות כפונקציות של הזמן מתקיים:
| מ־↓ ל־← | קרטזיות | גליליות | כדוריות |
|---|---|---|---|
| קרטזיות | 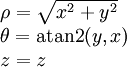
|
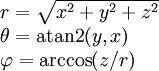
| |
| גליליות | 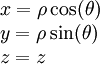
|
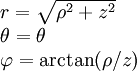
| |
| כדוריות | 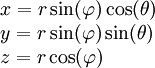
|
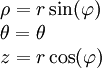
|
כאשר ![\mbox{Im}(\arctan)=\left[-\frac\pi2,\frac\pi2\right]](/images/math/d/7/b/d7bc4621d3333c448be8977cbed722bd.png) ו־
ו־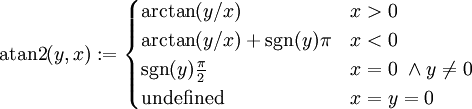 .
.
כמו כן, 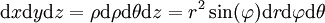 .
.
קינמטיקה
-
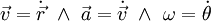 .
. - תנועה במהירות קבועה:
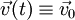 . אזי
. אזי 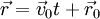 .
. - תנועה בתאוצה קבועה:
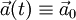 . אזי
. אזי 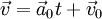 ו־
ו־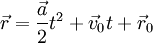 .
. - תנועה בגודל מהירות קבוע:
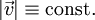 . זה קורה אם״ם
. זה קורה אם״ם 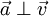 .
. - תנועה כללית במעגל: אם תנועת הגוף במעגל המונח על המישור
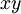 שרדיוסו
שרדיוסו  אזי
אזי 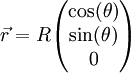 ,
, 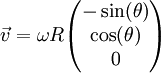 , ו־
, ו־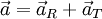 כאשר
כאשר 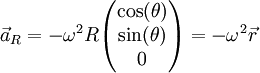 נקראת התאוצה הרדיאלית והיא אחראית לשינוי בכיוון המהירות ו־
נקראת התאוצה הרדיאלית והיא אחראית לשינוי בכיוון המהירות ו־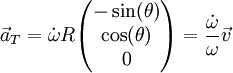 נקראת התאוצה הטנגנטית/משיקית והיא אחראית לשינוי בגודל המהירות. אם נסמן
נקראת התאוצה הטנגנטית/משיקית והיא אחראית לשינוי בגודל המהירות. אם נסמן 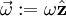 נקבל
נקבל 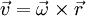 ו־
ו־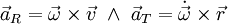 .
.
- תנועה קצובה במעגל: תנועת גוף במעגל כנ״ל כך ש־
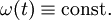 . לכן
. לכן 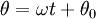 ו־
ו־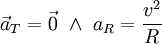 . התאוצה נקראת צנטריפטלית.
. התאוצה נקראת צנטריפטלית.
- התדירות מוגדרת כ־
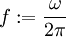 .
. - זמן המחזור מוגדר כ־
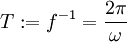 .
.
- התדירות מוגדרת כ־
- תנועה קצובה במעגל: תנועת גוף במעגל כנ״ל כך ש־