תקציר פיזיקה למתמטיקאים, סמסטר ב תשע״ג
מתוך Math-Wiki
להבא, אלא אם צוין אחרת, נסמן:
-
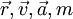 הן המיקום, המהירות, התאוצה והמסה כפונקציה של הזמן
הן המיקום, המהירות, התאוצה והמסה כפונקציה של הזמן 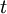 בהתאמה.
בהתאמה. - לכל פונקציה
 של הזמן נסמן
של הזמן נסמן 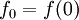 ערך הפונקציה בזמן ההתחלה.
ערך הפונקציה בזמן ההתחלה. - לכל וקטור
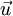 נסמן כ־
נסמן כ־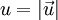 את גודלו וכ־
את גודלו וכ־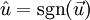 את כיוונו.
את כיוונו.
תוכן עניינים
הקדמה
יחידות
- זמן – שנייה:
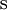
- מרחק – מטר:
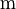
- מסה – קילוגרם:
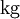
- כוח – ניוטון:
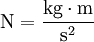
- אנרגיה – ג׳אול:
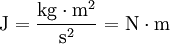
- תדירות – הרץ:
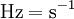
קבועים
- גודל תאוצת הכובד בקרבת כדה״א:
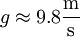
תזכורות ונוסחאות
- מכפלה וקטורית:
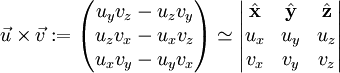
- גרדיאנט:
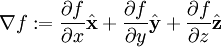
- דיברגנץ:
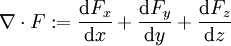
- רוטור/קרל:
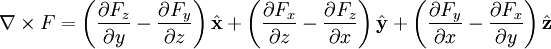
- לפלסיאן:
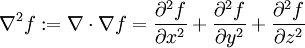
קואורדינטות
עבור ![x,y,z\in(-\infty,\infty)\ \and\ r,\rho\in[0,\infty)\ \and\ \theta\in(-\pi,\pi]\ \and\ \varphi\in\left[-\frac\pi2,\frac\pi2\right]](/images/math/a/1/2/a12b7d1cdf93dd105c1b4fc98cc545ad.png) קואורדינטות כפונקציות של הזמן מתקיים:
קואורדינטות כפונקציות של הזמן מתקיים:
| מ־↓ ל־← | קרטזיות | גליליות | כדוריות |
|---|---|---|---|
| קרטזיות | 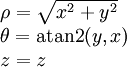
|
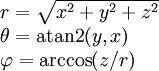
| |
| גליליות | 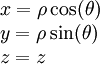
|
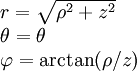
| |
| כדוריות | 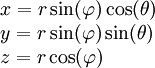
|
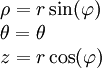
|
כאשר ![\mbox{Im}(\arctan)=\left[-\frac\pi2,\frac\pi2\right]](/images/math/d/7/b/d7bc4621d3333c448be8977cbed722bd.png) ו־
ו־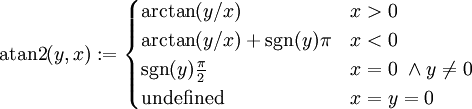 .
.
כמו כן, 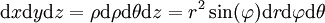 .
.
קינמטיקה
-
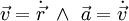 .
. - התדירות הזוויתית:
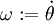 .
. - התנע:
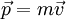 .
. - תנועה במהירות קבועה:
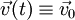 . אזי
. אזי 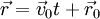 .
. - תנועה בתאוצה קבועה:
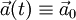 . אזי
. אזי 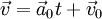 ו־
ו־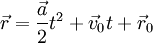 .
. - תנועה בגודל מהירות קבוע:
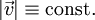 . זה קורה אם״ם
. זה קורה אם״ם 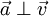 .
. - תנועה כללית במעגל: אם תנועת הגוף במעגל המונח על המישור
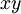 שרדיוסו
שרדיוסו  אזי
אזי 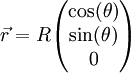 ,
, 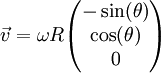 , ו־
, ו־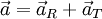 כאשר
כאשר 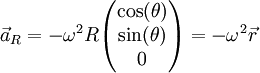 נקראת התאוצה הרדיאלית והיא אחראית לשינוי בכיוון המהירות ו־
נקראת התאוצה הרדיאלית והיא אחראית לשינוי בכיוון המהירות ו־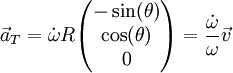 נקראת התאוצה הטנגנטית/משיקית והיא אחראית לשינוי בגודל המהירות. אם נסמן
נקראת התאוצה הטנגנטית/משיקית והיא אחראית לשינוי בגודל המהירות. אם נסמן 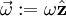 נקבל
נקבל 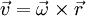 ו־
ו־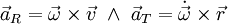 .
.
- תנועה קצובה במעגל: תנועת גוף במעגל כנ״ל כך ש־
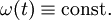 . לכן
. לכן 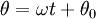 ו־
ו־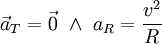 . התאוצה נקראת צנטריפטלית.
. התאוצה נקראת צנטריפטלית.
- התדירות מוגדרת כ־
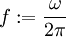 .
. - זמן המחזור מוגדר כ־
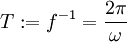 .
.
- התדירות מוגדרת כ־
- תנועה קצובה במעגל: תנועת גוף במעגל כנ״ל כך ש־
מכניקה
חוקי התנועה של ניוטון
- גוף שלא פועלים עליו כוחות ינוע במהירות וכיוון קבועים:
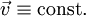 .
. - גוף שמסתו
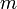 ופועל עליו כוח
ופועל עליו כוח 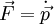 .
. - אם גוף 1 מפעיל כוח
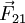 על גוף 2 אז גוף 2 יפעיל כוח
על גוף 2 אז גוף 2 יפעיל כוח 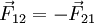 על גוף 1.
על גוף 1.
כוחות נפוצים
- כוח אלסטי: נתון קפיץ שקצה אחד שלו מקובע וקצהו השני נמצא בנקודה
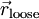 במצב רפוי ובנקודה
במצב רפוי ובנקודה 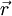 בזמן הנוכחי. אזי מופעל על קצהו השני כוח
בזמן הנוכחי. אזי מופעל על קצהו השני כוח 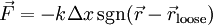 כאשר
כאשר 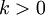 הוא קבוע האלסטיות של הקפיץ ו־
הוא קבוע האלסטיות של הקפיץ ו־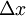 השינוי באורך הקפיץ לעומת המצב הרפוי.
השינוי באורך הקפיץ לעומת המצב הרפוי.
- מתנד (אוסצילטור) הרמוני: מערכת מכנית שבה פועל על גוף נתון כוח פרופורציוני להעתק הגוף ובכיוון מנוגד לו. המערכת הנ״ל היא דוגמה למערכת כזו.
- דוגמה: אם נניח שלקצה ההשני מחובר גוף החופשי לנוע בציר ה־
 וש־
וש־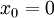 היא הנקודה בה הקפיץ רפוי אזי משוואת הכוחות בציר ה־
היא הנקודה בה הקפיץ רפוי אזי משוואת הכוחות בציר ה־ על הגוף תהא
על הגוף תהא 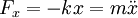 ולכן
ולכן 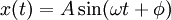 כש־
כש־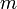 מסת הגוף,
מסת הגוף, 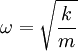 ,
,  היא משרעת התנודה. את המשרעת ואת
היא משרעת התנודה. את המשרעת ואת 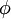 ניתן למצוא עפ״י תנאי התחלה.
ניתן למצוא עפ״י תנאי התחלה.
- כוח מתיחות: בהנתן חוט מתוח שקצה אחד שלו מקובע מופעל על הקצה השני כוח
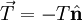 כאשר
כאשר 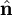 וקטור יחידה בכיוון החוט (כלומר, ככיוון הווקטור המתחיל בקצה הראשון ונגמר בקצה השני), ו־
וקטור יחידה בכיוון החוט (כלומר, ככיוון הווקטור המתחיל בקצה הראשון ונגמר בקצה השני), ו־ גודל הניתן לחישוב. בד״כ מניחים שאורך החוט קבוע.
גודל הניתן לחישוב. בד״כ מניחים שאורך החוט קבוע. - כוח נורמלי: משטח מפעיל כוח
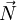 על גוף המונח עליו שכיוונו ניצב לפני המשטח בנקודת המגע בין הגוף למשטח.
על גוף המונח עליו שכיוונו ניצב לפני המשטח בנקודת המגע בין הגוף למשטח. - כוח הכובד: בקרבת כדה״א מופעל כוח הגרביטציה
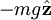 כאשר
כאשר 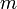 מסת הגוף ו־
מסת הגוף ו־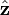 וקטור יחידה בכיוון מעלה.
וקטור יחידה בכיוון מעלה.
חוקי השימור
תהא מערכת ובה הגופים 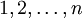 . נסמן את הכוח השקול של הכוחות החיצוניים למערכת הפועלים על גוף
. נסמן את הכוח השקול של הכוחות החיצוניים למערכת הפועלים על גוף 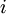 כ־
כ־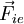 . מסת הגוף
. מסת הגוף 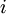 מסומנת
מסומנת 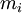 , מיקומו
, מיקומו 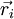 והתנע שלו –
והתנע שלו – 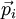 .
.
- המסה הכוללת של המערכת מוגדרת כ־
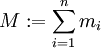 .
. - מרכז המסה של המערכת מוגדר כ־
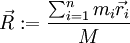 .
. - התנע הכולל של המערכת מוגדר כ־
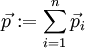 . אם המסות קבועות אז הוא שווה ל־
. אם המסות קבועות אז הוא שווה ל־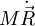 .
. - לפי החוק השלישי של ניוטון
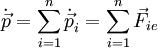 .
. - חוק שימור התנע: אם שקול הכוחות החיצוניים הוא
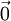 אז
אז 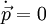 , כלומר התנע הכולל קבוע.
, כלומר התנע הכולל קבוע.
- אם התנע קבוע אז מרכז המסה ינוע במהירות קבועה (בגודל ובכיוון).