הבדלים בין גרסאות בדף "תקציר תורת המספרים, סמסטר א תשע״ג"
מתוך Math-Wiki
(יצירת דף עם התוכן "בקורס זה <math>\mathbb N=\{0,1,2,\dots\}</math> ו־<math>\mathbb N^+=\{1,2,\dots\}</math>. כמו כן, אלא אם צוין אחרת, <math>A^+:=A\cap\math...") |
(אין הבדלים)
|
גרסה מ־21:45, 21 בדצמבר 2012
בקורס זה 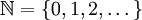 ו־
ו־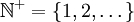 . כמו כן, אלא אם צוין אחרת,
. כמו כן, אלא אם צוין אחרת, 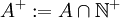 וכל המשתנים והנעלמים שלמים.
וכל המשתנים והנעלמים שלמים.
- משפט פיאנו: קיימת קבוצה בודדה
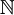 שעבורה יש פונקציה
שעבורה יש פונקציה 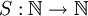 המקיימת את אקסיומות פיאנו:
המקיימת את אקסיומות פיאנו: 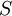 חח״ע,
חח״ע, 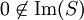 ,
, 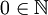 ואם
ואם 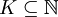 מקיימת
מקיימת 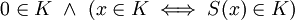 אזי
אזי 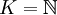 .
. -
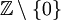 מחולק לשלוש קבוצות: יחידות –
מחולק לשלוש קבוצות: יחידות – 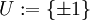 , ראשוניים –
, ראשוניים – 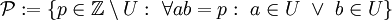 ופריקים –
ופריקים – 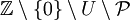 .
. - לכל
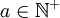 ו־
ו־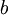 קיים זוג יחיד של שארית
קיים זוג יחיד של שארית 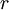 ומנה
ומנה 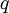 כך ש־
כך ש־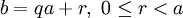 .
. - המשפט הבסיסי של האתריתמטיקה: כל מספר ב־
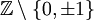 ניתן לפירוק יחיד (עד כדי סדר ההכפלה) של גורמים ראשוניים.
ניתן לפירוק יחיד (עד כדי סדר ההכפלה) של גורמים ראשוניים. - למת אוקלידס: יהי
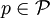 . אם
. אם 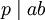 אז
אז 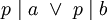 .
. - יהיו
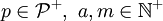 . נסמן
. נסמן 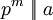 אם
אם 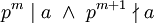 .
. - נניח ש־
 ו/או
ו/או 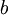 שונים מ־0. אזי קיים
שונים מ־0. אזי קיים 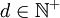 יחיד (הנקרא מחלק משותף מקסימלי של
יחיד (הנקרא מחלק משותף מקסימלי של 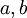 ומסומן
ומסומן 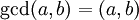 ) עבורו
) עבורו 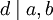 ואם
ואם 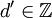 כך ש־
כך ש־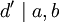 אזי
אזי 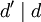 .
. - אם
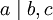 אזי
אזי 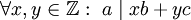 .
. -
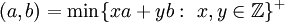 .
. -
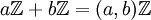 .
. - אם
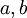 זרים ו־
זרים ו־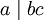 אזי
אזי 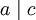 .
. - אם
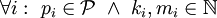 אזי
אזי 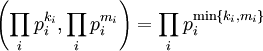 .
. - אלגוריתם אוקלידס: נניח
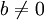 ונרצה לחשב
ונרצה לחשב 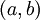 כאשר
כאשר 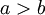 . אם
. אם 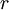 שארית החלוקה של
שארית החלוקה של  ב־
ב־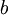 אזי
אזי 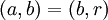 . נמשיך כך עד שנקבל
. נמשיך כך עד שנקבל 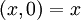 . ניתן להעזר באלגוריתם גם כדי לפתור את
. ניתן להעזר באלגוריתם גם כדי לפתור את 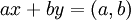 : נסמן
: נסמן 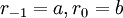 ולכן בתהליך החישוב של
ולכן בתהליך החישוב של 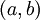 עם האלגוריתם נקבל
עם האלגוריתם נקבל 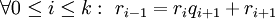 כאשר
כאשר 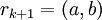 . לפיכך:
. לפיכך: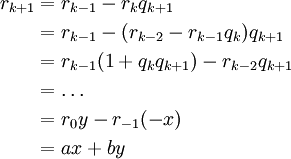
- משוואה דיאופנטית ב־2 משתנים: נרצה לפתור
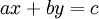 כאשר
כאשר 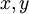 משתנים והשאר קבועים. נחלק למקרים:
משתנים והשאר קבועים. נחלק למקרים:
-
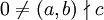 : אין פתרון.
: אין פתרון. -
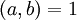 : ניתן לפתור
: ניתן לפתור 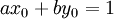 ע״י אלגוריתם אוקלידס (כמפורט בהמשך הסעיף). הפתרון הכללי הוא
ע״י אלגוריתם אוקלידס (כמפורט בהמשך הסעיף). הפתרון הכללי הוא 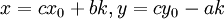 לכל
לכל  .
. -
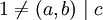 : נחלק את אגפי המשוואה ב־
: נחלק את אגפי המשוואה ב־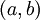 ונקבל משוואה חדשה מהמקרה הקודם.
ונקבל משוואה חדשה מהמקרה הקודם.
- אם בפרט
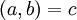 אז ניתן לפתור גם באמצעות אלגוריתם אוקלידס.
אז ניתן לפתור גם באמצעות אלגוריתם אוקלידס.
- אם בפרט
-
- נאמר ש־
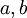 חופפים מודולו
חופפים מודולו 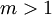 (ונסמן
(ונסמן 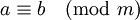 ) אם
) אם 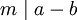 .
.  מגדיר יחס שקילות כאשר
מגדיר יחס שקילות כאשר ![\bar a=[a]=a+m\mathbb Z](/images/math/6/9/9/699de2c687a3c00ec3aa45430b050d3a.png) מחלקת השקילות של
מחלקת השקילות של  ו־
ו־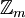 קבוצת מחלקות השקילות.
קבוצת מחלקות השקילות. - אם
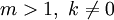 ו־
ו־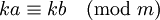 אז
אז 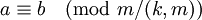 .
. - יהי
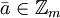 .
. 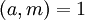 אם״ם
אם״ם 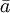 הפיך. ניתן למצוא את ההופכי ל־
הפיך. ניתן למצוא את ההופכי ל־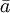 ע״י פתירת
ע״י פתירת 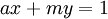 , ואז
, ואז 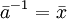 .
. -
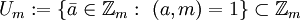 .
. - פונקציית אוילר היא
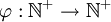 עבורה
עבורה 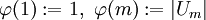 .
. - משפט אוילר: אם
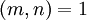 אז
אז 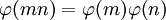 .
. - מערכת מלאה מודולו m היא קבוצה
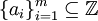 עבורה
עבורה 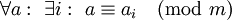 . קיים
. קיים 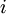 כנ״ל יחיד לכל
כנ״ל יחיד לכל  . באופן שקול, המערכת מלאה מודולו
. באופן שקול, המערכת מלאה מודולו 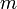 אם
אם 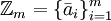 .
. - אם
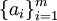 מלאה מודולו
מלאה מודולו 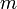 ,
, 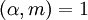 ו־
ו־ שלם אזי
שלם אזי 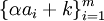 מלאה מודולו
מלאה מודולו 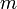 .
. - מערכת מצומצמת מודולו m היא קבוצה
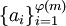 כך ש־
כך ש־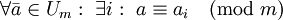 .
. - אם
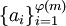 מצומצמת מודולו
מצומצמת מודולו 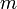 ו־
ו־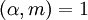 אז
אז 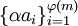 מצומצמת מודולו
מצומצמת מודולו 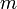 .
.