הבדלים בין גרסאות בדף "תרגול 10 תשעז"
| שורה 1: | שורה 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===יחסי שקילות=== | ===יחסי שקילות=== | ||
הגדרה: תהא A קבוצה ו-R יחס עליה. R יקרה יחס שקילות אם הוא | הגדרה: תהא A קבוצה ו-R יחס עליה. R יקרה יחס שקילות אם הוא | ||
גרסה מ־08:54, 20 ביוני 2017
יחסי שקילות
הגדרה: תהא A קבוצה ו-R יחס עליה. R יקרה יחס שקילות אם הוא
- רפלקסיבי
- סימטרי
- טרנזיטיבי
סימון מקובל:
אם R יחס שקילות מסמנים גם 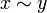 עבור
עבור 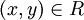
וכן נסמן 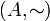 את הקבוצה עם יחס השקילות
את הקבוצה עם יחס השקילות
דוגמא נוספת:
נגדיר יחס שקילות R על 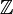 ע"י
ע"י 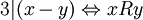
טענה: R אכן יחס שקילות
הוכחה:
1. רפלקסיביות - נניח 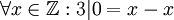 לכן
לכן 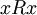
2. סימטריות - נניח 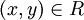 אזי
אזי 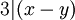 ולכן גם
ולכן גם 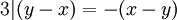
3. טרנזיטיביות - נניח ![[(x,y)\in R] \and [(y,z)\in R]](/images/math/0/b/e/0be7ba4e28716aaf8c19a241b4c93189.png) אזי
אזי 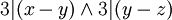 ולכן גם
ולכן גם 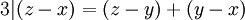
הגדרה: תהא A קבוצה. חלוקה של A היא חלוקה של A לקבוצות זרות. באופן פורמלי קיימות תת קבוצות 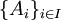 כך ש:
כך ש:
-
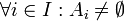
-
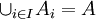 כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה
כלומר האיחוד של כל תתי הקבוצות שווה לקבוצה כולה - הקבוצות
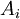 הן זרות זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (
הן זרות זו לו = החיתוך בין כל שתי תתי קבוצות הוא ריק (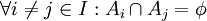 )
)
הגדרה:
יהא R יחס שקילות על A אזי
- לכל
 מוגדרת מחלקת השקילות של x להיות
מוגדרת מחלקת השקילות של x להיות ![\bar{x}=[x]_R:=\{y\in A | (x,y)\in R\}](/images/math/3/e/c/3ec2682e1e1f10cf21a983d1a44b2f96.png)
- קבוצת המנה מוגדרת
![A/R := \{ [x]_R | x\in A\}](/images/math/4/c/5/4c58650f9531733c432c54f74881db01.png)
למשל, בדוגמא הראשונה 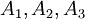 הן מחלקות השקילות. קבוצת המנה היא
הן מחלקות השקילות. קבוצת המנה היא 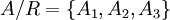
בדוגמא השניה מחלקת השקילות של 0 היא ![[0]_R=\{ 0 \pm 3 \pm 6 \dots \}](/images/math/2/5/9/2598a70b2805b479700f0e7e2dceff56.png) וקבוצת המנה היא
וקבוצת המנה היא
![\mathbb{Z}/R= \{[0]_R,[1]_R,[2]_R\}](/images/math/b/0/6/b06f29fa198c69e36280452ef86cb9e9.png) (כלומר כל השאריות האפשריות בחלוקה ב-3).
(כלומר כל השאריות האפשריות בחלוקה ב-3).
משפט: יהא R יחס שקילות על A אזי
- לכל
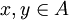 מתקיים
מתקיים ![[x]=[y]](/images/math/6/3/b/63be84aae0ca1995af2d779096090fdc.png) או
או ![[x]\cap [y] =\phi](/images/math/2/8/5/285cdd0729559197bf11c30df83a2f8f.png) (כלומר מחלקות השקילות זרות)
(כלומר מחלקות השקילות זרות) -
![A=\bigcup_{[x]\in A/R}[x]](/images/math/3/3/2/3323ab7c4ddf604cede7985587f3c401.png) כלומר (איחוד מחלקות השקילות תתן את כל A)
כלומר (איחוד מחלקות השקילות תתן את כל A)
הערה: זה בדיוק אומר שמיחס שקילות ניתן להגיע לחלוקה של A
מסקנה:
תהא A קבוצה אזי יש התאמה { יחס שקילות על A }
יחס שקילות על A }
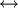 {חלוקות של A}
{חלוקות של A}
חידוד: מהותו העיקרית של יחס שקילויות הוא לשים לב לשקילות מסוימת בין אברים שונים (כמו שיוויון) ולצמצם את החזרות המיותרות על ידי קיבוץ כל האיברים השקולים לקבוצה אחת.